群れの集団動力学
〜マガンの紐運動の解析〜

人間はもちろんとして、生物・非生物を問わず、集団が個とは本質的に異なる挙動を示す例は枚挙にいとまがありません。
こうした「集団モードの発現」に関連して、鳥などの群れの集団動力学の計測とその数理モデルの研究を行っています。

Reference:
Spatiotemporal Dynamics of Skeins of Wild Geese, Yoshinori Hayakawa, Europhysics Letters 89, 48004 (2010).

複雑ネットワークの自己組織
〜協調と非協調エージェントが共存する系のネットワーク形成〜

近年、複雑ネットワークの研究が各方面で活発に行われています。例えば、社会の中のどのようにコミュニティーが形成されるのか、そしてその安定性や動的な変化は、興味深い問題です。
意見や嗜好などを周囲と「合わせる」タイプのエージェントと、その反対の性質を持つものが「共生」するようなシステムで、どのようなネットワークが形成されるのか、シミュレーションと理論によって研究しています。

Reference:
Coevolutionary networks with homophily and heterophily, Daichi Kimura and Yoshinori Hayakawa, Physical Review E 78, 016103 (2008).

形の自己組織
〜金平糖の角の形成〜

生き物に限らず、非平衡な系では成長に伴って興味深い「形」が自発的に現れる例が沢山あります。美しい雪の結晶はその典型的な例です。
こうした例として、金平糖にどのように、そしてどうして角が生えるのかについて、実験と数理の両面からアプローチしています。

Reference:
Shape Selection of Kompeitoh, Isamu Sakai and Yoshinori Hayakawa, J. Phys. Soc. Jpn. 75, 104802 (2006).

文長分布の対数正規性
〜文生成に隠れた統計性〜

我々が文章を書くときに、「あまり長くなり過ぎないように」くらいの注意は払うかもしれませんが、それぞれの文の長さ（文字数や単語数）は、全く書き手に委ねられているはずです。ところが、ネットなどから沢山の文を収集して、その長さを調べると、対数正規分布と呼ばれる、単純な分布によく従っていることが分かりました。つまり、我々は無意識に、ある種の共通のルールに従って文を「産出」しているらしいのです。

Reference:
Lognormality of the Distribution of Japanese Sentence Lengths, Sho Furuhashi and Yoshinori Hayakawa, J. Phys. Soc. Jpn. 81, 034004 (2012).

非線形弾性と亀裂の不安定
〜ゴム膜の波打つ裂け目〜

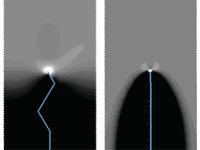引き伸ばされたゴムの膜が「ゆっくりと」割れるようにある細工を施してから、風船を割るように切れ目を入れてやると、条件によって、亀裂が大きく波打つことを発見しました。何故、亀裂はジグザグになるのか、その理由を探っています。

Reference:
Oscillatory instability in slow crack propagation in rubber under large deformation, Daiki Endo,Katsuhiko Sato and Yoshinori Hayakawa, Physical Review E 86, 016106 (2012).

群れサイズの調整メカニズム
〜鳥の群れの大きさはどのように決まるのか〜

宮城県北部で冬場によく見られるマガンの編隊を沢山撮影し、それぞれの編隊が何羽の個体で構成されているかを調べると、ある簡単な分布関数でよく表せることが分かりました。観察事実に基づいて、群れの合体と分裂を表現する数理モデルを立てることによって、動物の群れの大きさがどのように自律的（あるいは偶然的に）調整されているのかを調べています。

Reference:
Group-size distribution of skeins of wild geese, Yoshinori Hayakawa and Sho Furuhashi, Physical Review E 86, 031924 (2012).

群れの集団動力学
〜ゾウリムシの「交通渋滞」〜

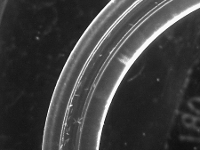交通渋滞は、必ずしも、道路上で発生するだけでなく、走性を持つ生物の集合や離散も、渋滞の一種として考えることができます。
ゾウリムシを細いリング状のチューブの中に閉じ込めると、その中で「渋滞」が観察されますが、そのメカニズムは、高速道路の渋滞とは質的に異なることが分かりました。
Reference:
Adaptation-induced collective dynamics of a single-cell protozoan, Maiko Ogata, Tsuyoshi Hondou, Yoshinori Hayakawa, Yoshikatsu Hayashi and Ken Sugarawa, Physical Review E 77, 011917 (2008).

大変形する流体の動力学
〜ハチミツのコイル化のモデル〜

境界が自由に運動・変形できる粘性流体の、多様な運動を記述する方法の開発と、その数値シミュレーションに取り組んでいます。

Reference:
Bending-filament model for the buckling and coiling instability of a viscous fluid rope, Shin-ichiro Nagahiro and Yoshinori Hayakawa, Physical Review E 78, 025302R (2008) .
Model for Coiling and Meandering Instability of Viscous Threads, Shin-ichiro Nagahiro and Yoshinori Hayakawa, Journal of Physical Society of Japan 78, 124402 (2009).

流体と物体の衝突の数理
〜石の水切りのモデル〜

河原で石の水切りをした経験を持つ人は多いのではないでしょうか。世界記録として、50回以上石を跳躍させた例もあるそうです。
この日常的な現象について、流体力学に基づいた数値シミュレーションと、モデル方程式による解析を行い、実験的に知られていた石が最もよく跳ねるための入射角（「マジックアングル」）などを定量的に説明することに成功しました。

Reference:
Theoretical and numerical approach to “magic angle” of stone skipping, S. Nagahiro and Y. Hayakawa, Physical Review Letters 94, 174501 (2005).