 フラクタル分布の一般化次元
フラクタル分布の一般化次元
 フラクタル分布の一般化次元
フラクタル分布の一般化次元
Rnの有界な領域上で定義された測度 μ(x)>0 (x∈X⊂Rn) を考えよう. ただし,μ(X)=1とする. このとき,μのサポートXそれ自体がフラクタル集合であっても構わない. Xを覆うサイズδのボックスの集合{Bi}上の測度を μ(Bi)と表記し,全てのボックスに渡る以下の総和を定義する.
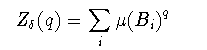 (3-1)
(3-1)
このZδ(q)によって,分布のq次モーメントに関係したフラクタル 次元
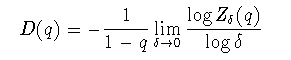 (3-2)
(3-2)
事実,Zδ(0)が集合Xを覆うために必要な箱の数に他ならないことに 注意すると, limδ→0 - logZδ(0)/logδ, すなわちD(0)はμのサポートのボックス次元を与える.
また,D(1)は,q→1の極限を取ることによって
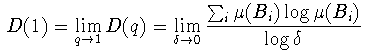 (3-3)
(3-3)
自己相似図形ではD(q)がqに依らず一定となるが, μがさらに複雑な構造を持つ場合にはD(q)がqに依存する. このようなμはマルチフラクタル(multi-fractal)と呼ばれ, D(q)はqの単調減少関数となる.
 fーαスペクトル
fーαスペクトル
マルチフラクタルな集合は,以下で述べるように,異なるフラクタル次元が 分布しているような集合とみなすことができる. まず,測度の局所的な特異性を表わす指標として 0<α<∞であるような指数αを導入する. ここで,ボックスのサイズδ=|Bi|について局所的なスケーリング
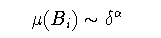 (3-4)
(3-4)
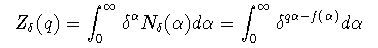 (3-5)
(3-5)
δ→0では,この積分の値は指数部分が最大となるようなα での寄与が支配的になると考えられるため,
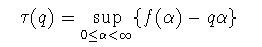 (3-6)
(3-6)
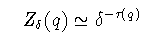 (3-7)
(3-7)
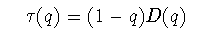 (3-8)
(3-8)
ここで,f,αの微分可能性と,f(α)が αの凸関数であることを仮定する. f(α)ーqαが極大となる条件から
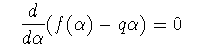 (3-9)
(3-9)
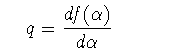 (3-10)
(3-10)
また,τ(q)=f(α(q))ーqα(q)をqで微分して
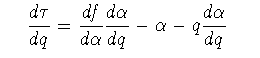
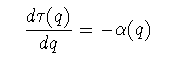 (3-11)
(3-11)
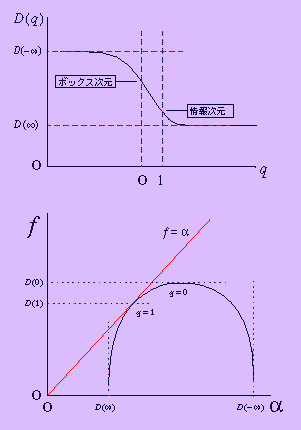
これらの一連の変換は分配関数Z(q)から,ヘルムホルツの自由エネルギー τ(q)を求め,ルジャンドル変換によって内部エネルギーαと エントロピーfに変数変換する統計力学の手続きそのものである. 一般に分布(測度)の局所的なスケーリング関係(3-4) から出発してf(α)を求めるのは困難であるので, τ(q)を経て上記の手順によってf(α(q))を求めることが多い.
fのα依存性はfーαスペクトルと呼ばれており,カオス アトラクタの構造のような複雑な確率分布を特徴付ける際に使われる. fーαスペクトルの一般的特徴を以下にまとめる(図を参照).