拡散モデル
このページでは、生成AIで使われている拡散モデルについて、その動作原理について考えてみる。(書きかけ)
ランジュバン方程式で記述される拡散とその逆過程
O−U過程を表すランジュバン方程式 $$ \frac{d x(t)}{dt} = -B x + \xi(t) $$ を考えてみよう。ここで、揺動項 $\xi$の平均は$0$、自己相関を$R$とする。
ここの箇所は Reverse-time diffusion equation models (Anderson, 1982)の5節のあたりを参照のこと。
このプロセスに従って$x$が変動しているときに、 異なる時刻 $t$ と $s$ (ただし $t \lt s$)を考え、時刻 $s$ で状態が $x_s$ であるような「経路」に注目してみる。 そのような条件付きの確率密度は、コルモゴロフの後退方程式(Kolmogorov backward equations) $$ - \frac{\partial p(x_s,s|x_t,t)}{\partial t} = - B x_t \frac{\partial p(x_s,s|x_t,t) }{\partial x_t} + \frac{R}{2} \frac{\partial^2 p(x_s,s|x_t,t)}{\partial {x_t}^2} \tag{1} $$ によって記述される。
一方で、密度関数$p(x_t,t)$の初期条件が与えられると、その後の分布の時間発展はフォッカー・プランク方程式(コルモゴロフの前進方程式とも呼ばれる) $$ \frac{\partial p(x_t,t)}{\partial t} = B \frac{\partial \left\{x_t p(x_t,t) \right\}}{\partial x_t} + \frac{R}{2} \frac{\partial^2 p(x_t,t)}{\partial {x_t}^2} \tag{2} $$ に従う。
以上を踏まえて、 時刻$t$で$x_t$を通過し、かつ、時刻$s$で$x_s$に至るような確率分布、すなわち $$ p(x_t, t, x_s, s) $$ の時間発展がどのような式で表されるかを考える。 結合確率と条件付き確率の関係から、 $$ p(x_t, t, x_s, s) = p(x_s,s|x_t,t) p(x_t,t) $$ であるから、 $$ p(x_s,s|x_t,t) = \frac{p(x_t, t, x_s, s)}{p(x_t,t)} $$ とおき直して、式(1)に代入する。 得られた式の$\frac{\partial p(x_t,t)}{\partial t}$のところに、式(2)の右辺を代入すると、 $p(x_s,s|x_t,t)$と$p(x_t,t)$、およびそれらの微分を含んだ方程式が得られる。
sympyを使ってこれを計算するコードの例を以下に示す。
ここで、少々紛らわしいが、コード中の記号を区別するため、$p(x_t, t, x_s, s)$をF、$p(x_t,t)$にPの変数名を割り当てていることに注意。
from sympy import *
x_t,x_s = symbols('x_t x_s')
t,s = symbols('t s')
B,R = symbols('B R')
# P(xs, s, xt, t)
F = Function('F')(x_s,s,x_t,t)
# P(xs, s | xt, t)
Q = Function('Q')(x_s,s,x_t,t)
# P(xt, t)
P = Function('P')(x_t,t)
Q = F/P
BKE = diff(Q,t) - B*x_t*diff(Q,x_t) + R/2*diff(Q,x_t,x_t)
DPDT = B * diff(x_t*P,x_t) + R/2*diff(P,x_t,x_t)
res = BKE.subs(Derivative(P, t), DPDT)
res = simplify(res * P)
print('RESULT=')
print(res)
print('LATEX=')
print(latex(res))
実行すると、以下のような結果が得られる。これを0とおいた式が求めたい方程式である。 $$ - B x_{t} \frac{\partial}{\partial x_{t}} F{\left(x_{s},s,x_{t},t \right)} - B F{\left(x_{s},s,x_{t},t \right)} - \frac{R F{\left(x_{s},s,x_{t},t \right)} \frac{\partial^{2}}{\partial x_{t}^{2}} P{\left(x_{t},t \right)}}{P{\left(x_{t},t \right)}} + \frac{R F{\left(x_{s},s,x_{t},t \right)} \left(\frac{\partial}{\partial x_{t}} P{\left(x_{t},t \right)}\right)^{2}}{P^{2}{\left(x_{t},t \right)}} + \frac{R \frac{\partial^{2}}{\partial x_{t}^{2}} F{\left(x_{s},s,x_{t},t \right)}}{2} - \frac{R \frac{\partial}{\partial x_{t}} F{\left(x_{s},s,x_{t},t \right)} \frac{\partial}{\partial x_{t}} P{\left(x_{t},t \right)}}{P{\left(x_{t},t \right)}} + \frac{\partial}{\partial t} F{\left(x_{s},s,x_{t},t \right)} $$ 見かけは少々煩雑だが、$x_t$についての微分をまとめるなどして、式をさらに整理すると、 $$ \frac{\partial F}{\partial x_t} - \frac{\partial}{\partial x_t} \left[ \left( B x_t + R \frac{\frac{\partial P}{\partial x_t}}{P} \right) F \right] + \frac{R}{2} \frac{\partial^2 F}{\partial {x_t}^2} $$ となっていることが分かる。
元の記法に戻して、改めて方程式の形にすると、 $$ - \frac{\partial p(x_s,s,x_t,t)}{\partial x_t} = - \frac{\partial}{\partial x_t} \left[ \left( B x_t + R \frac{\frac{\partial p(x_t,t)}{\partial x_t}}{p(x_t,t)} \right) p(x_s,s,x_t,t) \right] + \frac{R}{2} \frac{\partial^2 p(x_s,s,x_t,t)}{\partial {x_t}^2} $$ を得る。
上の式は、$p_s(x_t,t) = \int p(x_s,s,x_t,t) d x_s$ と周辺化した確率についても成立するのは明らかである。 加えて、時間の向きを反転させ、$\tau = t_0 -t$とおくと、 元々のランジュバン方程式で時間を時間を反転させたときの分布関数の時間発展を記述する式 $$ \frac{\partial p_s(x_\tau,\tau)}{\partial \tau} = - \frac{\partial}{\partial x_\tau} \left[ \left( B x_t + R \frac{\frac{\partial p(x_\tau,\tau)}{\partial x_\tau}}{p(x_\tau,\tau)} \right) p_s(x_\tau,\tau) \right] + \frac{R}{2} \frac{\partial^2 p_s(x_\tau,\tau)}{\partial {x_\tau}^2} \tag{3} $$ が得られる。 対数微分を使えば、右辺の微分のところは $$ \frac{\frac{\partial p(x_\tau,\tau)}{\partial x_\tau}}{p(x_\tau,\tau)} = \frac{\partial \log p(x_\tau,\tau)}{\partial x_\tau} $$ と書ける。
これを眺めると、揺動の自己相関が$R$で、かつ、ドリフト項が $$ g(x_\tau) = B x_\tau + R \frac{\partial \log p(x_\tau,\tau)}{\partial x_\tau} $$ であるようなランジュバン方程式、すなわち $$ \frac{d x(\tau)}{d \tau} = g(x(\tau)) + \xi $$ で「前進」する系とも見なせる。 ただし、$\log p(x_\tau,\tau)$の微分があらかじめ分かっていない限り、この方程式を実際に「動かす」ことはできない。
一次元の拡散モデル
確率密度$p(x,0)$でサンプルされた$N$個の粒子を調和ポテンシャル中で$T$の間拡散させる問題を考える。 $i$番目の粒子の状態を$x_i(t)$とすると、それぞれの粒子を $$ \frac{dx_i}{dt} = -B x_i + \xi $$ によって時間発展させるわけである。 いつものとおり $\langle \xi(t) \rangle=0$, $\langle \xi(t) \xi(s) \rangle = R \delta(t-s)$とする。 こちらのページで述べたように、$T$が十分大きければ、$p(x,T)$は平均が0のガウス分布へと近づくことになる。
では、$t=T$から時間を反対回しに$x$を変化させる過程を考えてみる。ここで、改めて$\tau = T-t$とすると、 前節で見たとおり、その過程をなぞるには $$ \frac{d x_i(\tau)}{d \tau} = B x_i(\tau) + R \frac{\partial \log p(x_i(\tau),\tau)}{\partial x_i} + \xi \tag{4} $$ に従って$\tau =0$から$T$まで粒子を運動させればよい。
ここで、多量の画像などのデータが与えられているような状況を想定しつつ、 問題設定として、確率密度$p(x,0)$に従うデータ集合$\{x_i\}$のみが与えられていて、$p(x,0)$の関数形そのものは未知である場合を考えてみよう。
通常のDenoising Score Matchingの評価関数は、時間方向に積分した量で定義されているが、 このページの例では、(計算リソースの節約のため)各時間ステップ$\tau$事に逐次的に$E(\tau)$を最小化する方法で試してみる。
そんな場合でも、データ点$x_i$から出発して、順方向にランジュバン方程式を解くことで、$\tau = T - t$での値$x_i(\tau)$は得ることはできる。 さらに、$x_i(\tau)$での$\frac{\partial \log p(x,\tau)}{\partial x}$を知ることができれば、 二乗距離をサンプルで重みづけた平均量 $$ E = \frac{1}{N} \sum_i^N \left( s(x_i(\tau), \tau) - \frac{\partial \log p(x_i,\tau)}{\partial x_i} \right)^2 $$ を最小化するような近似関数(スコア関数と呼ばれている)$s(x,\tau)$ を求め、 一般の$x$については、$\frac{\partial \log p(x,\tau)}{\partial x}$の代用として、この$s(x,\tau)$を用いてみてはどうだろうか。
うまいことには、こちらのページで述べたとおり、調和ポテンシャル中の拡散(O-U過程)では、$p(x,0) = \delta(x-x_0)$(つまり$x_0$から出発した粒子)からの分布関数の発展は $$ G(x,t) = \sqrt{\frac{B}{2 \pi D \left( 1 - e^{-2 B t}\right)}} \exp\left[ -\frac{B (x - x_0 e^{-B t})^2}{2 D \left( 1 - e^{-2 B t}\right)} \right] \tag{5} $$ ($D=R/2$)であることがあらかじめ分かっているので、この対数を取って$x$で微分することで $$ \frac{\partial \log p(x,\tau)}{\partial x} = -\frac{B (x - x_0 e^{-B (T-\tau)})}{D \left( 1 - e^{-2 B (T-\tau)}\right)} $$ となる。
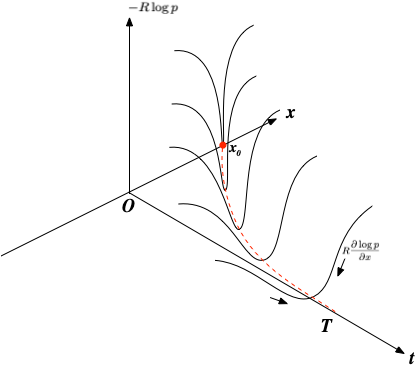
一つのサンプルについて、状態に応じた復元力が作用しながら時間を遡るイメージ図。 式(4)は、多数のサンプルのこうした効果の合算によって生成される複雑なポテンシャル場の中のランダムウォークと捉えることもできる。
であるから、具体的な評価関数を $$ E = \frac{1}{N} \sum_i^N \left( s(x_i, \tau) + \frac{B (x_i - x_i(0) e^{-B (T-\tau)})}{D \left( 1 - e^{-2 B (T-\tau)}\right)} \right)^2 $$ として、ニューラルネットワークで関数のフィッティングを行うことで、 関数$s(x_i, \tau)$のパラメータを決められるようになるはずだ。
この考えでうまく働くかどうか確認するため、簡単な例として、2つの矩形状の分布から出発して粒子を拡散させ、その後、上記のプロセスによって$\tau=T$(すなわち$t=0$)まで逆回しに拡散させる様子をシミュレーションしてみよう。
以下のコード中では、順方向の拡散には変数名 x、逆方向は yを使って区別している。
スコア関数のフィッティングには、簡単な二層のニューラルネット(パーセプトロン)を用いた。
# Y. Hayakawa
# CDS, Tohoku Univesity
import matplotlib.pyplot as plt
import random
import math
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras import optimizers
R=1
B=1
DT=1.0/64
T=1
R2=math.sqrt(R)
D=R/2
# learning model for score function
model = Sequential()
model.add(Dense(16, input_dim=1, activation='relu', use_bias=True))
model.add(Dense(1, use_bias=True, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='Adam')
N=2000
# generate sample
x0s = []
for i in range(N):
if i%2==0:
x = random.uniform(-2,-1)
else:
x = random.uniform(1,2)
x0s.append(x)
x0s = np.array(x0s)
# forward diffusion
SQRTDT=math.sqrt(DT)
def fwd_diffuse(x0,t1):
x = x0
t = 0
while t<t1:
dx = -B*x*DT + R2*random.gauss(0,1)*SQRTDT
x = x + dx
t = t + DT
return x
y0s = []
for i in range(N):
x0 = x0s[i]
y = fwd_diffuse(x0,T)
y0s.append(y)
y0s = np.array(y0s)
ys = np.copy(y0s)
t = T
while t>0:
print("TAU=",T-t)
# training score
dlogp_train = [ ]
x_train = [ ]
for i in range(N):
x0 = x0s[i]
x = fwd_diffuse(x0,t)
dlogp = - B *(x - x0*math.exp(-B*t))/(D*(1-math.exp(-2*B*t)))
x_train.append(x)
dlogp_train.append(dlogp)
x_train = np.array(x_train)
dlogp_train = np.array(dlogp_train)
model.fit(x_train, dlogp_train, epochs=20, verbose=0)
# reverse diffusion
score = model.predict(ys, verbose=0)[:,0]
dy = (B*ys + R*score)*DT + R2*np.random.normal(0,1,N)*SQRTDT
ys = ys + dy
t = t - DT
fig = plt.figure()
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)
ax1.hist(x0s,bins=20,density=True)
ax1.set_xlabel('x0')
ax1.set_ylabel('p(x0)')
ax1.set_xlim(-3,3)
ax2.hist(y0s,bins=20,density=True)
ax2.set_xlabel('y0')
ax2.set_ylabel('p(y0)')
ax2.set_xlim(-3,3)
ax3.hist(ys,bins=20,density=True)
ax3.set_xlabel('y_T')
ax3.set_ylabel('p(y_T)')
ax3.set_xlim(-3,3)
ax4.scatter(ys,score)
ax4.set_xlabel('y')
ax4.set_ylabel('score')
ax4.set_xlim(-3,3)
plt.show()
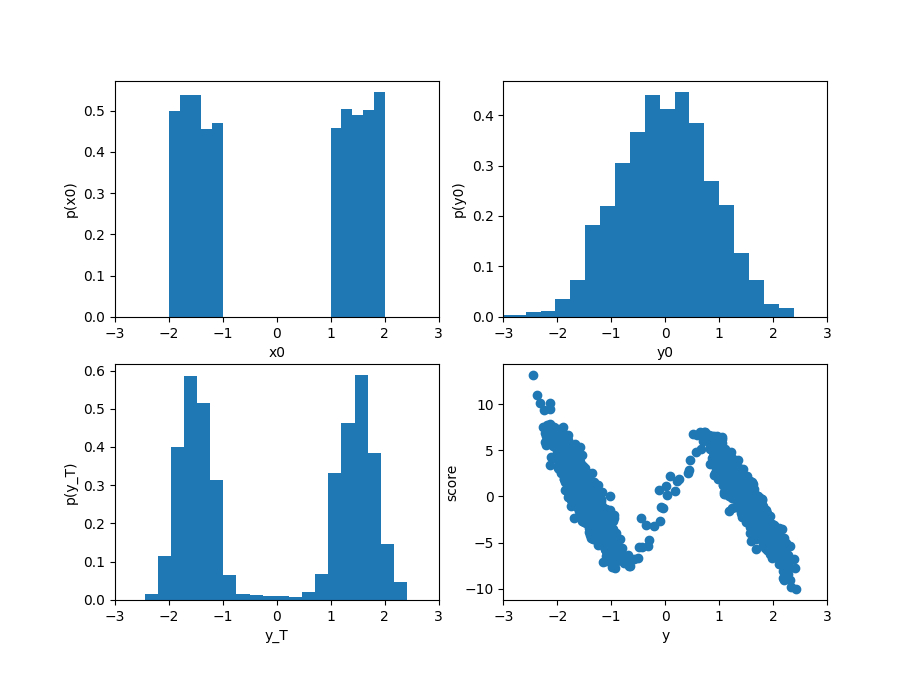
この例ではサンプル数は$N=2000$としており、左上が初期の分布$p(x,t=0)$になる。
これを差分ステップ DT で Tまで拡散させる。拡散後の分布がグラフ右上で、原点の周りでベル型になっていることが判る。
そこから出発して、時間を逆向きに拡散し$\tau=T$での分布の様子がグラフ左下である。初期分布とは多少異なるものの、二峰の分布が再構成されている。
その時点でのスコア関数の様子が右下のグラフである。
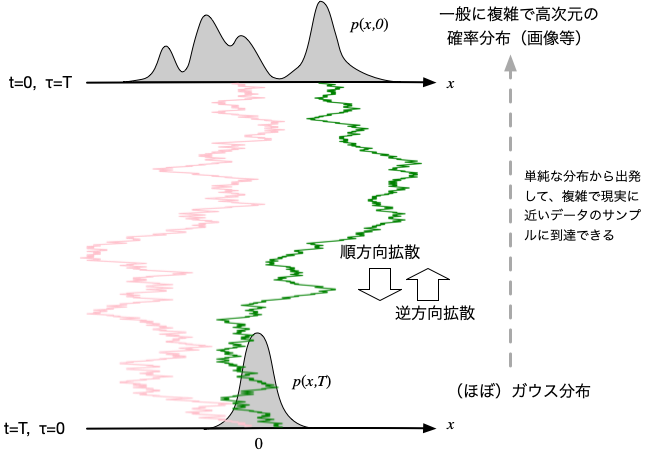
ここで、現実世界のデータを沢山収集し、それを初期値 $\{x_i(0)\}$ として上記の順方向の拡散を行ったとすると、$t=T$で、データは原点付近に単純なガウス分布として現れる。 反対に、ガウス分布から出発して、現実のデータセットから生成したスコア関数$s(x,t)$を用いつつ逆方向に拡散させると、現実に近い確率分布でデータ点をサンプリングできる可能性がある。
事実、データセットとして画像を用いることで、現実に酷似した画像を確率的に生成できることが示されており、各所で使われるようになっている。
 練習:解析解の使用
練習:解析解の使用
上のPythonコードでは、スコア関数のトレーニング用データの作成に、実際に順方向の拡散をシミュレーションを行っている。 ところが、O-U過程の解析解(式(5))がわかっているので、トレーニングデータは正規乱数を使って生成することができる。そこで、
for i in range(N): x0 = x0s[i] x = fwd_diffuse(x0,t) # <==== この箇所 dlogp = - B *(x - x0*math.exp(-B*t))/(D*(1-math.exp(-2*B*t))) x_train.append(x) dlogp_train.append(dlogp)
の矢印の箇所を、正規乱数を使って書き直しなさい。
確率流を使った決定論的なサンプリング
位置と時間に依存する確率密度$p(x,t)$は、確率の保存から、連続の式 $$ \frac{\partial p(x,t)}{\partial t} + \frac{\partial}{\partial x} \left\{ v(x,t) \, p(x,t) \right\} = 0 \tag{6} $$ を満たす。 ここで、$v(x,t)$は$x$にある状態の「速度」に対応しており、多数の粒子で系が構成されている場合を想定すると、$x$にある粒子の移動速度 $\frac{dx}{dt}$に対応する。
ここで、O−U過程の逆過程のフォッカー・プランク方程式(式3) $$ \frac{\partial p(x,t)}{\partial \tau} + \frac{\partial}{\partial x} \left\{ \left(v(x,t) B x + R \frac{\partial \log p(x,\tau)}{\partial x} \right) \, p(x,\tau) \right\} = 0 $$ を $$ \frac{R}{2} \frac{\partial^2 p}{\partial x^2} = \frac{R}{2} \frac{\partial}{\partial x} \left\{ \frac{\partial \log p}{\partial x} p\right\} $$ を使って変形すると、式(6)の速度$v(x,t)$の箇所は $$ v(x,t) = B x + \frac{R}{2} \frac{\partial \log p(x,\tau)}{\partial x} $$ となる。 このことから、「粒子」を多数用意して、 $$ \frac{dx}{dt} = B x + \frac{R}{2} \frac{\partial \log p(x,\tau)}{\partial x} $$ に従って動かせば、確率分布の連続性を保ったまま、状態を遷移させることができる。 すなわち、確率過程の中から、保存則を保つような経路をひとつピックアップするわけである。
そこで、ランジュバン方程式を使って拡散の逆プロセスを計算するのではなく、$\frac{\partial \log p(x,\tau)}{\partial x}$のところはスコア関数で代用しつつ、 上記の決定論的なダイナミクス(確率フロー常微分方程式)を使って、サンプリングを行う方法が提案されている。
 練習:確率フローを使った生成
練習:確率フローを使った生成
前節の一次元拡散モデルのシミュレーションコードの後半部分を、確率フロー常微分方程式(の差分)を使った計算に変更して、動作を確認してみなさい。
(書きかけ)