傾向スコアマッチング
このページでは、傾向スコアマッチングについて考える(ここは書きかけ)。
二群の公正な比較
「・・は体によい(と言われている)。」
巷にはこのような言説が溢れているが、真偽のほどはどうかな、と感じつつも、もし健康に悪く無いのであれば、 「たまたま」自分にプラスの効果あればラッキー、と思いながら試してみたりするケースが多いのではないだろうか。
薬や食品に限らず、何らかの介入を行った結果、その効果の有無は公正に検証されなければならない。 ところが、それは原理的に困難である。 何故なら、理想的には同じ人に対してその介入をした場合としなかった場合を比較すべきであるが、それはそもそも不可能であるからだ。 (言うまでもなく、一旦介入すれば、その人にとっては「介入しなかった場合」を調べることは出来ないから。)
そこで次なる策として考えられるのは、実験対象を全くランダムに2つのグループに分け(それをA群とB群とする)、A群にのみ介入(例えばある医療行為)を行い、 その後の経過を観察してAとBを統計的に比較する方法である(いわゆるABテスト)。 ところが、こうした方法も事実上、実施が困難な場合が多い。 その介入が被験者の利益・不利益に影響する場合には、敢えて不利益な選択を実験の実施側が選択するのは倫理的な問題を孕むからである(そのため、そうした実験は倫理審査で許可されない)。
例えば、大量の飲酒が癌の発症に及ぼす影響を疫学的に調査しようとする場合、被験者をランダムに二分して、片方に強制的に飲酒させるような実験は(今日においては)不可能である。
他方で、企業が実施する広告の効果など、対象者の利害にあまり影響が無い場合は、この種の調査はよく行われているようである。 例えば、クッキーを使えば、ウェブブラウザを使っている個人が特定できる(「誰」かは分からなくても、同一人物かどうかは推測できる)。 そこで、利用者毎にランダムにウェブ広告の実施方法を変えて、その後の購買傾向を比較することができる。 この場合、対象となるグループをランダムに選択することで、グループ間のバイアスを実効的に無くすことが可能となる。
では、無作為化比較試験(randomised controlled trial, RCT)も不可能な場合に、介入の効果を公正に評価するにはどうしたら良いのだろうか。
例えば、飲酒が癌の発症に対する影響を調べている場合を想定してみよう。 一定以上飲酒しているグループを介入群、 飲酒していないグループを対照群として、 それぞれのグループから、同じような属性(年齢や性別、生活習慣や生活環境、等々)を持つペア同士を比べて、癌の発症率を比較ることができれば、グループ間のバイアスを減じることができそうだ。
ところが、全く同じ属性を持った人間は、同じ環境で育てられた一卵性双生児くらいしか見いだせないだろう。 そこで、個人が調査対象のグループの中で「どのあたり」に位置しているのかを表す指標(傾向スコア, propensity score)を与えて、その指標を使って、ペアとなる対象を決めることにする。 この傾向スコアは、以下のように、ロジスティック回帰によって評価する方法が一般的である。
飲酒量と、癌の発症以外の、個々人の属性を表現する説明変数(共変量(covariate)と呼ばれる)として、$i$番目の対象の年齢を $a_i$、肥満の程度 $b_i$、喫煙の有無 $c_i$が 調査されているとしよう(これは、あくまで架空の設定である)。 そして、飲酒量が多いグループは $x_i=1$、少ないグループは$x_i=0$として、データからロジスティック回帰を行う。 得られた回帰パラメータを$w_0, w_1, w_2, w_3$とすれば、「傾向」が$(a, b, c)$ であるような人が飲酒量の多いグループに属する確率は $$ P(X=1 | a,b,c) = \frac{1}{1 + e^{- (w_0 + w_1 a + w_2 b + w_3 c)} } $$ と見積もることができ、この条件付き確率を傾向スコア(propensity score)とする。 そして、このスコアが近い者同士は、(飲酒量について考える上では)近い性質を持っていると考えるのが自然であろう。 実用的には、この確率そのものではなく、指数関数の肩の部分(logit) $$ \textrm{logit}(a,b,c) = w_0 + w_1 a + w_2 b + w_3 c $$ を傾向スコアの違いの物差し(キャリパー)として用いる。
結果に影響するかもしれない、未知の、あるいは測定が困難な共変量が存在する可能性は残されているし、 変数の間に簡単な一次式的な(超平面的な)関係が成り立つことも一般には保証されないので、 上記はそれなりに大胆な仮定を置いていることになる。
傾向スコアのマッチング
次に、飲酒量が多いグループと少ないグループから、ロジスティック回帰から算出された傾向スコアが近い者同士を比較する。 それには、傾向スコアが近い者同士でペアを構成するのが分かりやすいが、 異なるサンプルに対して傾向スコアが完全に一致する状況は一般には少なく、グループ間で人数の偏りが生じたりもするので、ペアの作り方には任意性(曖昧さ)が残る。 そこで、いくつかの実際的なアルゴリズムが提案されている。
その中でも実装が簡単なのは、貪欲アルゴリズム(greedy algorithm)によって最近傍を選ぶ方法である。
1: 処置群の傾向スコアのリスト T と、対照群の傾向スコアのリスト C を用意する。 2: Tが空になるまで以下を繰り返す: 3: Tからランダムに要素を選ぶ。選んだ要素の番号をi、その傾向スコアを T[i] とする。 4: Cの要素の中から T[i] に最も値が近いものを探す。その傾向スコアを C[j] とする。 5: もし、T[i]とC[j]の差があらかじめ決めた値より小さければ 6: iとjをペアとして登録し、C[j]を削除する 7: T[i]を削除して、2:から繰り返す
Pythonの辞書のキーに人、値に傾向スコアを対応させ、貪欲アルゴリズムでマッチングを行うコードの例を以下に示す。
変数dlimitが近傍とみなすしきい値を与え、結果は、辞書の形でPに格納される。
サンプルをランダムに選ぶことから、実行の都度、結果として得られるペアは異なる。
# coding: utf-8
import random
import sys
T = {'a':0.32, 'b':0.67, 'c':0.39, 'd':0.97, 'e':0.12, 'f':0.75, 'g':0.51, 'h':0.57,
'i':0.49, 'j':0.43, 'k':0.68, 'l':0.47, 'm':0.80, 'n':0.73, 'o':0.56, 'p':0.23,
'q':0.39, 'r':0.60, 's':0.10, 't':0.35, 'u':0.93, 'v':0.55, 'w':0.45, 'x':0.34}
C = {'A':0.74, 'B':0.42, 'C':0.10, 'D':0.52, 'E':0.77, 'F':0.39, 'G':0.43, 'H':0.60,
'I':0.28, 'J':0.50, 'K':0.39, 'L':0.35, 'M':0.28, 'N':0.81, 'O':0.30, 'P':0.61,
'Q':0.32, 'R':0.21, 'S':0.06, 'T':0.85, 'U':0.71, 'V':0.46, 'W':0.68, 'X':0.26,
'Y':0.32, 'Z':0.37}
dlimit = 0.2
P = { }
while len(T)>0:
i = random.choice(list(T))
score0 = T[i]
dmin=sys.float_info.max
for key,val in C.items():
score1 = val
if abs(score0-score1) < dmin:
dmin = abs(score0-score1)
j = key
if dmin <= dlimit:
P[i] = j
del C[j]
del T[i]
print(P)
ここで述べた貪欲アルゴリズムは、部分的に最適解を求める手続きを繰り返すため、必ずしも全体的に最適なペアリングが行われる保証は無い。 そこで、ペア同士のスコアの距離の和を最小にするような方法(「最適アルゴリズム」)も考えられるが、 最悪のケースでは、全ての組み合わせを試すとサンプル数の階乗程度の手間を要する。
また、傾向スコアが近いもの同士で1対1のペアを構成するのではなく、 介入群と対照群のどちらのサンプルも十分な数だけ存在するような範囲で、傾向スコアをいくつかの区間に分け、 同じ区間内のサンプル同士を比較する方法も使われる。
このようにして、対象の属性についてバランスの取れた2群が得られたならば、 一定の信憑性のもとに、効果量等を用いた2群の比較が可能となる。
おもちゃモデルでのシミュレーション
では、素性が知れているデータを簡単なモデルで生成して、傾向スコアマッチングが有効に働くかどうか、そのデータを使って検証してみよう。
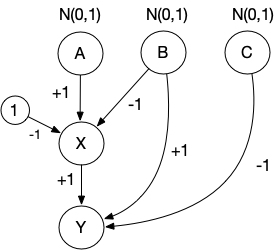
まず、3つの独立な確率変数 $$ \begin{eqnarray} A & \sim & \textrm{Normal}(0,1) \\ B & \sim & \textrm{Normal}(0,1) \\ C & \sim & \textrm{Normal}(0,1) \\ \end{eqnarray} $$ を考え、これらから、0と1の二値を取る確率変数$X$ (treatmentに対応)が $$ P(X=1) = \frac{1}{1+e^{-(a - b - 1)}} $$ で生成されると考える。 さらに、これらから$Y$ (outcomeに対応)が $$ Y = X + B - C $$ で誘導されるとしよう(下図)。 $X$と$Y$に着目すると、このモデルでは$B$が交絡因子となっている。
上記のルールに従って、Pythonでサンプルデータを出力するコードの例を以下に示す:
# coding: utf-8
import random
import numpy as np
import math
N = 500
A = np.random.normal(0,1,(N,))
B = np.random.normal(0,1,(N,))
C = np.random.normal(0,1,(N,))
X=[]
for a,b in zip(A,B):
px = 1/(1+math.exp(-(a - b - 1.0)))
x = np.random.choice((0,1),p=(1-px,px))
X.append(x)
X = np.array(X)
Y=[]
for b,c,x in zip(B,C,X):
y = x + b - c
Y.append(y)
Y = np.array(Y)
print("A,B,C,X,Y")
for a, b, c, x, y in zip(A, B, C, X, Y):
print("{0:.1f},{1:.1f},{2:.1f},{3},{4:.1f}".format(a,b,c,x,y))
このプログラムで出力したサンプルデータをファイル
sample-data-abcxy.csv
として用意した。
試みに、このデータについて、$X=0$(322件)と$X=1$(178件)の2群に対し、$Y$の平均の差について効果量(Hedgesのg)を計算してみると 約0.1であり、顕著な差は見いだせない。 それは、交絡因子$B$の効果が$X$と$Y$とでは逆になるようにモデルを設定しているので、$X$の$Y$への効果が「撹乱」されているため、と解釈できるだろう。 したがって、$B$が近いもの同士を比較することで、$X$の効果をより正当に評価できるはずである。
そこで、以下のコードを使って、このデータファイルを読み込み、傾向スコアマッチングを行い、マッチングされたペア同士の差を調べてみる:
# coding: utf-8
import numpy as np
import random
import math
import sys
import pandas as pd
from sklearn.linear_model import LogisticRegression
from scipy import stats
# CSVデータを読み込み
table = pd.read_csv("sample-data-abcxy.csv")
data = table.values
ndata = data.shape[0]
# 0:A
# 1:B
# 2:C
# 3:X 0 or 1
# 4:Y
# A,B,Cを説明変数、Xを目的変数としてロジスティック回帰
U = [ ]
X = [ ]
for row in data:
x0 = row[0] # A
x1 = row[1] # B
x2 = row[2] # C
x3 = row[3] # X
U.append([x0,x1,x2])
X.append(x3)
lr = LogisticRegression(max_iter=1000)
res = lr.fit(U,X)
print(lr.coef_[0])
print(lr.intercept_)
# 回帰パラメータを用いて傾向スコアを計算
T = { }
C = { }
E0 = [ ]
E1 = [ ]
for i,row in enumerate(data):
x0 = row[0] # A
x1 = row[1] # B
x2 = row[2] # C
x3 = row[3] # X
x4 = row[4] # Y
logit = lr.coef_[0][0]*x0 + lr.coef_[0][1]*x1 + lr.coef_[0][2]*x2 + lr.intercept_[0]
if x3==0:
C[i] = logit
E0.append(1/(1+math.exp(-logit)))
else:
T[i] = logit
E1.append(1/(1+math.exp(-logit)))
# print(C)
# print(T)
# 貪欲アルゴリズムでCとTのマッチング
dlimit = 0.05
P = { }
E2 = [ ]
E3 = [ ]
while len(T)>0:
i = random.choice(list(T))
logit0 = T[i]
dmin=sys.float_info.max
for key,val in C.items():
logit1 = val
if abs(logit0-logit1) < dmin:
dmin = abs(logit0-logit1)
lgtmem = logit1
j = key
if dmin <= dlimit:
P[i] = j
del C[j]
E2.append(1/(1+math.exp(-lgtmem)))
E3.append(1/(1+math.exp(-logit0)))
del T[i]
print(P)
# 対応する2群として差を検定
D = [ ]
for t, c in P.items():
d = data[t,4] - data[c,4]
D.append(d)
print(D)
n = len(D)
s1 = sum(D)/n
s2 = 0
for d in D:
s2 += (d - s1)**2
s2 = s2/(n-1)
tval = (s1 - 0)/math.sqrt(s2/n)
print("N=",n)
print("T=",tval)
pval = stats.t.cdf(x=-abs(tval),df=n-1)*2
print("Pval=",pval)
# 傾向スコアのヒストグラム表示
import matplotlib.pyplot as plt
fig = plt.figure()
ax0 = fig.add_subplot(1, 4, 1)
ax0.hist(E0)
ax0.set_title("X=0")
ax0.set_xlim(0.0,1.0)
ax1 = fig.add_subplot(1, 4, 2)
ax1.hist(E1)
ax1.set_title("X=1")
ax1.set_xlim(0.0,1.0)
ax2 = fig.add_subplot(1, 4, 3)
ax2.hist(E2)
ax2.set_title("X=0(MATCHED)")
ax2.set_xlim(0.0,1.0)
ax3 = fig.add_subplot(1, 4, 4)
ax3.hist(E3)
ax3.set_title("X=1(MATCHED)")
ax3.set_xlim(0.0,1.0)
plt.tight_layout()
plt.show()
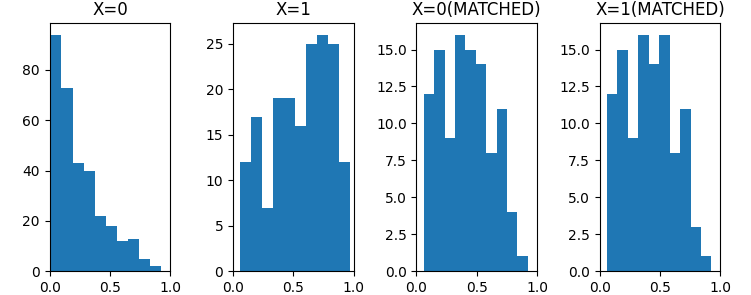
上のコードでは、サンプルのバランスを確認するため、マッチング前とマッチン後の傾向スコアのヒストグラムを最後に表示するようにしている。 以下はその例であるが、傾向スコアの分布をマッチングの前後で比較すると、マッチングを行うことで、分布が揃えられていることが判る。
対応する2群について『両者に差は無い』という帰無仮説を設定して、$Y$の差をt検定すると、 t統計量は5程度(マッチングによって多少変動する)、p値は$10^{-5}$以下となって、帰無仮説は棄却される。 すなわち、モデルで仮定したとおり、$X$が$Y$に影響している可能性が強く示唆される結果となる。
筆者は医学や医療について全くの素人であるため、以下に記す内容についての信ぴょう性については保証できかねます。 アルゴリズムやPythonコードの例として参照してください。
タバコの肺ガンへの影響
タバコが健康に悪影響を及ぼすのは疑いの無いところであろうが、実際には如何ほどの効果があるものだのだろうか。 Kaggleに、 検査を受けた患者の状況と、その結果、肺ガンが見つかったかどうかについての データ が掲載されていたので、それを使って考察してみよう (データの出典などは明記されていない点には注意)。
データセット
(survey lung cancer.csv)には
コラム名 データの内容 --------------------- ----------------------------- GENDER male=M fimale=F AGE SMOKING no=1 yes=2 YELLOW_FINGERS no=1 yes=2 ANXIETY no=1 yes=2 PEER_PRESSURE no=1 yes=2 CHRONIC DISEASE no=1 yes=2 FATIGUE no=1 yes=2 ALLERGY no=1 yes=2 WHEEZING no=1 yes=2 ALCOHOL CONSUMING no=1 yes=2 COUGHING no=1 yes=2 SHORTNESS OF BREATH no=1 yes=2 SWALLOWING DIFFICULTY no=1 yes=2 CHEST PAIN no=1 yes=2 LUNG_CANCER YES NO
について284名分の診察データがテーブル形式で与えられている。
† データセットをダウンロードするにはKaggleにサインインする必要があります(無料)。
喫煙と肺ガンの有無の関連性に着目して、データを調べてみると
喫煙者 174名 (うち肺ガン発見 155名) 割合 0.89
非喫煙者 135名 (うち肺ガン発見 115名) 割合 0.85
であり、割合には殆ど違いが無いようにも見える。
ここで、傾向スコアを用いて、同じような属性を持つ喫煙者と非喫煙者をマッチングし、対応のある2群として、肺ガンの発症割合を比較してみよう。 以下は、前節のコードを元に、データに合わせて調整してみた例である:
# coding: utf-8
import numpy as np
import random
import math
import sys
import pandas as pd
from sklearn.linear_model import LogisticRegression
from scipy import stats
# CSVデータを読み込み:データを1 or 2に変換
table = pd.read_csv("survey lung cancer.csv")
table['GENDER'] = table['GENDER'].apply(lambda x: 1 if x=='M' else 2)
table['LUNG_CANCER'] = table['LUNG_CANCER'].apply(lambda x: 1 if x=='NO' else 2)
data = table.values
ndata = data.shape[0]
# "Lung Cancer"
# from https://www.kaggle.com/datasets/mysarahmadbhat/lung-cancer
# 0:GENDER M/F
# 1:AGE
# 2:SMOKING 1/2
# 3:YELLOW_FINGERS 1/2
# 4:ANXIETY 1/2
# 5:PEER_PRESSURE 1/2
# 6:CHRONIC DISEASE 1/2
# 7:FATIGUE 1/2
# 8:ALLERGY 1/2
# 9:WHEEZING 1/2
# 10:ALCOHOL CONSUMING 1/2
# 11:COUGHING 1/2
# 12:SHORTNESS OF BREATH 1/2
# 13:SWALLOWING DIFFICULTY 1/2
# 14:CHEST PAIN 1/2
# 15:LUNG_CANCER YES/NO
# 喫煙の有無を目的変数としてロジスティック回帰
U = [ ]
X = [ ]
for row in data:
x0 = row[0]
x1 = row[1]
x2 = row[2]
x3 = row[3]
x4 = row[4]
x5 = row[5]
x6 = row[6]
x7 = row[7]
x8 = row[8]
x9 = row[9]
x10 = row[10]
x11 = row[11]
x12 = row[12]
x13 = row[13]
x14 = row[14]
U.append([x0,x1,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14])
X.append(x2-1.0)
lr = LogisticRegression(max_iter=1000)
res = lr.fit(U,X)
print(lr.coef_[0])
print(lr.intercept_)
# 回帰パラメータを用いて傾向スコアを計算
T = { }
C = { }
E0 = [ ]
E1 = [ ]
for i,row in enumerate(data):
x0 = row[0]
x1 = row[1]
x2 = row[2]
x3 = row[3]
x4 = row[4]
x5 = row[5]
x6 = row[6]
x7 = row[7]
x8 = row[8]
x9 = row[9]
x10 = row[10]
x11 = row[11]
x12 = row[12]
x13 = row[13]
x14 = row[14]
logit = lr.coef_[0][0]*x0 + lr.coef_[0][1]*x1
+ lr.coef_[0][2]*x3 + lr.coef_[0][3]*x4 + lr.coef_[0][4]*x5
+ lr.coef_[0][5]*x6 + lr.coef_[0][6]*x7 + lr.coef_[0][7]*x8
+ lr.coef_[0][8]*x9 + lr.coef_[0][9]*x10 + lr.coef_[0][10]*x11
+ lr.coef_[0][11]*x12 + lr.coef_[0][12]*x13 + lr.coef_[0][13]*x14
+ lr.intercept_[0]
if x2==1:
C[i] = logit
E0.append(1/(1+math.exp(-logit)))
else:
T[i] = logit
E1.append(1/(1+math.exp(-logit)))
# print(C)
# print(T)
# 貪欲アルゴリズムでCとTのマッチング
dlimit = 0.05
P = { }
E2 = [ ]
E3 = [ ]
while len(T)>0:
i = random.choice(list(T))
logit0 = T[i]
dmin=sys.float_info.max
for key,val in C.items():
logit1 = val
if abs(logit0-logit1) < dmin:
dmin = abs(logit0-logit1)
lgtmem = logit1
j = key
if dmin <= dlimit:
P[i] = j
del C[j]
E2.append(1/(1+math.exp(-lgtmem)))
E3.append(1/(1+math.exp(-logit0)))
del T[i]
print(P)
# 対応する2群として差を検定
D = [ ]
for t, c in P.items():
d = data[t,15] - data[c,15]
D.append(d)
print(D)
n = len(D)
s1 = sum(D)/n
s2 = 0
for d in D:
s2 += (d - s1)**2
s2 = s2/(n-1)
tval = (s1 - 0)/math.sqrt(s2/n)
print("N=",n)
print("T=",tval)
pval = 1.0 - stats.t.cdf(x=tval,df=n-1)
print("Pval=",pval)
# 傾向スコアのヒストグラム表示
import matplotlib.pyplot as plt
fig = plt.figure()
ax0 = fig.add_subplot(1, 4, 1)
ax0.hist(E0)
ax0.set_title("NONSMOKERS")
ax0.set_xlim(0.1,0.4)
ax1 = fig.add_subplot(1, 4, 2)
ax1.hist(E1)
ax1.set_title("SMOKERS")
ax1.set_xlim(0.1,0.4)
ax2 = fig.add_subplot(1, 4, 3)
ax2.hist(E2)
ax2.set_title("NONSMOKERS(MATCHED)")
ax2.set_xlim(0.1,0.4)
ax3 = fig.add_subplot(1, 4, 4)
ax3.hist(E3)
ax3.set_title("SMOKERS(MATCHED)")
ax3.set_xlim(0.1,0.4)
plt.tight_layout()
plt.show()
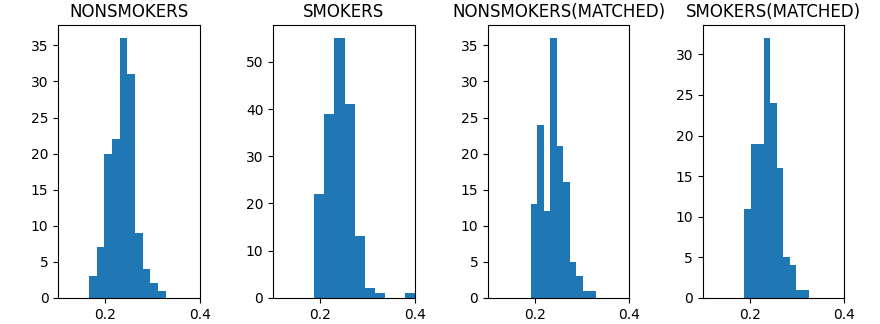
上記のコードでは、喫煙者と非喫煙者の2群を対応づけ、 帰無仮説『2つのグループには平均に差は無い』を設定し、対立仮説としては『喫煙者は発症率が高い』を採用して片側のt検定を行っている。 サンプル数は 135で、計算の結果得られる t統計量は約 0.5〜1.3 程度、 p値は約 0.3〜0.1 程度となり(いずれもマッチングの結果によって変わる) 喫煙の肺ガン発症への影響を強く支持する結果とはならなかった。
傾向スコアの分布を比較すると、マッチング後に2群の分布がより近づいている様子が確認できると共に、傾向スコア自体の違いは僅かで、 2群それぞれの傾向が共変量に大きくは依存していないことが伺える。
 練習:フィッシャーの正確検定
練習:フィッシャーの正確検定
喫煙の有無と肺ガンの有無についての分割表について、喫煙の有無に対する死亡率の違いをフィッシャーの正確検定をしてみなさい。
| 肺ガン無し | 肺ガン発症 | |
|---|---|---|
| 喫煙 | 174 | 155 |
| 非喫煙 | 135 | 115 |
 練習:研究デザイン
練習:研究デザイン
上記のデータでは、受診した患者の多くが一般の喫煙比率よりも多く喫煙をしているように見受けられ、 また、喫煙しない群も、何らかの異常を感じて受診しているはずである。 このように肺ガンと喫煙の関連性を調べる上で、そもそもサンプルが大きく偏っていると思われる。
では、信憑性のある結果を得るためには、どのように研究をデザインしたら良いか、考えてみなさい。
(書きかけ)