Pythonプログラミング（ステップ７・多変数の最尤推定と最小二乗法）

このページでは、多次元の場合の最尤推定（最小二乗法）について考える。

多次元データの線形モデル

ある量 $Y_1$ が、複数の量$\{X_1, X_2, \cdots, X_m \}$ に線形に依存して変化するものの、揺らぎ（ノイズ）$\xi_1$を伴う現象を考える。 以下では、$Y_1$, $X_j$ の平均は0とする。 平均が0でないような場合でも、あらかじめ各量の平均値を計算し、それを差し引くような「前処理」を行っておけば、以下の議論がそのまま適用できる。 この状況を具体的な数式で表すと $$ Y_1 = \sum_{i=1}^{m} a_i X_i + \xi_1 \tag{1} $$ となる。ここで、$a_i$は各変数の影響度の大きさ（重み）を表すパラメータである。 $\xi_1$は、観測と度にランダムに変化するとし、簡単のため、その平均は0とする。 これは、最小二乗法のページの内容を高次限に拡張しただけである。

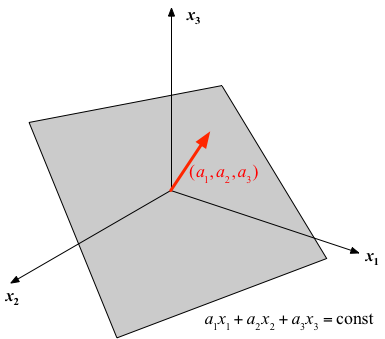
もし$\xi_1=0$かつ$Y_1$を定数とおくと、(1)式は、$(X_1, X_2, \cdots, X_m)$　空間の平面を表す方程式となっている。 言い換えれば、揺らぎ$\xi_1$を除けば、(1)式は、$m$次元空間の平面と、$Y_1$との対応関係を与える式になっている。

$X_i$についての揺らぎや誤差は無く、$\xi_1$がガウス型の確率分布（平均0、分散$\sigma^2$）に従うとすると $j$番目の観測によって、データの組 $Y_1=y_{1,j}$、$X_i = x_{i,j}$が得られる確率は $$ P(y_{1,j}, \{x_{i,j}\}) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{\left(y_{1,j} - \sum_i a_i x_{i,j} \right)^2}{2 \sigma^2} \right) $$ となる。$N$個の独立なデータについて確率は $$ P(\{y_{1,j}, \{x_{i,j}\}\}) = \frac{1}{(2\pi)^{N/2} \sigma^N} \exp\left(-\frac{\sum_{j=1}^N \left(y_{1,j} - \sum_i a_i x_{i,j} \right)^2}{2 \sigma^2} \right) $$ となるから、尤度を最大にするためには、2変数の場合と全く同様に、 $$ R = \sum_{j=1}^{N} \left( y_{1,j} - \sum_{i=1}^m a_i x_{i,j} \right)^2 \tag{2} $$ を最小化すればよい。

$R$が極小になる条件として、パラメータで偏微分して0とおくと $$ \frac{\partial R}{\partial a_k} = - 2 \sum_{j=1}^N x_{k,j} \left( y_{1,j} - \sum_{i=1}^m a_i x_{i,j} \right) = 0 \tag{3} $$ ここで、パラメータと変量をベクトルと行列を使って表記する： $$ \boldsymbol{a} = \left( \begin{array}{c} a_1 \\ a_2 \\ \vdots\\ a_m \end{array} \right) $$ $$ \boldsymbol{y} = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots\\ y_N \end{array} \right) $$ $$ X= \left( \begin{array}{cccc} x_{1,1} & x_{1,2} & \cdots & x_{1,N} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,N} \\ \vdots & & & \vdots \\ x_{m,1} & x_{m,2} & \cdots & x_{m,N} \end{array} \right) $$

これらの表記を使って、$R$が極値となる条件(3)を書き直すと、 $$ - 2 X \boldsymbol{y} + 2 X X^\top \boldsymbol{a} = 0 $$ すなわち $$ X X^\top \boldsymbol{a} = X \boldsymbol{y} $$ が得られる。 ここで、左辺の $X X^\top$ は正方行列で、データの分散共分散行列の$N$倍である。 また、右辺の $X \boldsymbol{y}$ は、$X$と$Y$の共分散（の$N$倍）である。 $X X^\top$が正則であれば、その逆行列を左から作用させて、パラメータ$\boldsymbol{a}$が $$ \boldsymbol{a} = \left( X X^\top \right)^{-1} X \boldsymbol{y} \tag{4} $$ として求められる。 このように、分散共分散行列の逆行列が計算できれば、モデルのパラメータを決定できる。

ここで、 $$ \left( X^\top X \right)^{-1} X^\top $$ は行列$X$のMoore-Penroseの疑似逆行列（一般逆行列）と呼ばれる。

データの中に相関の強い項目があったとしよう。極端な場合として $k$ 番目と $\ell$ 番目の項目に比例関係 $x_{k,i} \propto x_{\ell,i}$ が成り立っていると 分散共分散行列$X^\top X$の$k$列（行）と$\ell$列（行）に互いに独立にならず、その結果、逆行列が計算できない（行列式が0となる）。 また、比例関係に近い場合でも、計算結果が不安定となってしまうことが知られている。 このように、データの間の強い相関（比例関係）を多重共線性(colinearllity)と呼び、回帰係数の計算や解釈にあたり、注意が必要である。

$R$を極小化するための別のアプローチとして、$\epsilon$を十分小さな数として $$ a_k \leftarrow a_k - \epsilon \frac{\partial R}{\partial a_k} = a_k + 2 \epsilon \sum_{j=1}^N \left( y_{1,j} - \sum_{i=1}^m a_i x_{i,j} \right) \, x_{k,j} \tag{5} $$ を全ての$k$について繰り返すことで、$R$の勾配方向に「下る」方法も考えられる。

$Y$が$\ell$個の変数の組の場合でも、$Y_j$ に付随する揺らぎを $\xi_j$ として、$\xi_j$と$\xi_k$ $(j \neq k)$が互いに無相関であれば、全く同様に考えることができて、 $$ Y = \left( \begin{array}{cccc} y_{1,1} & y_{1,2} & \cdots & y_{1,N} \\ y_{2,1} & y_{2,2} & \cdots & y_{2,N} \\ \vdots & & & \vdots \\ y_{\ell,1} & y_{\ell,2} & \cdots & y_{\ell,N} \end{array} \right) $$ $$ A = \left( \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,\ell} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,\ell} \\ \vdots & & & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,\ell} \end{array} \right) $$ とおけば $$ A = \left( X X^\top \right)^{-1} X Y^\top \tag{6} $$ となる。形式的には (Xの共分散)^-1 (X,Yの共分散) という形にまとめられる。

自己回帰モデル

離散時間$t=0,1,2,\cdots$に対して得られる時系列データを $x(t)$ とするとき、(1)式の各データを、 $Y_1 \to x(t), \; X_1 \to x(t-1), \; X_2 \to x(t-2), \cdots$ と対応付けたモデル $$ x(t) = \sum_{j=1}^{m} a_j x(t-j) + \xi(t) \tag{7} $$ を考えてみよう。ここで、異なる時刻のノイズ$\xi(t), \; \xi(t')$は互いに無相関であるとする。 この式は $t-1, \cdots, t-m$の過去のデータから、1ステップ先（$t$）を予測する格好になっている。

ここで、長さ$N+1$の時系列 $x(0), x(1), \cdots, x(N)$が観測されたとき、観測量から構成されるベクトル、 $$ \boldsymbol{x} = \left( x(m), x(m+1), x(m+2), \cdots, x(m+N) \right) $$ および行列 $$ X= \left( \begin{array}{ccccc} x(m-1) & x(m) & x(m+1) & \cdots & x(m+N-1) \\ x(m-2) & x(m-1) & x(m) &\cdots & x(m+N-2) \\ x(m-3) & x(m-2) & x(m-1) &\cdots & x(m+N-3) \\ \vdots & & & & \vdots \\ x(0) & x(1) & x(2) &\cdots & x(N) \end{array} \right) $$ を定義すると、式(4)により、パラメータの最尤推定値は $$ \boldsymbol{a} = \left( X X^\top \right)^{-1} X \boldsymbol{x}^\top \tag{8} $$ で得られることになる。

パーセプトロン

上記のとおり、最小二乗法は、ガウス分布する揺らぎと密接に関係している。 ところが、揺らぎ（確率的挙動）はガウス的ばかりとは限らない。 そこで、ここでは、最小二乗法には還元されない例として、ロジスティック回帰（あるいは単層パーセプトロン）を取り上げておく。

$n$次元のベクトル $(x_1, x_2, \cdots, x_m)$ を与えると、 0 または 1 を$y$に出力する「機械」のモデルとして、 $$ y = F \left( \sum_{j=1}^m a_j x_j \right) \tag{9} $$ を考えよう。 ここで、$F(s)$は、$s$を0または1を確率的に出力する「変換器」で、1を出力する確率がシグモイド関数 $$ P(s) = \frac{1}{1 + \exp(- \beta s)} \tag{10} $$ で与えられるとする。

そして、出力 $y$ が、与えられたデータ・セット $\{ (y_i, \, x_{1,i}, \, x_{2,i}, \cdots, \, x_{m,i}) \}$ に対して、できるだけ近い出力と なるように、パラメータ $\{a_j\}$ を調整したい。

これは、ある種の神経の動作を単純化したモデルともなっている。$x_j$は$j$番目のシナプスに対する入力信号、$a_j$はその入力に対する敏感姓（シナプス荷重）、そして複数の入力信号の「荷重付き合算」によって出力$y$が決まる、という考え方である。

その文脈では、データ $(y_i, \, x_{1,i}, \, x_{2,i}, \cdots, \, x_{m,i})$ は教師信号と呼ばれ、教師信号にできるだけ「近い」振る舞い方をするようにパラメータ $\{a_j\}$ を決めるのが「学習」という解釈になる。そして、ここで述べているモデルは、パーセプトロン(perceptron)と呼ばれる神経回路のモデルの一種に他ならない。

パラメータを与えたとき、$i$番目のデータセットに対して1を出力する確率を $f_i$ と表すことにすると、 $$ f_i = \frac{1}{1 + \exp \left( -\beta \sum_{j=1}^m a_j x_{j,i} \right) } $$ となる。逆に0を出力する確率は、$f_i$を使って、 $$ 1-f_i $$ となる。 すると、出力が$y_i$（ここで$y_i$は0または1）となる確率は $$ {f_i}^{y_i} (1-f_i)^{1-y_i} $$ と書くことができる（0乗は常に1であることに注意）。

$N$組のデータに対して、この機械が正しく動作する確率（尤度）は、変換器の確率的な挙動が互いに独立とすると、データ毎の確率の積 $$ \prod_{i=1}^N {f_i}^{y_i} (1-f_i)^{1-y_i} $$ となる。その対数を取ると、対数尤度が $$ \begin{eqnarray} L & = & \sum_{i=1}^N \left[ y_i \log(f_i) + (1-y_i) \log(1-f_i) \right] \\ & = & - \sum_{i=1}^N y_i \log\left[1+ \exp \left( -\beta \sum_{j=1}^m a_j x_{j,i} \right) \right] - \sum_{i=1}^N (1-y_i) \log\left[1+ \exp \left(\beta \sum_{j=1}^m a_j x_{j,i} \right) \right] \end{eqnarray} $$ となる。

対数尤度$L$を最大化するパラメータの組 $\{a_j\}$ を直接的に解くことは難しいので、 $L$がだんだんと大きくなるように、少しずつ $\{a_j\}$ を変化させる作戦を採用する。 パラメータ$L$の$a_k$方向の勾配は $$ \frac{\partial L}{\partial a_k} = \beta \sum_{i=1}^N y_i x_{k,i} (1-f_i) - \beta \sum_{i=1}^N (1-y_i) x_{k,i} f_i = \beta \sum_{i=1}^N y_i x_{k,i} - \beta \sum_{i=1}^N x_{k,i} f_i $$ となる。そこで、十分に「小さな」数を $\epsilon$ として、 $$ a_k \leftarrow a_k + \epsilon \sum_{i=1}^N (y_i - f_i) \, x_{k,i} \tag{11} $$ によってパラメータを更新する操作を反復すれば、少しずつ対数尤度を上げることができる($\beta$は定数なので$\epsilon \beta$を$\epsilon$と置き直した) 。 これは、$N$個のデータ全体に対して更新を行うアルゴリズム（バッチ処理）になっているが、実用的には、データ毎に $$ a_k \leftarrow a_k + \epsilon \; (y_i - f_i) \, x_{k,i} $$ のように、$k$番目の荷重を調整してもうまく動作する。

上式は非常にわかりやすい形になっている。$y_i - f_i$は、教師信号（望ましい出力）と、あるデータ入力$\{x_j\}$に対してその「神経」が実際に1を出力する確率との「食い違い」を表す。 そして、そのときの入力$x_k$と「食い違い」との積に応じて $a_k$ を調整せよ、というのが式の意味するところである。

式(11)の学習則は、線形モデルの逐次的パラメータ修正の式(5)と同じ形をしている。パーセプトロンの出力 $y$ の期待値は連続量になり、それが $f_i$ に他ならないので、それが線形モデルの$Y_1$と対応していることになる。 データ点のばらつきに比べて $1/\beta$が大きい（$\beta$が小さい）場合、２つのモデルに本質的な違いは無い、とも言える。

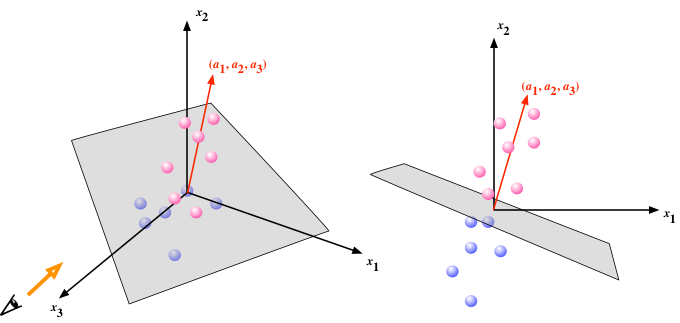
パーセプトロンは、$(a_1, a_2, \cdots, a_m)$を法線とするような超平面を境として、データ点を「あちら」と「こちら」に分類する（出力を0か1かに振り分ける）動作をする。下図の青丸を「あちら（出力0）」、赤丸を「こちら（出力1）」と見立て、動作の様子を考えてみるとよい。

以上は、超平面が原点を含むケースを考えたが、法線方向に平面を平行移動することも許し、 $$ y = F \left( \sum_{j=1}^m a_j x_j - b \right) $$ とするのがパーセプトロンのモデルとしては一般的である（$b$をバイアスと呼ぶ）。 こちらのモデルのパラメータの求め方（学習則）は、バイアス無しで、ただし常時1の入力をひとつ追加したモデル $$ y = F \left( \sum_{j=1}^{m} a_j x_j + a_{m+1} \cdot 1 \right) $$ として考えればよい。