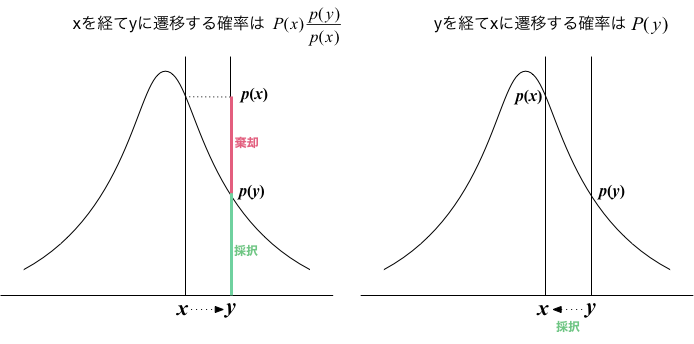メトロポリス法
このページでは、複雑な確率分布をサンプリングする手法のひとつ、メトリポリス法について紹介する。
状態遷移と棄却法を組み合わせた乱数生成
正規分布に従う乱数列を得るアルゴリズムは色々と知られているし、Pythonに標準装備されているrandomモジュールを使えば
random.gauss(平均, 標準偏差) で簡単に得ることができるが、ここでは、それらを全く知らないものと仮定して、
正規乱数を生成する方法を考えてみよう。まず、目的とする確率密度を
$$
p(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}
$$
とする。
いま状態が $x$ であったとして、その次にどのような値 $y$ を出力すべきかを決める判定基準を考える。
その際、とりあえず、乱数(例えば [-1,1]の範囲の一様乱数。左右対称な分布を持つ乱数ならば何でもよい)$\xi$を使って、 $$ y = x + \xi $$ として、新しい$y$の候補を生成する。
ここで、$p(y) \le p(x)$の場合を考えてみよう(下図)。 そして、候補$y$を採択し、状態を$x$から$y$に遷移させる確率を $$ \alpha = \frac{p(y)}{p(x)} $$ のように選択する($1-\alpha$の確率で候補を棄却する)。
他方で、これと全く反対の状況、すなわち $y$に状態があって、$x$が候補として選ばれた場合 (このとき $p(y) \le p(x)$ )は、無条件に(確率1で) 状態を $y$ から $x$ に遷移させるルールを採用する。
状態が$x$にある確率を(大文字で)$P(x)$と書くことにすると、$x$という状態を経て$y$が採択される確率は $$ P(x) \frac{p(y)}{p(x)} $$ であり、反対に、$y$という状態を経て$x$が採択される確率は $$ P(y) \cdot 1 $$ である。
確率の「流れ」の量が$x \to y$と$y \to x$で釣り合って入れば、 全体としては、あたかも流れていないように見えるはずである。 一般に、流れの量は、モノの量と速さの積になるが、$x \to y$の場合 $P(x)$がモノの量、$p(y|x)$が速さに対応する。
確率過程(マルコフ連鎖)の理論が教えるところによれば、$x$を経て$y$に遷移する率と、$y$を経て$x$に遷移する率がちょうどバランスするとき(詳細釣り合い)、 更新を繰り返すうちに「自然に」定常的な分布(不変分布)が得られる。 そして、上記の更新ルールでは、不変分布が目標とする分布にちょうど一致する($P(x)=p(x)$)ときに、詳細釣り合い $$ P(x) \frac{p(y)}{p(x)} = P(y) $$ が実現されるよう、うまい具合に工夫されている。 つまり、発生する$x$の系列の分布関数は目的分布($p(x)$)になっているはずである。
上記の議論は、最初に$p(y) \le p(x)$と仮定したが、$p(y) \gt p(x)$の場合でも、$x$と$y$の役割を入れ替えれて考えれば全く同じことである。
以上をまとめると、確率密度$p(x)$に従う乱数列を生成するアルゴリズム(メトロポリス法)は次のようになる:
- $x$の初期値を設定する
- 「左右」対称な乱数 $\xi$ を使って、候補 $y = x + \xi$ を発生させる
- $p(y) \le p(x)$ ならば、$\alpha = \frac{p(y)}{p(x)}$ の確率で $y$ を採択する。(採択しない場合は状態は$x$のまま)。
- $p(y) \gt p(x)$ ならば、$y$ を採択する。
- 更新した$y$を$x$と置き直す。
- 「ときどき」$x$を出力する。
- 2から6のステップを繰り返す。
ここで、「ときどき」は、状態についての記憶(相関)が消えるくらいのステップ数、を意味する。
メトロポリス法では、棄却の判定条件($\alpha$の計算)に確率分布の比率のみを用いるので、そこで用いる分布関数は規格化されていなくても構わない。
メトロポリス法で正規分布に従う乱数列を発生させ、その分布を表示するPythonコードの例を以下に示す:
# coding: utf-8
import random
import math
import matplotlib.pyplot as plt
def p(x):
return 1/math.sqrt(2*math.pi)*math.exp(-x**2/2)
x = 0
sdata=[ ]
cnt=0
for _ in range(1000000):
y = x + random.uniform(-1,1)
alpha = min(1, p(y)/p(x))
r = random.uniform(0,1)
if r > alpha:
y = x
x = y
cnt += 1
if cnt%10==0:
sdata.append(x)
xdata=[]
ydata=[]
x=-5.0
while x<5.0:
xdata.append(x)
ydata.append(p(x))
x += 0.01
plt.title("NORMAL DISTRIBUTION")
plt.plot(xdata,ydata,color=(0.0,0.0,0.7))
plt.hist(sdata, bins=100, density=True, color=(1.0,0,0.0))
plt.xlabel('x')
plt.ylabel('P(x)')
plt.legend()
plt.grid(True)
plt.show()
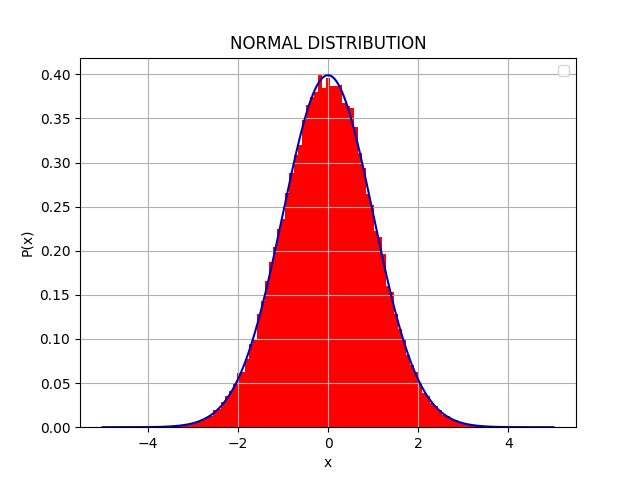
実行結果。赤棒がシミュレーションの結果得られたヒストグラム、青線が目的とした分布。
 練習:二次元のガウス分布
練習:二次元のガウス分布
メトロポリス法を使って、確率密度が $$ p(x,y) \propto \exp\left( -x^2 + x y - 2 y^2 \right) $$ となるような乱数列$X,Y$を生成するPythonコードを書いてみなさい。
2次元のイジング模型
二次元の正方格子上に、小さな磁石(スピン)が並んでいて、隣(上下左右)と影響を及ぼし合っている。 磁石は「上向き」、または「下向き」に対応して+1と-1の2種類の状態のどちらかを取り、 隣同士が同じ向きのときは $-J$、互い違いの向きのときは $+J$ のエネルギーを持つと仮定する($J$が正であれば、向きが揃ったほうがエネルギーが低くなる)。 このとき、磁石の位置を $(i,j)$ で指定す、その場所の状態を $s_{i,j}$ で表現することにすると、系全体のエネルギーは $$ E = - J \sum_{i,j} s_{i,j} \, \left( s_{i-1,j} + s_{i+1,j} + s_{i,j-1} + s_{i,j+1} \right) \tag{1} $$ となる(外場のない正方格子のイジング模型)。
スピン配列を $\{\cdots,s_{i,j},\cdots\}$ で表すことにすると、統計力学によれば、そのような配列が実現する確率は、 $$ P(\{\cdots,s_{i,j},\cdots\}) = \frac{1}{Z} \exp\left( - \frac{E(\{\cdots,s_{i,j},\cdots\})}{k_B T} \right) $$ となる(ここで、$Z$は規格化定数(分配関数)、$T$は温度、$k_B$はボルツマン定数)。
スピンの揃いやすさ$J$が熱揺らぎの程度$k_B T$よりも大きければスピンが全体して揃いやすくなり、反対に、$J$が相対的に小さいと、 熱揺らぎによってスピンの向きはランダムになる。 では、$\frac{J}{k_B T}$ の大きさの程度によって全体的な振る舞いがどのように変わるのだろうか。 興味深いことには、ある$\frac{J}{k_B T}$の値を境に、全体的な振る舞いが「突如として」変わってしまうことが分かっている(相転移と呼ぶ)。 その様子を、ここではメトロポリス法を使って再現してみよう†。
イジング模型の計算は、こちらのページで説明したように、ギブスサンプリングを使ったアルゴリズムでも可能である。 イジング模型の場合は各スピンの取り得る状態数が2つのみなのでギブスサンプリングが容易に実装できるが、状態が連続値を取るような問題を扱う場合は、メトロポリス法が適している。
エネルギーの式(1)を見ると、+1と-1について全く対称な形をしている。にもかかわらず、$\frac{J}{k_B T}$がある値よりも大きい(温度が低い)と、スピンが全体として「自発的に」+1または-1に揃うようになる。このように、各要素が全体のことは気にせず、ローカルルールで「勝手に」振る舞うにもかかわらず、体系の巨視的な振る舞いにおおきな違いや特徴が現れることを協力現象(cooperative phenomenon)とか自己組織化現象(self-organizing phenomenon)等と呼んで、研究されている。二次元のイジング模型はこうした協力現象の存在が理論的に厳密なかたちで示された最初の例である。
ひとつのスピン $s_{i,j}$ に注目し、そのスピンの状態を反転させて$s_{i,j}'$にしたとする。 すなわち、$s_{i,j}=1$ならば$s_{i,j}'=-1$、 $s_{i,j}=-1$ならば$s_{i,j}'=1$、である。 反転を行う前と後の確率の比率を考えると、 $$ \alpha = \frac{P(\{\cdots,s_{i,j}',\cdots\})}{P(\{\cdots,s_{i,j},\cdots\})} = \exp\left[\frac{J}{k_B T} (s_{i,j}'-s_{i,j})(s_{i-1,j} + s_{i+1,j} + s_{i,j-1} + s_{i,j+1}) \right] $$ となる。近傍(上下左右)のみと相互作用していることと、指数関数の性質から、$(i,j)$に隣接するスピンの状態しか$\alpha$には反映されない。 また、規格化定数 $Z$ も分子と分母でキャンセルする。 ここで、$s_{i,j}'=-s_{i,j}$なのだから、 $$ \alpha = \exp\left[\frac{-2 J}{k_B T} s_{i,j} (s_{i-1,j} + s_{i+1,j} + s_{i,j-1} + s_{i,j+1}) \right] $$ と書いても構わない。
メトロポリス法によるイジング模型のシミュレーション
以上を踏まえると、二次元イジング模型の物理的な確率分布(カノニカル分布)をシミュレーションで再現するためには、以下のようにすればよい:
- $J/(k_B T)$を決め、$s_{i,j}$に初期値を設定する(-1または+1)
- $i,j$を一様かつランダムに選択する
- $\alpha$を計算する
- $[0,1]$の一様乱数 $r$ を生成する
- $r \lt \min(1,\alpha)$ なら、$s_{i,j}$を反転させる(そうでなければ、そのままにしておく)
- (必要に応じて、磁化などの量を計算する)
- 2から6までを反復する
このアルゴリズムをPythonコードに翻訳した例を以下に示す。 状態を可視化するため pygletライブラリ(バージョン1.5.27以前)を使用しているので、必要に応じて追加インストールする必要がある。
右のコードでは変数Jが$\frac{J}{k_B T}$に対応する。
Nは系全体の大きさ(差し渡し)で、全体で$N^2$のスピンとなる。
SCALEは、スピン1つあたりのマス目の大きさ。
# coding: utf-8
import pyglet
from pyglet.gl import *
import random
import math
import numpy as np
# グローバル変数
J=0.4
N=100
SCALE=4
s=np.zeros([N,N])
counter=0
def alpha(i,j):
return math.exp(-2*J*s[i,j]*(s[(i-1)%N,j]+s[(i+1)%N,j]+s[i,(j-1)%N]+s[i,(j+1)%N]))
# 初期化
def init_state():
global s
for i in range(N):
for j in range(N):
s[i,j] = random.choice([-1,+1])
# 状態更新
def update_state(n):
global s,counter
for _ in range(n):
i = random.randrange(0,N,1)
j = random.randrange(0,N,1)
a = min(1,alpha(i,j))
r = random.uniform(0,1)
if r < a:
s[i,j] = -s[i,j]
counter += 1
def next_frame(dt):
return
def redraw():
update_state(1000)
for i in range(N):
for j in range(N):
if s[i,j]>0:
glColor3d(0.8,0.3,0.1)
else:
glColor3d(0.2,0.6,0.7)
glBegin(GL_POLYGON)
glVertex2d((i+0)*SCALE,(j+0)*SCALE)
glVertex2d((i+1)*SCALE,(j+0)*SCALE)
glVertex2d((i+1)*SCALE,(j+1)*SCALE)
glVertex2d((i+0)*SCALE,(j+1)*SCALE)
glEnd()
m = np.sum(s) / (N*N)
t = counter/(N*N)
label = pyglet.text.Label('t='+str(t)+' m='+str(m),
font_name='Helvetica', color=(255,255,255,255),
font_size=12, x=10, y=10)
label.draw()
init_state()
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
win.set_caption('2-d Ising Model')
@win.event
def on_draw():
glClear(GL_COLOR_BUFFER_BIT)
glClearColor(0,0,0,1)
redraw()
pyglet.clock.schedule_interval(next_frame, 1/10.0)
pyglet.app.run()
Pythonコードを実行している様子(YouTube)。 赤錆色が+1、浅葱色が-1。
Pyglet version 2用のコード
Pyglet 2以上をお使いの方はこちらのコードをお試しください。
import pyglet
from pyglet.gl import *
import random
import math
import numpy as np
# グローバル変数
J=0.4
N=100
SCALE=4
s=np.zeros([N,N])
counter=0
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
win.set_caption('2-d Ising Model')
batch = pyglet.graphics.Batch()
def alpha(i,j):
return math.exp(-2*J*s[i,j]*(s[(i-1)%N,j]+s[(i+1)%N,j]+s[i,(j-1)%N]+s[i,(j+1)%N]))
# 初期化
rects = np.empty(shape=(N,N),dtype='object')
def init_state():
global s
for i in range(N):
for j in range(N):
s[i,j] = random.choice([-1,+1])
rect = pyglet.shapes.Rectangle(x=i*SCALE, y=j*SCALE, width=SCALE, height=SCALE, batch=batch)
if s[i,j]>0:
rect.color = (230,50,20)
else:
rect.color = (30,170,200)
rects[i,j] = rect
@win.event
def on_draw():
glClear(GL_COLOR_BUFFER_BIT)
glClearColor(0,0,0,1)
for i in range(N):
for j in range(N):
rect = rects[i,j]
if s[i,j]>0:
rect.color = (230,50,20)
else:
rect.color = (30,170,200)
batch.draw()
m = np.sum(s) / (N*N)
t = counter/(N*N)
label = pyglet.text.Label('t='+str(t)+' m='+str(m),
font_name='Helvetica', color=(255,255,255,255),
font_size=12, x=10, y=10)
label.draw()
# 状態更新
def update_state(n):
global s,counter
for _ in range(n):
i = random.randrange(0,N,1)
j = random.randrange(0,N,1)
a = min(1,alpha(i,j))
r = random.uniform(0,1)
if r < a:
s[i,j] = -s[i,j]
counter += 1
def update(dt):
update_state(1000)
init_state()
pyglet.clock.schedule_interval(update,1/10)
pyglet.app.run()
 練習:二次元イジング模型
練習:二次元イジング模型
上のコード例を元にして、全体的にスピンの向きが揃う・揃わないの境界となるような$\frac{J}{k_B T}$を見積もってみなさい。