ギブスサンプリング

このページでは、ギブスサンプリングは「何をやっているのか」、「どのような計算に使えるのか」についてあれこれ考えてみる。

状態とその間の遷移

家族（父親と母親、そしてその子供）の血液の遺伝型を考える。母親の遺伝型を $x_M$、父親のそれを $x_F$、その子供を$x_C$ と表すことにしよう。$x_M$, $x_F$, $x_C$ は、それぞれ aa, ao, ab, .... といった遺伝型を取り得る。 すると、この家族の遺伝型は $(x_M, x_F, x_C)$の組によって指定されることになる。

たった親子３名であっても、遺伝子型の組み合わせはかなりの数になる。不可能な組合わせ(aaとaaの親とooの子、等）も含めて単純計算すると $6^3 = 216$ 通りであり、さらに大きな家系図では、組み合わせの数が指数的に増大することは明らかであろう。

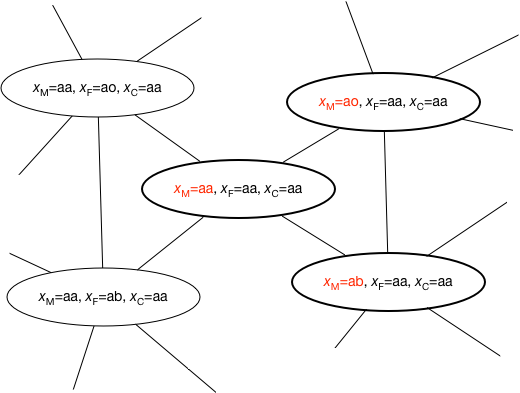
それぞれの状態をノードとし、一人分の遺伝子型だけが異なるもの同士を結んで図にすると、その一部は以下のようになる。 図では、可能な遷移のみを線で示している。

ここで、このネットワーク上を行ったり来たり移動している「旅人」を想像しよう。 旅人が状態 $(x_M=\textrm{aa}, x_F=\textrm{aa}, x_C=\textrm{aa})$ に居たとして、 変数のうちの一つ、例えば、$x_M$ に注目する。 そして、$x_M$が取り得る aa、ao、abという３つの可能性を（ベイズの公式に従って） $$ P( \textrm{M:}xy, \textrm{F:aa} | \textrm{C:aa} ) = \frac{P( \textrm{C:aa} | \textrm{M:}xy, \textrm{F:aa}) P(\textrm{M:}xy)} {\sum_{x,y} P( \textrm{C:aa} | \textrm{M:}xy, \textrm{F:aa}) P(\textrm{M:}xy)} $$ の確率で選び、その確率に応じて上図で太線の丸で示した状態のどれかに場所を移動する。

このときもし、状態変数として$x_C$を選んだとすると、移れる先が無い（aaとaaの親からはaaの子供しか生まれない）から、状態遷移も起こらない。

こうした操作を繰り返すと、たった三人の親子の家系図に対してもネットワークには沢山のノードがあるから、旅人は確率的な揺らぎを伴って、それらのノードを経巡ることになる。

内部状態（この場合は$x_M, x_F, x_C$の組）によって別の状態への遷移確率が決められるような確率的な連鎖反応をマルコフ連鎖、 乱数を使ったアルゴリズムをモンテカルロ法と呼ぶことから、このような計算手法は、マルコフ連鎖モンテカルロ（Markov chain Monte Carlo; MCMC）法と総称されている。

状態から状態へ確率的に（ランダムに）何度も移動する場合、長期的な可能性として考えられるのは以下の３通りである（道に迷った場合の可能性、といってもよいかもしれない）。

1. 行き止まりにあたって、それ以上進めない
2. 同じ経路をぐるぐる廻り続ける
3. 全体（またはその一部の領域）をランダムに何度も再訪する

状態を $\boldsymbol{x} = (x_1,x_2, \cdots, x_i, \cdots)$ で表すとすると、 ギブスサンプリングでは、$i$を均等に選んだ上で、$i$番目の状態変数以外が与えられたときに、 $$ p(x_i| \cdots,x_{i-1},x_{i+1},\cdots) $$ を求め、「次のとなり」を決める。このとき、状態 $(x_1,x_2, \cdots, x_i, \cdots)$ が次に選ばれる確率は $$ p(x_1,x_2, \cdots, x_i, \cdots) \leftarrow p(x_i| \cdots,x_{i-1},x_{i+1},\cdots) p(\cdots,x_{i-1},x_{i+1},\cdots) $$ であるから、長期的に3のような定常的な状況が達成されている場合、「旅人」が状態を訪れる頻度が「知りたかった」確率分布 $p(\boldsymbol{x})$ となっているはずである。

血液の遺伝子型の例では、旅人のノード $(x_M, x_F, x_C)$ への訪問回数の頻度が $p(x_M, x_F, x_C)$ を与えることになる。

多変数の確率分布に従う乱数の生成

前節で述べた遺伝子型の分布は、結合確率 $p(x_M, x_F, x_C)$ が複雑で導出が難しい場合に、 それを局所的な確率遷移に「小分け」することで、シミュレーションが可能となるような例であった。

複雑な結合確率をギブスサンプリングによってシミュレーションする別の例として、正値を取り、結合確率が $$ p(x,y) = \frac{1}{N} e^{-x-xy-y} $$ となるような確率変数 $X, \, Y$ $(\ge 0)$について考えてみよう。ただし、$N$は規格化定数で $$ N = \int_0^{\infty} \int_0^{\infty} e^{-x-xy-y} dx dy $$ である。

ここで、目的とする$p(x,y)$を、 $$ p(x,y) = p(x|y) p(y) = p(y|x) p(x) $$ のように分解して考えてみると、例えば、$p(x|y)$ は $$ p(x|y) = \frac{1}{N'} e^{-(1+y)x} $$ （$N'$は規格化定数）となって、$x$のみに着目すれば、単純な指数分布に帰着できる。

うまいことに、指数分布 $$ p(z;a) = a e^{-az} $$ （$a \gt 0$）に従うような乱数は、一様乱数 $U$ ($0 \lt U \lt 1$)を使って $$ Z = \frac{-\log(U)}{a} $$ によって生成できる（逆関数法のページを参照）。

以上を組み合わせると、目的とする確率分布 $p(x,y)$ に従う乱数は、ギブスサンプリングの手法によって

1. 適当な初期値の組 $(x,y)$ を設定する
2. $x \leftarrow \frac{-1}{1+y}\log(U)$ で $x$を更新する
3. $y \leftarrow \frac{-1}{1+x}\log(U)$ で $y$を更新する
4. 2と3を多数回繰り返しながら、$(x,y)$を「ときどき」出力する。

の手順で生成することができる

ここで、「ときどき」と書いたのは、$(x,y)$についての記憶（相関）が失われるくらいのステップ毎に、という意味である。

この例では、$X, Y$は連続値を取るので、状態数（ノードの数）は非加算無限個あるが、ギブスサンプリングでは 「その時点での」状態だけ記憶しておけば良いので、必要となる計算ステップ数は別として、コンピュータでの処理が可能となる。

　練習：シミュレーション

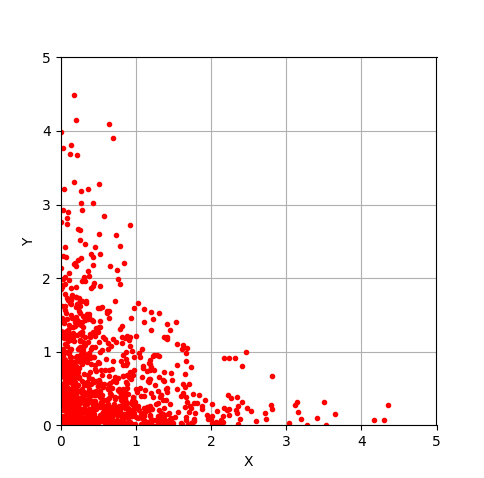
上記のアルゴリズムに従って、実際に $(x,y)$を出力し、その分布の様子を図のようにプロットするPythonコードを書いてみなさい。

１次元のイジング模型

図のように、一次元的に、+1と-1の状態を持つ小さな磁石（スピン）が並んでいて、隣同士と影響を及ぼし合っているとしよう。 ここでは、隣の向きが揃っている（+1と+1、または-1と-1）と $-J$ のエネルギーが、向きが逆の場合(+1と-1または-1と+1）は $+J$ のエネルギーが生じる 場合について考えよう。 また、系全体に外部磁場 $H$ が加わっているとする。 $i$番目のスピンの状態を変数 $s_i$ で表すことにすると、全体としてのエネルギー $E$ は $$ E(s_0, s_1, \cdots, s_i, \cdots) = -J \sum_i s_i s_{i+1} - H \sum_i s_i $$ となる。 これは、一次元イジング模型と呼ばれている。

統計力学の教えるところによれば、温度 $T$ の状況で（この系が温度$T$の熱浴と接しているとき）、状態 $(s_0, s_1, \cdots, s_i, \cdots)$ が生じる結合確率は $$ p(s_0, s_1, \cdots, s_i, \cdots) = \frac{1}{Z} \exp\left( - \frac{E(s_0, s_1, \cdots, s_i, \cdots)}{k_B T} \right) \tag{1} $$ で与えられる。 ここで、規格化定数 $Z$ は、全ての状態についての和 $$ Z = \sum_{s_0, s_1, \cdots, s_i, \cdots} \exp\left( - \frac{E(s_0, s_1, \cdots, s_i, \cdots)}{k_B T} \right) \tag{2} $$ として与えられ、統計力学では特に重要な役割を演ずることから、分配関数と命名されている。 また、$k_B$は温度をエネルギーの次元に換算するための定数で、ボルツマン定数と呼ばれる。

全体として磁石がどれくらい揃っているか（全体の磁化）は、スピンの総和 $$ M(s_0, s_1, \cdots, s_i, \cdots) = \sum_i s_i \tag{3} $$ で与えられるので、その平均は $$ \sum_{s_0, s_1, \cdots, s_i, \cdots} M(s_0, s_1, \cdots, s_i, \cdots) p(s_0, s_1, \cdots, s_i, \cdots) \tag{4} $$ で計算できる。

物理的に興味のある量（磁化のような平均量）を計算するには、このように、スピンの状態についての結合確率を使った総和（積分）を行う必要があるが、 その計算は一部の簡単な例を除けば、なかなか手ごわい。

そこで、ギブスサンプリングの考え方に従って、$i$番目以外の場所の状態が与えられているとき、 $i$番目のスピンが-1あるいは+1を取る確率を計算してみよう。

すると、$s_i=-1$と$s_i=1$について、条件付き確率 $$ P(s_i=\pm 1| \cdots,s_{i-1},s_{i+1},\cdots) = \frac{P(\cdots,s_{i-1},s_{i+1},\cdots | s_i=\pm 1) P(s_i=\pm 1)} {P(\cdots,s_{i-1},s_{i+1},\cdots | s_i=-1) P(s_i=-1) + P(\cdots,s_{i-1},s_{i+1},\cdots | s_i=+1) P(s_i=+1)} \tag{5} $$ を評価すればよい（複合同順）。

ここで、 $$ \begin{eqnarray} P(\cdots,s_{i-1},s_{i+1},\cdots | s_i=\pm 1) P(s_i=\pm 1) \\ = P(\cdots,s_{i-1},s_i=\pm 1, s_{i+1},\cdots) \\ = \frac{1}{Z} \exp\left( - \frac{E(\cdots,s_{i-1},s_i=\pm 1, s_{i+1},\cdots)}{k_B T} \right) \end{eqnarray} $$ である。$i$番目のスピンはその両隣としか影響を及ぼしあっていない点に注意しながらエネルギーのところを具体的に書くと、 $$ E(\cdots,s_{i-1},s_i=-1, s_{i+1},\cdots) = -J \sum_{j=0}^{i-1} s_{j-1} s_{j} - H \sum_{j=0}^{i-1} s_j + ( J s_{i-1} + J s_{i+1} + H) - J \sum_{j=i+1} s_{j} s_{j+1} - H \sum_{j=i+1} s_j $$ および $$ E(\cdots,s_{i-1},s_i=+1, s_{i+1},\cdots) = -J \sum_{j=0}^{i-1} s_{j-1} s_{j} - H \sum_{j=0}^{i-1} s_j - (J s_{i-1} + J s_{i+1} + H) - J \sum_{j=i+1} s_{j} s_{j+1} - H \sum_{j=i+1} s_j $$ となる。

つまり、結合確率は途中で「分断」することができて、 $$ P(\cdots,s_{i-1},s_i=\pm 1, s_{i+1},\cdots) = \frac{1}{Z} \; P'(\cdots,s_{i-1}) P'(s_{i-1},s_i=\pm 1, s_{i+1}) P'(s_{i+1}, \cdots) $$ のように書くことができる。ここで $P'$は規格化定数を除いた部分を表す。 すると、条件付確率の式(5)の分子と分母は、$i$の前後の箇所を除けば、全てキャンセルしてしまうことがわかる。

ここで、ボルツマン因子の中の符号にも注意しながら計算すると $$ P'(s_{i-1},s_i, s_{i+1}) = \exp\left(\frac{J s_i (s_{i-1} + s_{i+1}) + H s_i}{k_B T} \right) $$ となるから、結局、 $$ P(s_i| \cdots,s_{i-1},s_{i+1},\cdots) = \frac{\exp\left(\frac{J s_i (s_{i-1} + s_{i+1}) + H s_i}{k_B T} \right)} {\exp\left( + \frac{J (s_{i-1} + s_{i+1}) + H}{k_B T} \right) + \exp\left( - \frac{J (s_{i-1} + s_{i+1}) + H}{k_B T} \right)} \tag{6} $$ が得られる。 同じことであるが、$i$番目のサイト選んだら、 $$ P(s_i=1| \cdots,s_{i-1},s_{i+1},\cdots) = \frac{1} {1 + \exp\left(- 2 \frac{J (s_{i-1} + s_{i+1}) + H}{k_B T} \right)} \tag{6'} $$ の確率で+1に（さもなくば-1に）セットすればよい。

以上をまとめると、一次元イジング模型の磁化の平均を計算するアルゴリズムは以下のとおりとなる：

1. 温度と、相互作用パラメータおよび外部磁場の比率（$J/(k_B T)$、$H/(k_B T)$）を設定する
2. $\{s_i\}$の初期条件を与える
3. ランダムかつ一様に$i$を選ぶ
4. 式(6)に従った確率で$i$の状態を変更する
5. 式(3)で磁化を求める（複数回サンプルを取って平均化する）
6. 値が落ち着くまで3から5までを繰り返す

　練習：1次元イジング模型

上記のアルゴリズムをPythonコードで実現しなさい。

　ヒント

import random

# -1と1のどちらかをランダムに選択する
s = random.choice([-1,1])

# 0からN-1まで1間隔でひとつを選択
i = random.randrange(0,N,1)