モンテカルロ法による積分
このページでは、乱数を使った「計算」の例として、モンテカルロ法による数値積分を考える。
超球の体積の計算
誰でも知っているとおり、半径1の円の面積は$\pi$, 半径1の球の体積は $\frac{4\pi}{3}$ である。 これをさらに一般化して、 $d$次元の半径1の球の体積は、 $$ V_d = \frac{\pi^{d/2}}{\Gamma\left(\frac{d}{2}+1\right)} $$ で与えられる。 ここで$\Gamma()$はガンマ関数である。 例えば、$d=1$の場合は、$V_1=2$であり、次元の増加とともに、$V_d$は一旦増加するが、$d=6$以上では減少に転じる。
もしこの公式を知らなかったとしたら、$d$次元球の体積をどのように見積もったら良いだろうか。
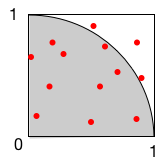
例えば、(二次元中の)半径1の円を考えてみよう。 そして、その面積を$S$とする。 $x$に0から1の範囲の一様乱数、$y$も同様とすると、点$(x,y)$は面積1の正方形の中に一様に分布するはずである。 そして、そのうちで、角度$\pi/4$の扇形 に入っているものの割合は、正方形と扇形の面積の比率、すなわち$S/4$となるだろう。 そうすると、$N$個の点を生成し、そのうち扇型に入っているものをカウント数した結果が$m$とすれば、 $$ \frac{m}{N} \approx \frac{S}{4} $$ すなわち、 $$ S \approx \frac{4m}{N} $$ と求まる。
ここでの発想のポイントは、ひとつには、面積が既知の図形(正方形)を基準にカウントすること、加えて、乱数の分布の一様性にある。
全く同様の発想で、$d$次元の球の体積を求めることができるはずだ。 辺の長さが1の$d$次元の立方体を考えると、その体積は1である。 その中に占める、$d$次元球の$1/2^d$の区画の割合から、超球の体積を推定するコードの例を以下に示す:
# coding: utf-8
import numpy as np
import math
d = 3
N=100000
cnt=0
for _ in range(N):
x = np.random.rand(d)
if np.linalg.norm(x) < 1:
cnt += 1
v = cnt/N * 2**d
print('v=',v)
このコードの中で、NumPyのnp.random.rand(d)関数は、0から1の範囲の一様乱数をd個生成し、そのリストを返す。
また、np.linalg.norm(x)は、リストxで与えられるベクトルの長さ(L2ノルム)を与える関数である。
 練習:球の体積
練習:球の体積
実際に上のコードを動作させ、数学的な(厳密な)結果と比較してみなさい。
 解説: 結果のゆらぎ
解説: 結果のゆらぎ
超球の体積を$V$とすれば、ランダムに生成された点が超球の内部に位置する確率は$p=V$である。 $N$回のサンプリングを行った場合、点が超球の内部にある回数は二項分布で与えられるので、その平均は、$N p$、分散は$N p (1-p)$である。 すると、体積の推定値のゆらぎは $$ \sqrt{\frac{p(1-p)}{N}} $$ となる。ここで、ゆらぎ(誤差)の$N$依存性は$d$には依存しない。
高次元での積分を、各次元ごとに$m$個のデータ点を使って計算しようとすると、データ点の総数は$N \sim m^d$程度で増大することになる。 例えば、台形法を使った場合の誤差は$\delta \sim 1/m^2$程度となるので、 $$ \delta \sim 1/m^2 \sim N^{-2/d} $$ であり、次元数$d$が大きくなると、同じ程度の計算精度を担保するに必要となる$N$は膨大となる。 言い換えると、高次元の問題になればなるほど、データ点数の観点からは、次元に関係なく$1/\sqrt{N}$程度で誤差(ゆらぎ)を減らすことができるモンテカルロ法が有利となってくる。
重点サンプリング
積分 $$ I = \int f(x) dx $$ の計算をモンテカルロ法で行う別の方法を考えてみよう。
ある素性の良い確率分布(提案分布)$q(x)$を用いて、 $$ \int f(x) dx = \int \frac{f(x)}{q(x)} q(x) dx $$ のように置き直すと、この積分は $q(x)$ についての $w(x) = \frac{f(x)}{q(x)}$ の平均を求める計算に帰着される。 よって、$q(x)$ の生成確率で乱数 $X_k$ を発生させることによって$w(X_k)$をサンプルすれば、 中心極限定理から $$ I \approx \frac{1}{N} \sum_{k=1}^N w(X_k) $$ によって積分の近似値を得ることができる。 この方法は、$q(x)$による確率的な荷重によってサンプリングを行うことから、重点サンプリング(importance sampling)と呼ばれている。 いわば、提案分布を「ものさし」にして積分を評価するわけである。
では、上記の線に沿って $d$ 次元の超球の体積を求めてみよう。
まず、半径1の球を表すために、原点からの距離$r$に依存した分布 $$ f(r) = \left\{ \begin{array}{cc} 1 & (r \lt 1) \\ 0 & otherwise \end{array} \right. $$ と考えると、この体積積分が超球の体積となる。
他方で、提案分布としてガウス分布 $$ q(r) = \frac{1}{\pi^{d/2}} e^{-r^2} $$ を考えてみる(平均0、分散$1/2$)。
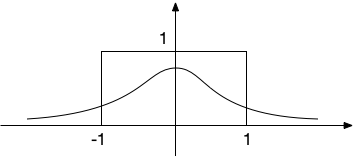
そして、$q(r)$の確率密度を持つような$d$次元の正規乱数$(x_1,x_2,\cdots,x_d)$を発生させ、 $r = \sqrt{{x_1}^2 + {x_2}^2 + \cdots + {x_d}^2} \lt 1$ならば $ w = 1/q(r) $ の、$1 \le r$ならば $w=0$ の重み付けを行って、点をサンプルすることにしよう。 このとき、サンプル数総数を$N$とし、$w_k$を$k$番目の重みとすれば、$f(r)$の積分、すなわち半径1の超球の体積 $V_d$ は $$ V_d \approx \frac{\sum_k w_k}{N} $$ で求められる。
# coding: utf-8
import numpy as np
import math
def normal(r,d):
return math.exp(-r**2) / math.sqrt(math.pi**d)
d = 10
N=100000
wt=0.0
for _ in range(N):
x = np.random.normal(loc=0, scale=1/math.sqrt(2), size=d)
r = np.linalg.norm(x)
if r < 1:
wt += 1/normal(r,d)
v = wt / N
v0 = math.pi**(d/2)/math.gamma(d/2+1)
print('v=',v,v0)
 解説: 高次元でのサンプリングの難しさ
解説: 高次元でのサンプリングの難しさ
上記のサンプル方法でどの程度効率的に積分が評価できるか考察してみよう。
簡単のため1次元の場合をまず考えて、$q(x)=\frac{1}{\sqrt{2\pi s^2}} \exp\left(-x^2/(2 s^2)\right)$ と置いてみる。 そして、サンプリングの効率(誤差)の指標として、$w(x)$ の分散を見積もることにする。
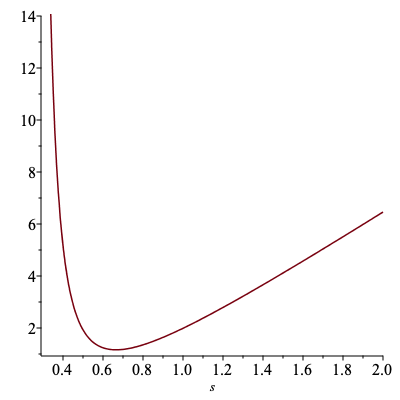
$w(x)$の平均(すなわち1次元球の体積)は、 $$ \bar{W} = \int_{-1}^{+1} \frac{1}{q(x)} q(x) dx = 2 $$ である。 他方で、$w(x)$の二乗平均は $$ \bar{W^2} = \int_{-1}^{+1} \left(\frac{1}{q(x)}\right)^2 q(x) dx = \sqrt{2 \pi } s^2 \int_{-1}^{+1} \exp\left(\frac{x^2}{2 s^2}\right) dx $$ となる。 これから、標準偏差$s$の関数として$w(x)$の分散 $$ \bar{W^2} - \bar{W}^2 $$ を数値計算してプロットすると、以下のようになる。 この値が小さいほど、より「的確」なサンプル値が得られるため、少ないサンプル回数でも良好な推定値が得られると期待できる。 プロットからは、$s$には最適値があり、それを外れると分散が急激に増大することがわかる。 そして、最適な$s$とは、提案分布が、$f(x)$になるべく近いかたちになるような値、と解釈できる。
こちらのプロットにはMapleを使用した。
$d$次元の場合にも全く同様の議論が可能であって、 $\bar{W}$ は$d$次元球の体積 $V_d$, すなわち $$ \bar{W} = V_d $$ $w(x)$の二乗平均は、被積分関数が方向に依存しないことから、動径方向のみの積分を考えれば十分で、 $$ \bar{W^2} = \left( 2 \pi s^2 \right)^{d/2} d V_d \int_{0}^{1} \exp\left(\frac{r^2}{2 s^2}\right) r^{d-1} dr $$ となる。 これらを用いて、$w(x)$の相対的なゆらぎの指標 $$ \frac{\bar{W^2}- \bar{W}^2}{\bar{W}^2} $$ を$d=8$の場合について計算し、プロットした例を以下に示す。
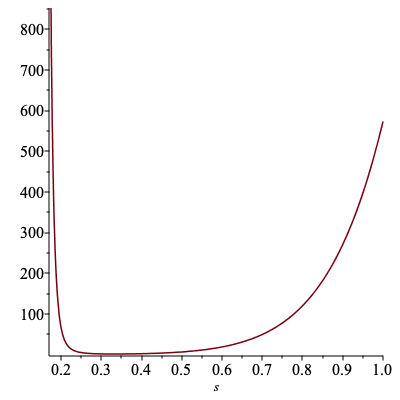
この様子からは、提案分布$q(x)$の選択の仕方によって、効率(計算誤差)は大きく左右されるだろうと予想される。 さらに、この傾向は次元$d$の増大と共に一層顕著となる。
 練習:サンプリング効率の比較
練習:サンプリング効率の比較
超球の体積を求める際、次元$d$が大きくなると、サンプル点が球の内側に入って「採択」される割合が急激に減少するため、著しく計算の効率と精度が低下してしまうことが知られている。
重点サンプリングで体積を求めるコードの例では、 提案分布$q(r)$として分散が1/2の正規分布を用いたが、その分散を変えられるようにし、計算の効率や精度が分散の大小によってどのように変わるか実験してみなさい。