感染症のデータ分析

このページでは、確率モデルを使って、感染間隔の分布や、感染症の感染が確認された人数の推移から新規発症者数を推定する方法などを考える。

発症間隔（serial interval）の分布の推定

ある人が感染した日を起点に、その人が新たな感染を生じさせるまでの間隔 $\tau$ (日数)の分布を考えてみよう（この間隔は serial inverval と呼ばれている）。 COVID-19についてのこちらの論文†では

3, 2, 4, 2, 2, 1, 4, 2, 10, 4, 3, 4, 4, 3, 3, 9, 9, 3, 4, 3, 9, 4, 5, 9, 7, 7, 3, 7

という28の時間間隔の例を用いた解析が行われている。 ここでは、簡単のため、それぞれのデータの重みは等しいと考え、これらの間隔がどのような分布形に従っているのかを推定してみよう。

上記の論文を参考に、その分布がWeibull分布 $$ f(\tau) = \frac{\alpha \tau^{\alpha-1} \exp\left(-\left(\frac{\tau}{\beta}\right)^\alpha \right)}{\beta^\alpha} $$ に従うとしてみる。内部モデルとして、パラメータ（いずれも正値）は対数正規分布に従う： $$ \begin{eqnarray} \alpha \sim \textrm{Lognormal} \\ \beta \sim \textrm{Lognormal} \end{eqnarray} $$ とし、観測モデルとして $$ \tau \sim \textrm{Weibull}(\alpha,\beta) $$ とおいて、PyMC3を使って分布関数のパラメータ$\alpha, \, \beta$を推定するコードの例を以下に示す。

# coding: utf-8

import math
import random
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt

intervals=[3,2,4,2,2,1,4,2,10,4,3,4,4,3,3,9,9,3,4,3,9,4,5,9,7,7,3,7]

with pm.Model() as model_weibull:
    alpha = pm.Lognormal('alpha')
    beta = pm.Lognormal('beta')
    tau = pm.Weibull('tau', alpha=alpha, beta=beta, observed=intervals)
    trace_w = pm.sample(chains=1, tune=2000, draws=1000)

a_m = np.mean(trace_w['alpha'])
a_s = np.std(trace_w['alpha'])
b_m = np.mean(trace_w['beta'])
b_s = np.std(trace_w['beta'])
print('alpha=',a_m,'+/-',a_s)
print('beta=',b_m,'+/-',b_s)

def weibull(x,alpha,beta):
    return (alpha/beta) * (x/beta)**(alpha-1) * np.exp(-(x/beta)**alpha)

x = np.linspace(0,20,100)
y = weibull(x,a_m,b_m)

plt.plot(x, y, color=(0.0,0.0,1.0), linewidth=1.0)
plt.xlabel('TAU (DAYS)')
plt.ylabel('F')
plt.grid(True)
plt.show()

　練習： モデルの比較

Weibull分布以外の連続分布（対数正規分布やガンマ分布等）について、同様の推定を行ってみなさい。 さらに、PyMC3のマニュアルを参考に、モデルの「良さ」を比較してみなさい。

　ヒント

発症から確認までの遅延

次に、新型コロナウイルスの感染拡大の様子を想定しながら、報道発表などで知られる「その日の新規感染者数」と、 実際に発症した日とのずれについて考察してみよう。

$t$ 日目で新たに確認された感染者数を $y(t)$ とする。 もちろん、これらの人は、それ以前に発症して、医療機関を受診し、検査の結果、罹患が確認されるわけである。 COVID-19の場合、その期間は数日から２週間程度に及ぶと言われているようである。 こうした時間遅れを発症から確認までの期間$\tau$の分布 $f(\tau)$ で表し、$t$日目に発症した人数を $x(t)$ とすれば $$ y(t) = \int_{0}^{\infty} f(\tau) \, x(t-\tau) \, d\tau $$ と表現することができるだろう。ここで、時間遅れの分布関数は規格化されている $$ \int_{0}^{\infty} f(\tau) \, d\tau = 1 $$ とする（$x(t)$と$y(t)$で、人数の総計は等しい）。

実際のデータは離散間隔（日毎）で集計される場合が多いので、 $$ y_t = \sum_{k=0}^{M} f_k \, x_{t-k} $$ のように扱うことになる。

ここで、沢山のサンプルから、遅延の分布型はあらかじめわかっているとしよう。 特にそうしたエビデンスがあるわけではないが、以下ではポアソン分布を仮定することにする： $$ f_k = \frac{\lambda^k e^{-\lambda}}{k!} $$ （平均時間遅れ $\lambda$ (日)、分散も $\lambda$ (日$^2$)。検査の結果が出るまでが長引けば、それだけ、いろいろな要因でばらつきも増すと考えるのは自然に思える）。

感染確認日からの感染日の確率的な推定

次に、$\{ y_0, y_1, \cdots, y_N\}$ がデータとして与えられたとき、$\{x_n\}$ を推定するという逆問題を解く方法について考えよう。

ナイーブには、連立方程式 $$ \begin{eqnarray} \begin{pmatrix} y_{0} \\ \vdots \\ y_{N-2} \\ y_{N-1} \\ y_{N} \\ \end{pmatrix} = \begin{pmatrix} f_{M-N+1}& \cdots & 0 & 0 & 0 \\ \vdots & & \vdots & \vdots &\vdots \\ f_{M-2} & \cdots & f_0 & 0 & 0 \\ f_{M-1} & \cdots & f_1 & f_0 & 0 \\ f_{M} & \cdots & f_2 & f_1 & f_0 \end{pmatrix} \; \begin{pmatrix} x_{0} \\ \vdots \\ x_{M-3} \\ x_{M-2} \\ x_{M-1} \\ x_{M} \\ \end{pmatrix} \end{eqnarray} $$ を $\{ x_n\}$ を未知数にして解けば良さそうな気もするが、$x_n$について何も仮定を置いていないので、結果として（大きな）負数が得られるなど、計算の目的に照らすと、あまりうまくいかないことが分かる（実際に試してみよ）。

X = (np.linalg.pinv(A)).dot(Y.T)

確率モデルによって考える

そこで、新規感染者の時系列 $\{x_n\}$ を生成する確率モデルを仮定し、そこから時間遅れを伴って生じている系列を我々が観測している、という立場で考えてみよう。

内部モデル

内部モデルとして、$n$日目の新規感染者数が $$ x_n = e^{z_0} \, e^{dz_0} \cdots e^{dz_{n-1}} = e^{z0 + dz_0 + dz_1 + \cdots + dz_{n-1}} $$ のように、拡大率 $e^{dz_n}$ の乗算的な過程で生じているとしよう。 このように考えることで、$x_n$は自動的に正値となる。 そして、拡大率の対数 $dz_n$ は正規分布していると仮定する： $$ dz_n \sim N(0,0.1^2) $$ また、その出発値 $z_0$ は $$ z_0 \sim N(0,1) $$ とおく。

観測モデル

この $\{ x_n \}$から、$n$日目に感染が確認された人数の平均が $$ \mu_n = \sum_{k=0}^{M} f_k \, x_{n-k} $$ と決まり、観測される人数はポアソン分布 $$ y_n \sim \textrm{Poisson}(\mu_n) $$ に従う、とモデル化する。

2020年1月25日から5月9日にかけての、東京都のCOVID-19の感染者数の時系列を例に、 PyMC3でこのモデルを記述してみた例を以下に示す。 オンセットから確認までの平均日数は14日とした（lambd=14）。

# coding: utf-8

import math
import random
import numpy as np
import pymc3 as pm
import theano.tensor as tt
from theano.compile.ops import as_op

# 2020/1/25〜5/9の東京都の陽性者数（累計）
y_cum =[
2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4,6,14,19,19,22,25,25,28,29,29,
32,32,35,36,36,37,39,39,40,44,52,58,64,64,64,67,73,75,77,87,90,90,102,
111,118,129,136,138,154,171,212,259,299,362,430,443,521,587,684,773,889,
1032,1115,1194,1338,1516,1703,1900,2066,2157,2316,2442,2590,2791,2972,3079,
3181,3304,3436,3570,3731,3834,3906,3945,4057,4104,4150,4315,4473,4564,4651,
4709,4747,4770,4809,4845
]

y_cum = np.array(y_cum)
y = np.diff(y_cum)
N = len(y)

M=63
kernel = np.zeros((M,))
lambd=14
tot = 0
for k in range(M):
    fk = lambd**k / math.factorial(k)
    tot += fk
    kernel[k] = fk
kernel = kernel/tot
kernel = np.roll(kernel, M//2)
    
@as_op(itypes=[tt.dvector],otypes=[tt.dvector])
def convolve(x):
    return np.convolve(x,kernel,mode='same')

model = pm.Model()
with model:
    z_0 = pm.Normal('z_0')
    z_steps = pm.Normal('z_steps', sigma=0.1, shape=N-1)
    zs = tt.concatenate([[z_0], z_steps])
    z = zs.cumsum()
    x = pm.Deterministic('x',pm.math.exp(z))
    mus = pm.Deterministic('mus', convolve(x))
    cases = pm.Poisson('cases', mu=mus, observed=y)
    trace = pm.sample(chains=1, tune=2000, draws=1000)
    pm.traceplot(trace)

続いて、サンプリングの結果を出力するコードと出力例を示す：

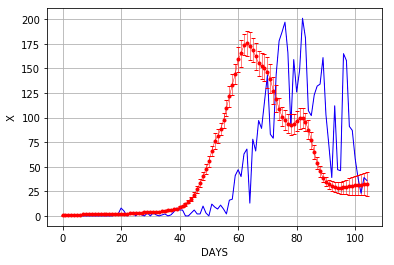
import matplotlib.pyplot as plt
xm = np.mean(trace['x'],axis=0)
xd = np.std(trace['x'],axis=0)

days=range(0,len(y))

plt.plot(days, y, color=(0.0,0.0,1.0), linewidth=1.0)
plt.errorbar(days, xm, yerr=xd, marker='.', color=(1.0,0.0,0.0), capthick=1, capsize=2, linewidth=0.5)

plt.xlabel('DAYS')
plt.ylabel('X')
plt.grid(True)
plt.show()

　練習：死亡者数を用いた推定

以下は、2020年2月24日以降の、日本でのCOVID-19による死亡者の累積データである。

# 2020年2月24日から5月19日までの日本の累積死亡者数
death_tolls=[
    1,1,1,1,1,1,1,1,1,1,1,1,1,3,4,5,5,6,6,6,6,6,6,6,7,9,12,15,19,21,22,24,28,29,31,
    33,35,36,41,42,43,45,46,49,52,54,56,57,60,63,69,70,73,80,81,85,88,94,98,102,109,
    119,136,148,154,161,171,186,277,287,317,334,348,351,376,389,415,432,458,492,510,
    521,543,551,557,600,613,621,643,668,687,710,725,744,749,763
]

これを元に、感染から死亡までの日数や致死率などに仮定を設けて、感染日ごとの感染者数を推定してみなさい。