統計モデルの比較
このページでは、モデルの「良さ」の比較について考えてみる。
パラメーター最尤値と尤度のバイアス
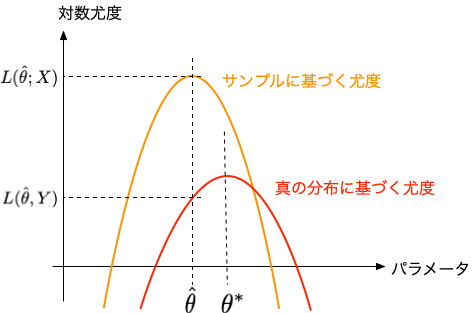
$g(y)$が真の分布、$f(x)$がモデルの分布。
ある確率分布 $g(x) $ に従っている独立なサンプル $x_1, x_2, \cdots, x_N$ が得られたとしよう。 そのデータを、$k$個のパラメータの組 $\theta_1, \theta_2, \cdots, \theta_k$ を持つような分布関数 $f(x ; \{\theta\} )$ で表現したい。 以下では、混乱が生じない限り、パラメータの組を単に $\theta$ と表記することにする。
そのための自然な発想として、対数尤度の平均 $$ L(\theta ; X) = \frac{1}{N} \sum_{\ell=1}^N \log f(x_\ell ; \theta) \tag{1} $$ を最大化するような $\theta$ を選べば良さそうである。すなわち $$ \frac{\partial}{\partial \theta_i} L(\hat\theta ; X) =0 \tag{2} $$ となるようなパラメータの組 $\hat{\theta}$ を選べばよさそうだ。
ところが、データは、サンプリングの都度異なるので、最尤推定したパラメータも、確率的に変動する。 $f$という分布(モデル)を仮定した下での「真の」パラメータは、 $$ L(\theta ; Y) = E_Y[ \log f(y ; \theta ) ] = \int g(y) \log f(y ; \theta ) \, dy \tag{3} $$ を最大化するような値であって、 $$ \frac{\partial}{\partial \theta_i} L(\theta^* ; Y) =0 \tag{4} $$ となるようなパラメータの組を $ \theta^* $ と書くことにする。 そして、$N \to \infty$ の極限では、両者は一致する(そのような場合を考える)。
では、$L(\hat\theta ; X)$ ができるだけ大きくなるようなモデル $f(x)$ が最善のモデルと言えるのだろうか? 統計理論の教えるところによれば、分布関数 $g(y)$ と $f(x)$ の隔たり具合(「距離」)は、 カルバック・ライブラー情報量(Kullback-Leibler information) $$ \begin{eqnarray} KL(g;f) = \int g(x) \log\left(\frac{g(x)}{f(x)} \right) \, dx \\ = \int g(x) \log g(x) \, dx - \int g(x) \log f(x) \, dx \end{eqnarray} $$ を客観的な指標として比較すべきである($\textrm{KL} \ge 0$で、両者が一致する場合のみ $\textrm{KL}=0$となる)。 そうすると、最大化しなければならないのは、上式の第2項に対応する $$ L(\hat\theta ; Y) = \int g(\hat\theta ; y) \log f(\hat\theta ; y) dy = E_Y\left[ \log f(y ; \hat{\theta} ) \right] \tag{5} $$ ということになる。
一方、この $L(\hat\theta ; Y)$ と、サンプル平均として求めた尤度 $L(\hat{\theta} ; X)$ との間には、 $N \to \infty$ でも0にならない偏差(バイアス)が存在することが知られている。
パラメーターのばらつき具合
サンプルから求めたパラメータ$\hat\theta$は、真の分布に対して尤度を最大とするパラメータ値$\theta^*$の周りでどのようにばらついているのだろうか。
平均対数尤度の微分を、$\theta^*$ の周りで展開すると、以下のようになる。 $$ \frac{\partial}{\partial \theta_i} L(\hat{\theta} ; X) = \frac{\partial}{\partial \theta_i} L(\theta^* ; X) + \sum_j^k \frac{\partial^2 L( \theta^* ; X)}{\partial \theta_j \partial \theta_i} (\hat{\theta}_j - \theta^*_j) + \cdots \tag{6} $$ ここで、定義から上式の左辺は0である。
以下で用いるため、行列 $A$ の各成分を $$ A_{ij} = - \frac{\partial^2 \log f(x; \theta^*)}{\partial \theta_j \partial \theta_i} $$ とおいて、 $$ \frac{\partial^2 L(\theta^* ; X)}{\partial \theta_j \partial \theta_i} = - E_X\left[ A \right] $$ と表しておく。また、ベクトル $\boldsymbol{b}$ の成分 $$ b_{i} = \frac{\partial}{\partial \theta_i} L(\theta^* ; X) $$ とおき、パラメータもベクトル表記 $$ \boldsymbol\theta = (\theta_1, \theta_2, \cdots, \theta_k)^\top $$ すると (6)式は $$ E_X[A] (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) = \boldsymbol{b} \tag{7} $$ と書ける。
ここで、 $$ b_i = \frac{1}{N} \sum_{\ell=1}^N \frac{\partial \log f(x_\ell ; \boldsymbol\theta^* )}{\partial \theta_i} \tag{8} $$ は、$N$個の独立な確率変数の和の形をしているので、中心極限定理から正規分布に漸近することが分かる。 その平均 $E_X[b_i]$ は0で、分散・共分散行列の $i,j$ 成分は $$ E_X[ b_i b_j ] = \frac{1}{N} \; E_X \left[ \frac{\partial \log f(x ; \boldsymbol\theta^* )}{\partial \theta_i} \frac{\partial \log f(x ; \boldsymbol\theta^* )}{\partial \theta_j} \right] = \frac{1}{N} E_X[ B ] \tag{9} $$ となる。 ここで、行列$B$の成分を $$ B_{ij} = \frac{\partial \log f(x ; \boldsymbol\theta^* )}{\partial \theta_i} \frac{\partial \log f(x ; \boldsymbol\theta^* )}{\partial \theta_j} $$ と置いた。
(7)式から $$ \hat{\boldsymbol\theta} - \boldsymbol\theta^* = E_X[A]^{-1} \boldsymbol{b} $$ であるから、$\hat{\boldsymbol\theta} - \boldsymbol\theta^*$ の分散・共分散行列は $$ E_X\left[ (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top \right] = \; E_X[A]^{-1} \, E_X[\boldsymbol{b} \boldsymbol{b}^\top] \, \left(E_X[A]^{-1}\right)^\top = \frac{1}{N} \; E_X[A]^{-1} \, E_X[B] \, E_X[A]^{-1} \tag{10} $$ となる。
$N$が十分大きければ、$X$についての平均は$Y$についてのそれに代えられるので(大数の法則) $$ E_X\left[ (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top \right] \approx \frac{1}{N} \; E_Y[A]^{-1} \, E_Y[B] \, E_Y[A]^{-1} $$
対数尤度のバイアス量の見積もり
データから推定したパラメータの組 $\{ \hat\theta\}$ から導出される尤度の差の平均量 $$ C = E_X\left[ L(\hat\theta(X) ; Y) - L(\hat\theta(X) ; X) \right] \tag{11} $$ を考える。ここで、$\hat\theta$はサンプル$X$から計算される量であることめ明示するため $\hat\theta(X)$ と表記した。
ここで、(11)式を $$ \begin{eqnarray} E_X\left[ L(\hat\theta(X) ; Y ) - L(\theta^* ; Y ) \right]\\ + E_X\left[ L(\theta^* ; Y ) - L(\theta^* ; X ) \right] \\ + E_X\left[ L(\theta^* ; X ) - L(\hat\theta(X) ; X) \right] \end{eqnarray} \tag{12} $$ と書き直し、1行目を $C_1$、2行目を $C_2$, 3行目を $C_3$ とする。 言うまでもなく、$C = C_1 + C_2 + C_3$ である。
$C_1$の評価
対数尤度を$\theta^*$の周りでテイラー展開すると $$ \begin{eqnarray} E_Y\left[ \log f(y ; \hat\theta(X) ) \right] = E_Y\left[ \log f(y ; \theta^* ) \right] + \sum_{i=1}^k \frac{\partial E_Y\left[\log f(y ; \theta^* ) \right]}{\partial \theta_i} (\theta(X)_i - \theta^*_i) \\ + \frac{1}{2} \sum_i \sum_j \frac{\partial^2 E_Y\left[\log f(y ; \theta^* ) \right]}{\partial \theta_i \partial \theta_j} (\theta(X)_i - \theta^*_i) (\theta(X)_j - \theta^*_j) + \cdots \end{eqnarray} \tag{13} $$ を得る。 ここで、$\theta^*$の定義より、右辺2項目(一階微分の項)は0となる。 上式を、対称行列 $$ J = - E_Y\left[ \frac{\partial^2 \log f(y ; \theta^* ) }{\partial \theta_i \partial \theta_j} \right] \tag{14} $$ を使って整理すると、 $$ L(\hat\theta(X) ; Y) - L(\theta^* ; Y ) \approx - \frac{1}{2} (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top J (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) \tag{15} $$ となる。
trace()は行列の対角要素の和(跡,トレース)。
$\boldsymbol{x}$をベクトル、$A$を対称行列とすると、次の関係が成り立つ: $$ \boldsymbol{x}^\top A \boldsymbol{x} = \textrm{trace}(A \boldsymbol{x} \boldsymbol{x}^\top) $$
右辺の平均を求めるために、まず、以下の計算をおこなう。 $$ \begin{eqnarray} E_X\left[ (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top J (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)\right] = E_X\left[ \textrm{trace}(J (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top ) \right] \\ =\textrm{trace} \left( J \; E_X\left[ (\hat{\boldsymbol\theta} - \boldsymbol\theta^*) (\hat{\boldsymbol\theta} - \boldsymbol\theta^*)^\top \right] \right) \\ \approx \frac{1}{N} \; \textrm{trace} \left( J \; E_Y[A]^{-1} \, E_Y[B] \, E_Y[A]^{-1} \right) \end{eqnarray} \tag{16} $$
ここで、$E_Y[A] = J$、すなわち $E_Y[A]^{-1} = J^{-1}$ に他ならないこと、そして、 $$ I = E_Y[B] = E_Y\left[ \frac{\partial \log f(y ; \boldsymbol\theta^* )}{\partial \theta_i} \frac{\partial \log f(y ; \boldsymbol\theta^* )}{\partial \theta_j} \right] \tag{17} $$ と改めて置き直すことで、(16)式は $$ = \frac{1}{N} \textrm{trace} \left(I \, J^{-1} \right) \tag{18} $$ となる。
さらに、$I$と$J$はFisher情報行列の異なる表現に他ならない($I=J$)から、結局 $$ = \frac{1}{N} \textrm{trace}(E) = \frac{k}{N} \tag{19} $$ を得る($E$は単位行列)。
以上をまとめると、$N \to \infty$ での $C_1$ の見積もりとして $$ C_1 = E_X\left[ L(\hat\theta(X) ; Y) - L(\theta^* ; Y ) \right] \approx -\frac{k}{2N} \tag{20} $$ が得られた。
$C_2$の評価
すでに、これまでの計算でも仮定されていたとおり、$X$は$Y$からのサンプルであるから、$N \to \infty$ では $$ C_2 = E_X\left[ L(\theta^* ; Y ) - L(\theta^* ; X ) \right] \to 0 \tag{21} $$ となる。
$C_3$の評価
$C_1$と同様に評価にすると、 $$ C_3 = E_X\left[ L(\theta^* ; X ) - L(\hat\theta(X) ; X) \right] \approx -\frac{k}{2N} \tag{22} $$ を示すことができる(確認せよ)。
以上から、全体的なバイアスの量 $$ C = C_1 + C_2 + C_3 = - \frac{k}{N} \tag{23} $$ が得られた。
赤池情報量基準(AIC)
前節までの結果から、 十分サンプル数が多く、各サンプルが独立であるような場合、サンプルから推定したパラメータから計算した対数尤度にはバイアスが含まれており、 その母平均は $$ L(\hat\theta(X) ;Y) = L(\hat\theta(X) ; X) - \frac{k}{N} = \frac{1}{N} \left\{ \sum_{\ell=1}^N \log f(x_\ell ; \hat\theta) - k \right\} \tag{24} $$ と見積もられる。ここで、$k$はパラメータの個数である。
尤度の最大値 $\hat\theta$ を求め、それを用いて$X$から尤度を計算する際に$k$個の拘束条件を課していることになる。 それら$k$個の自由度が減った分だけの補正が生じ、その値を(いくつかの仮定の下に)評価すると、上記のような結果になる、というわけである。
上式のカッコ内の量を-2倍した量は、赤池情報量基準(AIC)と呼ばれる: $$ \textrm{AIC} = - 2 \sum_{\ell=1}^N \log f(x_\ell ; \hat\theta) + 2 k \tag{25} $$ AICが小さいほど、「適切な」モデルであると考えられる。 パラメータの数を増やせば、それだけデータをよくフィッティングできる一方で、AICでは$2k$だけのペナルティが生じるので、 尤度の最大値とのバランスの中で、適切なモデル ($f(\cdot;\theta)$) を決めるための判断材料となる。
現実のデータに適用するに際しては、いくつかの改良版の基準が提案されているので、ここから先は専門書などに当たること。
SciPyを使った連続分布のAICの計算
SciPyを使うと、代表的な連続確率分布について、比較的簡単に統計量を計算することができる。 以下のPythonコードは、COVID-19のserial lengthの分析で使われているデータを用い、いくつかの確率分布についてAICを比較した例である。
パラメータの最尤推定はfit()関数を使って行うことができる。
変量Xは (x - loc)/scale のように、パラメータlocとscaleによって変換されるが、
フィッティングの際、それらをある値に固定したい場合は、それぞれ、floc=値、fscale=値のように指定すればよい。
各分布についてのパラメータの個数や意味については
scipy.statsのマニュアル を参照のこと。
サンプルに対する確率の対数を求める stats.poisson.logpmf() 関数や stats.norm.logpdf() は、
配列データを与えると配列を返すので、numpy.sum()でその総和を取って対数尤度を求めている。
from scipy import stats
import numpy as np
length=[3, 2, 4, 2, 2, 1, 4, 2, 10, 4, 3, 4, 4, 3, 3, 9, 9, 3, 4, 3, 9, 4, 5, 9, 7, 7, 3, 7]
mu = np.mean(length)
logL_poisson = np.sum(stats.poisson.logpmf(length, mu=mu))
aic_poisson = -2*logL_poisson + 2*1
print('AIC(POISSON)=',aic_poisson)
params_norm = stats.norm.fit(length)
logL_norm = np.sum( stats.norm.logpdf(length, loc=params_norm[0], scale=params_norm[1]) )
aic_norm = -2*logL_norm + 2*2
print('AIC(NORMAL)=',aic_norm)
params_gamma = stats.gamma.fit(length,floc=0)
logL_gamma = np.sum( stats.gamma.logpdf(length, params_gamma[0], loc=params_gamma[1], scale=params_gamma[2]) )
aic_gamma = -2*logL_gamma + 2*2
print('AIC(GAMMA)=',aic_gamma)
params_lognorm = stats.lognorm.fit(length,floc=0)
logL_lognorm = np.sum( stats.lognorm.logpdf(length, params_lognorm[0], loc=params_lognorm[1], scale=params_lognorm[2]) )
aic_lognorm = -2*logL_lognorm + 2*2
print('AIC(LOGNORM)=',aic_lognorm)
params_weibull = stats.weibull_min.fit(length,floc=0)
logL_weibull = np.sum( stats.weibull_min.logpdf(length, params_weibull[0], loc=params_weibull[1], scale=params_weibull[2]) )
aic_weibull = -2*logL_weibull + 2*2
print('AIC(WEIBULL)=',aic_weibull)
 練習:文長のモデルの比較
練習:文長のモデルの比較
夏目漱石の「こころ」の文の長さのデータをこちらに用意した。 文の長さが確率的に生成されていると仮定(単純化)した場合、どのようなどのような確率分布で表現するのがよいか、検討してみなさい。
最小二乗法による回帰曲線
データ点の組 $(x_i, y_i)$ を表すモデルが、パラメータを含む関数 $h(x;\theta)$ と、平均0、分散 $\sigma^2$ の正規分布に従うゆらぎ $\xi$ を使って、 $$ y_i = h(x_i ; \theta) + \xi $$ のように表されるとしよう。
データ点の数を$N$とすると、モデルからの残差の二乗和 $$ \sum_i^N (y_i - h(x_i ; \theta) )^2 $$ を最小化するようなパラメータを$\hat\theta$を与えると、対数尤度を最大化できる(最小二乗法)。 そのときの対数尤度は $$ L(\hat\theta, \hat\sigma ; \{x,y\}) = - \frac{N}{2} \log(2 \pi {\hat\sigma}^2) - \frac{1}{2 {\hat\sigma}^2} \sum_{i=1}^N (y_i - h(x_i ; \hat\theta) )^2 $$ となる。
分散の最尤推定値は、不偏分散とはならない点に注意。 実際に $\frac{\partial L}{\partial (\sigma^2)}=0$ を計算して確かめてみよ。
ここで、分散の最尤推定値は $$ {\hat\sigma}^2 = \frac{1}{N} \sum_{i=1}^N (y_i - h(x_i ; \theta) )^2 $$ になるから、最大対数尤度は、 $$ L(\hat\theta, \hat\sigma) = - \frac{1}{2} \left[ \log(2 \pi) + \log({\hat\sigma}^2) + 1 \right] $$ と書ける。
モデル関数のパラメータ$\theta$の個数を$m$とすれば、ゆらぎの分散 $\sigma^2$ の分を加え、モデル全体のパラメータは $m+1$ ある勘定になるから、 AICは $$ \textrm{AIC} = N \left[ \log(2 \pi) + \log({\hat\sigma}^2) + 1 \right] + 2\times(m+1) $$ となる。
用いたデータは、Rのサンプルデータ(cars)に基づいている。
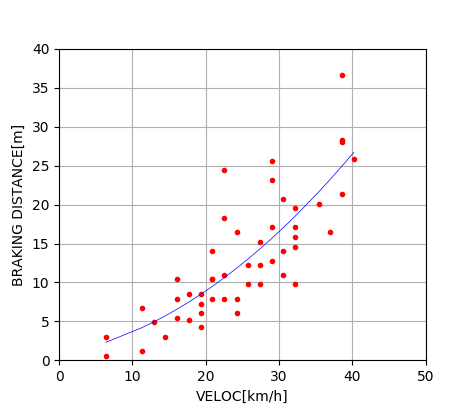
以下は、自動車の車速 $x$ と制動距離 $y=h(x)$ の関係を3通りの多項式 $$ \begin{eqnarray} h_1(x) = a_1 x + a_0 \\ h_2(x) = a_2 x^2 + a_1 x + a_0 \\ h_3(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0 \\ \end{eqnarray} $$ でモデル化し、(古い時代の)実測データからそれぞれのAICを計算するコードの例である。
実際にコードを実行すると、二次関数の場合にAICが最も小さくなることがわかる。 自動車の運動エネルギーは速度の2乗に比例する一方で、制動力(摩擦力)が一定とすると、制動で失われるエネルギーは(力)$\times$ (距離)に等しいから、 制動距離は速度の二乗に比例するはずである。 その点で、AICによるモデル比較の結果は妥当と解釈できる。
コードの補足:
numpy.polyfit()関数は、データの組から最小二乗法でパラメータの組(上記の$a_i$)を計算する。
numpy.poly1d()は、与えられたパラメータの組を元に、多項式関数を生成する。
# coding: utf-8
import scipy
import numpy as np
import matplotlib.pyplot as plt
data = np.array([
[6.4,0.6],[6.4,3.0],[11.3,1.2],[11.3,6.7],[12.9,4.9],[14.5,3.0],[16.1,5.5],[16.1,7.9],
[16.1,10.4],[17.7,5.2],[17.7,8.5],[19.3,4.3],[19.3,6.1],[19.3,7.3],[19.3,8.5],
[20.9,7.9],[20.9,10.4],[20.9,10.4],[20.9,14.0],[22.5,7.9],[22.5,11.0],[22.5,18.3],
[22.5,24.4],[24.2,6.1],[24.2,7.9],[24.2,16.5],[25.8,9.8],[25.8,12.2],[27.4,9.8],
[27.4,12.2],[27.4,15.2],[29.0,12.8],[29.0,17.1],[29.0,23.2],[29.0,25.6],[30.6,11.0],
[30.6,14.0],[30.6,20.7],[32.2,9.8],[32.2,14.6],[32.2,15.8],[32.2,17.1],[32.2,19.5],
[35.4,20.1],[37.0,16.5],[38.6,21.3],[38.6,28.0],[38.6,28.3],[38.6,36.6],[40.2,25.9]])
n=data.shape[0]
veloc = data[:,0]
dist = data[:,1]
param1 = np.polyfit(veloc, dist, 1)
param2 = np.polyfit(veloc, dist, 2)
param3 = np.polyfit(veloc, dist, 3)
func1 = np.poly1d(param1)
func2 = np.poly1d(param2)
func3 = np.poly1d(param3)
rss_1 = np.sum( np.square(func1(veloc)-dist) ) / n
rss_2 = np.sum( np.square(func2(veloc)-dist) ) / n
rss_3 = np.sum( np.square(func3(veloc)-dist) ) / n
aic_1 = n * (np.log(2*np.pi) + np.log(rss_1) + 1) + 2*(2+1)
aic_2 = n * (np.log(2*np.pi) + np.log(rss_2) + 1) + 2*(3+1)
aic_3 = n * (np.log(2*np.pi) + np.log(rss_3) + 1) + 2*(4+1)
print('AIC(LINEAR FUNCTION):',aic_1)
print('AIC(QUADRATIC FUNCTION):',aic_2)
print('AIC(CUBIC FUNCTION):',aic_3)
plt.plot(veloc,dist, '.', color=(1.0,0,0.0), linewidth=1.0)
plt.xlabel('VELOC[km/h]')
plt.xlim(0,50)
plt.ylabel('BRAKING DISTANCE[m]')
plt.ylim(0,40)
plt.grid(True)
plt.show()
コードを少し変更して、データ点に加え、二次関数でのフィッティング結果もプロットした例。
 練習:燃費と車重の関係
練習:燃費と車重の関係
データファイル:mtcars-mpg-wt.txt
(Rのサンプルデータ mtcars から作成)
複数の自家用車についての燃費(マイル/ガロン)と車重(単位:1000ポンド)のデータをこちらに 用意した。
AICを用いて、両者の関係を表すモデルについて考察してみなさい。