Pythonプログラミング（カルマンフィルター・その1）

カルマンフィルター（その１）

このページでは、カルマンフィルターによる推定について考えてみる。

「トロッコ問題」

AIの倫理等を巡ってよく取り上げられるトロッコ問題ではなく、トロッコの運動そもものを観測から推定する方法について考えてみたい。

時刻$t$でのトロッコの真の位置を$x(t)$, 速度を$v(t)$としよう。我々は各時刻でのトロッコの位置を観測することで、$z(t)$がデータとして得られる。

状態モデル中で加速（揺らぎ）の項に$\sqrt{\Delta}$が現れている理由についてはこちらを参照のこと。

時刻$t$での加速度を$a(t)$とし、 $a(t)$ は「見えざる力」によってランダムに変動する（各時刻で独立で、平均0のガウス分布に従う）と仮定すると、十分に小さな時間間隔$\Delta$後のトロッコの位置と速度は $$ \begin{eqnarray} x(t+\Delta) & = & x(t) + v(t) \Delta\\ v(t+\Delta) & = & v(t) + a(t) \sqrt{\Delta} \end{eqnarray} $$ のように変化するはずである。ここで$\Delta$より高次の項は省略。そして、これらを系の状態空間モデル(state space model)と考える。

他方で、観測するのは、実際の位置に計測誤差$b(t)$を加えた $$ z(t) = x(t) + b(t) $$ であると考える（観測モデル: observation model）。そして、$b(t)$についても、各時刻で独立で、平均0のガウス分布に従うと仮定する。

トロッコの運動が状態空間モデルに従うという仮定のもとで、観測時系列$\{ z(t) \}$から位置と速度（$x(t), v(t)$）を推定するのが、ここでの問題設定である。

位置と速度の予測値と分散の予測

時刻$t$での状態に基づいた時刻$t+\Delta$での位置の速度の予測値（期待値）を $\hat{x}(t+\Delta | t)$ および $\hat{v}(t+\Delta | t)$ で表すことにしよう。ここでゆらぎや誤差についての平均を$\left\langle \cdot \right\rangle$で表すことにすると時刻 $t+\Delta$での予測値は、 $$ \begin{eqnarray} \hat{x}(t + \Delta | t) & = & \left\langle x(t) + v(t) \Delta \right\rangle = \hat{x}(t) + \hat{v}(t) \Delta \\ \hat{v}(t + \Delta | t) & = & \left\langle v(t) + a(t) \sqrt{\Delta} \right\rangle = \hat{v}(t) \end{eqnarray} $$ となる。

ここで、式が煩雑になるのを避けるため、予測値については $\hat{x}(t+\Delta | t) \rightarrow \hat{x}(t+\Delta)$ のように、「〜の条件下で」の箇所の表記を省略する場合がある（以下同様）。また、$a(t)$は平均0で他の量と無相関な変動なので、別の量$X(t)$との積の平均は $$ \left\langle X(t) \, a(t) \right\rangle = \left\langle X(t) \right\rangle \, \left\langle a(t) \right\rangle = 0 $$ となることを用いる。

次に、予測値からの内部状態の偏差 $$ \begin{eqnarray} \delta x(t) & \equiv & x(t) - \hat{x}(t) \\ \delta v(t) & \equiv & v(t) - \hat{v}(t) \end{eqnarray} $$ と定義し、 $t+\Delta$での共分散行列の予測値 $$ \hat{S}(t+\Delta) = \begin{pmatrix} \left\langle \delta x(t+\Delta) \, \delta x(t+\Delta) \right\rangle & \left\langle \delta x(t+\Delta) \, \delta v(t+\Delta) \right\rangle \\ \left\langle \delta x(t+\Delta) \, \delta v(t+\Delta) \right\rangle & \left\langle \delta v(t+\Delta) \, \delta v(t+\Delta) \right\rangle \end{pmatrix} $$ を評価してみよう。配列要素はそれぞれ $$ \begin{eqnarray} \hat{S}_{xx}(t+\Delta) \equiv \left\langle \delta x(t+\Delta) \, \delta x(t+\Delta) \right\rangle = \left\langle \left(x(t) + v(t) \Delta - (\hat{x}(t) + \hat{v}(t) \Delta)\right)^2 \right\rangle \\ = \left\langle (x(t)-\hat{x}(t))^2 \right\rangle + 2 \left\langle (x(t)-\hat{x}(t)) (v(t)-\hat{v}(t)) \right\rangle \Delta + \left\langle (v(t)-\hat{v}(t))^2 \right\rangle (\Delta)^2 \end{eqnarray} $$ $$ \begin{eqnarray} \hat{S}_{xv}(t+\Delta) \equiv & \left\langle \delta x(t+\Delta) \, \delta v(t+\Delta) \right\rangle = \left\langle \left(x(t) + v(t) \Delta - (\hat{x}(t) + \hat{v}(t) \Delta)\right) \left(v(t) + a(t) \sqrt{\Delta} - \hat{v}(t)\right) \right\rangle \\ & = \left\langle (x(t)-\hat{x}(t)) (v(t)-\hat{v}(t)) \right\rangle + \left\langle (v(t)-\hat{v}(t))^2 \right\rangle \Delta \end{eqnarray} $$ $$ \begin{eqnarray} \hat{S}_{vv}(t+\Delta) \equiv & \left\langle \delta v(t +\Delta) \, \delta v(t+\Delta) \right\rangle = \left\langle \left( v(t) + a(t) \sqrt{\Delta} - \hat{v}(t) \right)^2 \right\rangle \\ & = \left\langle \left( v(t) - \hat{v}(t) \right)^2 \right\rangle + \left\langle a(t)^2 \right\rangle \Delta \end{eqnarray} $$ となるので、$R(t) = \left\langle a(t)^2 \right\rangle$ と置いて、共分散行列についての漸化式 $$ \begin{eqnarray} \hat{S}_{xx}(t + \Delta) & = & \hat{S}_{xx}(t) + 2 \hat{S}_{xv}(t) \Delta + \hat{S}_{vv} (\Delta)^2\\ \hat{S}_{xv}(t + \Delta) & = & \hat{S}_{xv}(t) + \hat{S}_{vv}(t) \Delta \\ \hat{S}_{vv}(t + \Delta) & = & \hat{S}_{vv}(t) + R(t) \Delta \end{eqnarray} $$ が得られる。

観測位置の偏差

観測量の予測値からの偏差は $$ \delta z(t|t-\Delta) \equiv z(t) - \hat{z}(t|t-\Delta) = x(t) + b(t) - \hat{x}(t|t-\Delta) $$ となり、ここでも $\hat{x}(t|t-\Delta) \rightarrow \hat{x}(t)$のように表記を省略すると、その分散は $$ \hat{V}(t) = \left\langle \left( x(t) + b(t) - \hat{x}(t) \right)^2 \right\rangle = \left\langle \left( x(t) - \hat{x}(t) \right)^2 \right\rangle + \left\langle b(t)^2 \right\rangle = \hat{S}_{xx}(t) + Q(t) $$ となる。ここで $Q(t) = \left\langle b(t)^2 \right\rangle$ と置いた。

観測による予測値の修正

ひとつステップ前 $t-\Delta$ の内部状態を用いて $t$ での内部状態を予測した値は、当然、ある程度「外れて」いるはずである。他方で、時刻$t$では新たな情報として、トロッコの位置が観測誤差と伴って得られている。そこで、観測情報に基づいて、内部状態の予測値に修正を加えるのが良さそうである。もし、実際の観測位置がその予測値と全く同じであれば、内部状態の予測もうまく行っているはずであるから、内部状態の予測値をそのまま採用すれば良い。他方で、観測位置がその予測値の差（$\delta z(t|t-\Delta)$）が大きければ、それに応じて線形に、内部状態の予測値を修正することにしよう。こうした方式はカルマンフィルターと呼ばれている。

具体的には $$ \begin{eqnarray} \tilde{x}(t) & = & \hat{x}(t|t-\Delta) + k_x \left[ z(t) - \hat{z}(t|t-\Delta)\right] \\ \tilde{v}(t) & = & \hat{v}(t|t-\Delta) + k_y \left[ z(t) - \hat{z}(t|t-\Delta)\right] \\ \end{eqnarray} $$ のように、比例係数（カルマンゲインという） $k_x, k_v$ を与える。

では、これらのカルマンゲインはどのように決めたら良いだろうか。それには、修正予測値 $\tilde{x}(t),\tilde{v}(t)$ と内部状態 $x(t), v(t)$ との二乗差の平均 $$ d(k_x,k_y) = \left\langle \left( x(t) - \tilde{x}(t) \right)^2 + \left( v(t) - \tilde{v}(t) \right)^2 \right\rangle $$ が最小になるような$k_x, k_v$が求められれば良さそうである。

そこで上式をカルマンゲインで偏微分して0と置くと $$ \begin{eqnarray} \frac{\partial d(k_x,k_y)}{\partial k_x} & = & - 2 \left\langle (x(t) - \hat{x}(t)) ( z(t) - \hat{z}(t)) \right\rangle + 2 k_x \left\langle (z(t) - \hat{z}(t))^2 \right\rangle = 0 \\ \frac{\partial d(k_x,k_y)}{\partial k_v} & = & - 2 \left\langle (v(t) - \hat{v}(t)) ( z(t) - \hat{z}(t)) \right\rangle + 2 k_v \left\langle (z(t) - \hat{z}(t))^2 \right\rangle = 0 \end{eqnarray} $$ であるから、 $$ \begin{eqnarray} k_x & = & \frac{\left\langle (x(t) - \hat{x}(t)) ( z(t) - \hat{z}(t)) \right\rangle}{\left\langle (z(t) - \hat{z}(t))^2 \right\rangle} \\ k_v & = & \frac{\left\langle (v(t) - \hat{v}(t)) ( z(t) - \hat{z}(t)) \right\rangle}{\left\langle (z(t) - \hat{z}(t))^2 \right\rangle} \end{eqnarray} $$ となる。

ここで、 $$ z(t) - \hat{z}(t|t-\Delta) = x(t) - b(t) - \hat{x}(t|t-\Delta) $$ であるから $$ \begin{eqnarray} \left\langle (x(t) - \hat{x}(t)) ( z(t) - \hat{z}(t)) \right\rangle = \left\langle (x(t) - \hat{x}(t))^2 \right\rangle - \left\langle (x(t) - \hat{x}(t)) b(t) \right\rangle \\ = \left\langle (x(t) - \hat{x}(t))^2 \right\rangle = \hat{S}_{xx}(t|t-\Delta) \end{eqnarray} $$ 同様に、 $$ \left\langle (v(t) - \hat{v}(t)) ( z(t) - \hat{z}(t)) \right\rangle = \left\langle (v(t) - \hat{v}(t)) (x(t) - \hat{x}(t)) \right\rangle = \hat{S}_{xv}(t|t-\Delta) $$

また、 $$ \left\langle (z(t) - \hat{z}(t))^2 \right\rangle = \hat{S}_{xx}(t|t-\Delta) + Q(t) $$

トロッコ問題のアルゴリズム

以上をまとめると、各時刻のトロッコの観測位置$z(t)$を得ながら、内部状態モデルの変数を推定するアルゴリズムは以下のとおりとなる：

初期設定

内部状態の予測値 $\hat{x}(0), \hat{v}(0)$、および共分散行列の予測値 $\hat{S}$ の初期値を与える。

時刻 $t$ での観測値$z(t)$を取得し、内部状態の揺らぎの分散 $R(t)$と観測誤差の分散$Q(t)$を設定する。

カルマンゲインを求め、観測量をもとに予測値を修正する

カルマンゲインを $$ \begin{eqnarray} k_x & = & \frac{\hat{S}_{xx}(t|t-\Delta)}{\hat{S}_{xx}(t|t-\Delta) + Q(t)} \\ k_v & = & \frac{\hat{S}_{xv}(t|t-\Delta)}{\hat{S}_{xx}(t|t-\Delta) + Q(t)} \end{eqnarray} $$ と置く。$z(t)$の予測値が$\hat{z}(t) = \hat{x}(t|t-\Delta)$であることを思い出し、時刻$t$での内部状態の予測値 $$ \begin{eqnarray} \tilde{x}(t) & = & \hat{x}(t|t-\Delta) + k_x \left[ z(t) - \hat{x}(t|t-\Delta)\right] \\ \tilde{v}(t) & = & \hat{v}(t|t-\Delta) + k_v \left[ z(t) - \hat{x}(t|t-\Delta)\right] \\ \end{eqnarray} $$ で更新する。

共分散行列を修正する

修正された内部状態の予測値に基づいて共分散行列を更新する $$ \begin{eqnarray} \tilde{S}_{xx}(t)& = & \left\langle (x(t)-\tilde{x}(t))^2 \right\rangle \\ & = & \left\langle \left(x(t)-\hat{x}(t|t-\Delta) - k_x \left[ z(t) - \hat{z}(t|t-\Delta) \right] \right)^2 \right\rangle \\ & = & \left\langle \left(x(t)-\hat{x}(t|t-\Delta)\right)^2 \right\rangle - 2 {k_x} \left\langle \left(x(t)-\hat{x}(t|t-\Delta)\right) \left( x(t)+b(t)- \hat{x}(t|t-\Delta) \right) \right\rangle \\ & + & {k_x}^2 \left\langle \left( x(t)+b(t)- \hat{x}(t|t-\Delta) \right)^2 \right\rangle \\ & = & (1 - 2 k_x + {k_x}^2) \hat{S}_{xx}(t|t-\Delta) + {k_x}^2 Q(t)\\ \tilde{S}_{xv}(t) & = & \left\langle (x(t)-\tilde{x}(t)) (v(t)-\tilde{v}(t)) \right\rangle \\ & = & \hat{S}_{xv}(t|t-\Delta) - k_x \hat{S}_{xv}(t|t-\Delta) - k_v \hat{S}_{xx}(t|t-\Delta) + k_x k_v \hat{S}_{xx}(t|t-\Delta) \\ & = & (1 - k_x) \hat{S}_{xv}(t|t-\Delta) + k_v (k_x - 1) \hat{S}_{xx}(t|t-\Delta) + k_x k_v Q(t) \\ \tilde{S}_{vv}(t) & = & \left\langle (v(t)-\tilde{v}(t))^2 \right\rangle \\ & = & \hat{S}_{vv}(t|t-\Delta) - 2 k_v \hat{S}_{xv}(t|t-\Delta) + {k_v}^2 \hat{S}_{xx}(t|t-\Delta) + {k_v}^2 Q(t) \end{eqnarray} $$

上はえらく煩雑な式に見えるが、カルマンゲインを代入して整理すると $$ \begin{eqnarray} \tilde{S}_{xx}(t)& = & \hat{S}_{xx}(t|t-\Delta) - \frac{\hat{S}_{xx}(t|t-\Delta)^2}{\hat{S}_{xx}(t|t-\Delta) + Q(t)} \\ \tilde{S}_{xv}(t)& = & \hat{S}_{xv}(t|t-\Delta) - \frac{\hat{S}_{xx}(t|t-\Delta) \, \hat{S}_{xv}(t|t-\Delta) }{\hat{S}_{xx}(t|t-\Delta) + Q(t)} \\ \tilde{S}_{vv}(t)& = & \hat{S}_{vv}(t|t-\Delta) - \frac{\hat{S}_{xv}(t|t-\Delta)^2}{\hat{S}_{xx}(t|t-\Delta) + Q(t)} \end{eqnarray} $$ となり、式の形から、反復に伴い内部状態の分散の推定値 $\hat{S}$ は時間経過と共に単調に減少することがわかる。また、観測誤差の分散$Q(t)$が小さいほど、$\hat{S}$ もより小さくなるように調整される。

$\Delta$先の内部状態の予測値を求める

次の時間ステップの内部状態の予測値を更新する。 $$ \begin{eqnarray} \hat{x}(t+\Delta) & = & \tilde{x}(t) + \tilde{v}(t) \Delta \\ \hat{v}(t+\Delta) & = & \tilde{v}(t) \end{eqnarray} $$

$\Delta$先の共分散行列の予測値を求める

次の時間ステップの共分散行列の予測値を以下で更新する。 $$ \begin{eqnarray} \hat{S}_{xx}(t+\Delta) & = & \tilde{S}_{xx}(t) + 2 \tilde{S}_{xv}(t) \Delta + \tilde{S}_{vv} (\Delta)^2 \\ \hat{S}_{xv}(t+\Delta) & = & \tilde{S}_{xv}(t) + \tilde{S}_{vv}(t) \Delta \\ \hat{S}_{vv}(t + \Delta) & = & \tilde{S}_{vv}(t) + R(t) \Delta \end{eqnarray} $$

数値シミュレーション

上記のモデルをそのままPythonに翻訳したコードの例を示す。簡単のため、状態モデルのゆらぎと観測誤差は一定とした。

# coding: utf-8

import random
import math
import matplotlib.pyplot as plt

X=[ ]
V=[ ]
T=[ ]

XT=[ ]
XTERR=[ ]
ZT=[ ]

SXX=[ ]

x=0
v=1
t=0
dt = 0.1

xt=-1
vt=0
sxx=1
sxv=1
svv=1

while t<10:
    R=1.0
    Q=2.0

    zt = x + random.gauss(0,math.sqrt(Q))

    kx = sxx/(sxx+Q)
    kv = sxv/(sxx+Q)

    xt2 = xt + kx * (zt - xt)
    vt2 = vt + kv * (zt - xt)

    sxx2 = sxx - sxx**2/(sxx+Q)
    sxv2 = sxv - sxx*sxv/(sxx+Q)
    svv2 = svv - sxv**2/(sxx+Q)

    xt = xt2 + vt2 * dt
    vt = vt2

    T.append(t)
    X.append(x)
    XT.append(xt)
    ZT.append(zt)
    XTERR.append(math.sqrt(sxx2))
    SXX.append(sxx2)

    sxx = sxx2 + 2*sxv2*dt + svv2*dt**2 
    sxv = sxv2 + svv2*dt 
    svv = svv2 + R*dt
    
# update internal state
    at = random.gauss(0,math.sqrt(R))
    x = x + v * dt 
    v = v + at*math.sqrt(dt)
    t = t + dt        

plt.plot(T,X, color='blue', linewidth=1.0, label='State Model')
plt.errorbar(T,XT, yerr=XTERR, capsize=5, fmt='o', color='red', ecolor='orange',label='Estimate')
plt.plot(T,ZT, '*', color='green', linewidth=1.0, label='Observation')
plt.xlabel('T')
plt.ylabel('X')
plt.grid(True)
plt.legend()
plt.show()

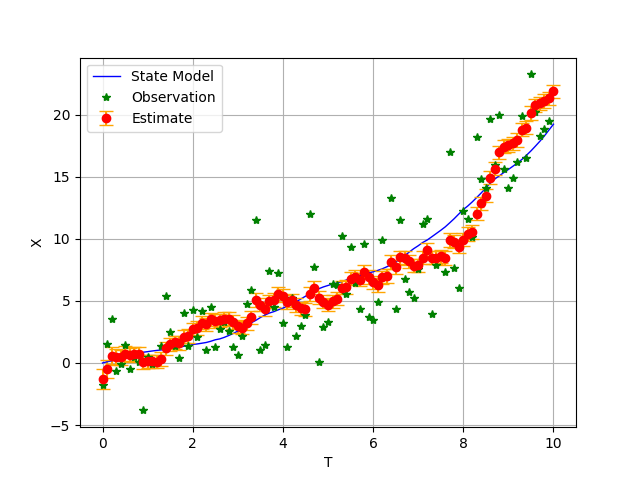
青い線が内部モデルの$x(t)$の変化、緑のアスタリスクが観測値である。観測値は誤差によって大きく散らばっているが、カルマンフィルターによる状態の推定値は、真値の近くに留まっている様子が判る。

　練習：ブラウン運動

こちらも参照のこと。

花粉やコロイド粒子などがブラウン運動する際の運動方程式は $$ \begin{eqnarray} \dot{x}(t) & = & v(t) \\ m \dot{v}(t) & = & -\gamma v(t) + \xi(t) \end{eqnarray} $$ のように表される。ここで、$m$は微粒子の質量、$\gamma$は流体からの受ける粘性抵抗の程度（摩擦）を表す係数、 $\xi(t)$は平均が0、分散が $$ \langle \xi(s) \xi(t) \rangle = 2 \gamma k_B T \delta(t-s) $$ （$k_B$はボルツマン定数、$T$は絶対温度）である。

簡単のため、$m=1, \gamma=1$、$2 \gamma k_B T = R$とおき、粒子の位置 $x(t)$ のみが観測可能として、カルマンフィルターのアルゴリズムを構成してみなさい。