地震の確率モデル

このページでは、地震の発生確率について考えてみる。

地震の統計的な側面

日本は世界でも特異的に地震の多い国である。複数のプレートが交錯し、定常的に歪みが蓄積され、体感できない小さな規模のものも含めると、揺れているのが常態と言ってもよいくらいである。

地震の規模の指標はマグニチュードと呼ばれ、地震によって開放されたエネルギー$E$を対数スケールで表現した値である。 地震のエネルギーは、断層が滑った規模を地震波の解析から推定して算出され、それを用いて（モーメント）マグニチュードは $$ M = \frac{2}{3} \log_{10} E - 10.7 \tag{1} $$ で定義されているので、$E$が1000倍になると、$\frac{2}{3} \times 3 = 2$、すなわちマグニチュードは2増加する （定数は、基準となるエネルギーを与える）。

地震の規模（マグニチュード）は、グーテンベルグ・リヒター則と呼ばれる経験的な統計則によく従うことが知られており、 マグニチュード$M$の地震が発生する頻度 $N$ は $$ \log_{10} N = a - b M \tag{2} $$ で表される。ここで$b$は凡そ1程度の値を取ることが知られている。 言い換えれば、マグニチュードが1少ない地震の発生頻度は10倍ということになる。 東日本大震災をもたらした東北地方太平洋沖地震クラスのM9の地震は、世界的な規模で見ると、約10年に1回程度の頻度で発生しているようである。 そうすると、M8クラスは毎年1回、M7は1年に10回程度、地球上のどこかで起こっている計算になる。

大きな地震の後には、しばらく余震が続くのは誰しも経験することである。 本震から 時間$t$ 後の余震の発生頻度を $n(t)$ とすると、大森則 $$ n(t) \propto \left( 1 + t/c \right)^{-p} \tag{3} $$ がよく成り立つ。ここで、$p$は、地震によって幅があるものの、1程度の値を取る。 本震直後はしばらく頻繁に余震が発生し、その後は、時間が10倍経過すれば10分の1程度のペースで余震の頻度は減少することになる。

これらの統計則は、現実のデータに驚くくらいよくフィットするにも関わらず、そうした振る舞いが生じる根本的な理由については、なお研究の途上である。

BPT分布

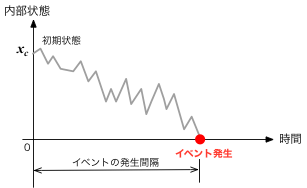
地震に限らず、内部状態がランダムに変化して、ある臨界的な値まで達するとイベントが発生し、初期状態にリセットされる、というプロセスは色々とありそうである。 そのような現象で、イベントとイベントの間隔はどのような確率分布に従っていると見るのが適切だろうか。

一点に落としたインクの広がりの様子

流れが無く、インクの分子が熱運動によって広がる（拡散）様子は拡散方程式によって記述される。 インクの分子のひとつひとつの運動を追うのではなく、全体的な数（濃度）の変化に着目し、 座標$x$、時刻$t$での濃度を $u(x,t)$ と置く。 すると拡散方程式は $$ \frac{\partial u(x,t)}{\partial t} = D \frac{\partial^2 u(x,t)}{\partial x^2} \tag{4} $$ となる。 ここで$D$はインクの広がりやすさを表す定数（拡散定数）である。

ここで、$u(x,t)$の$x$についてのフーリエ変換を $$ \hat{G}(k,t) = \int_{-\infty}^{\infty} u(x,t) e^{-i k x} dx \tag{5} $$ と置くと、拡散方程式は時間については簡単な常微分方程式 $$ \frac{d}{dt} \hat{G}(k, t) = - D k^2 \hat{G}(k,\omega) \tag{6} $$ になるから、これを解いて $$ \hat{G}(k, t) = A(k) \exp\left( - D k^2 t \right) \tag{7} $$ を得る。

ここで、「時刻0にインクを一点($x=x_c$)に落とした場合」を考え、初期条件をデルタ関数を使って $$ u(x_c, 0) = \delta(x-x_c) \tag{8} $$ と置くと $$ \frac{1}{2\pi} \int \hat{G}(k,0) e^{i k x} dk = \frac{1}{2 \pi} \int A(k) e^{i k x} d k = \delta(x-x_c) \tag{9} $$ であるから、デルタ関数のフーリエ変換による表現 $ \delta(x-a) = \frac{1}{2\pi} \int \exp(i (x-a) k) dk $ と見比べて $$ A(k) = e^{-i k x_c} \tag{10} $$ となる。

以上から、 $$ \hat{G}(k,t) = \exp\left( - D k^2 t - i k x_c \right) \tag{11} $$ が得られたので、これを$k$について逆フーリエ変換することで、$u(x,t)$が得られる： $$ \begin{eqnarray} u(x,t) & = & \frac{1}{2 \pi} \int \hat{G}(k,t) e^{i k x} dk \\ & = & \frac{1}{2 \pi} \int \exp\left[ - D t\left(k - \frac{i (x-x_c)}{2 D t}\right)^2 - \frac{(x-x_c)^2}{4 D t} \right] dk \\ & = & \frac{1}{2 \pi} \int \exp\left[ - D t\left(k - \frac{i (x-x_c)}{2 D t}\right)^2 \right] d k \; \exp\left( - \frac{(x-x_c)^2}{4 D t} \right) \\ & = & \frac{1}{\sqrt{4 \pi D t}} \exp\left( - \frac{(x-x_c)^2}{4 D t} \right) \end{eqnarray} \tag{12} $$ 一見複雑そうに見えるが、指数関数の中身を平方完成し、ガウス積分の性質 $\int_{-\infty}^{\infty} e^{-a(k-b)^2} dk = \sqrt{\pi/a}$ を使った以外、 特に難しい計算は行っていない点に注意。

完全な吸い取り紙を置いた場合

次に、座標 $x=0$ に「完全な」吸い取り紙が置かれている場合、インクがどれくらい吸い取られるかを考える。 そうすると、$x=0$では常に $$ u(0,t)=0 \tag{13} $$ が成り立ってなければならないことになるが、ちょっとしたトリックを使えば、そのような状況を簡単に再現できる。

最初にインクを垂らす点$x=x_c$のちょうど原点対称の場所に、「負の濃度の」インクを垂らす。 拡散方程式は線形なので、このように境界条件を満たすように解を重ね合わせることが可能である。 その結果、インクの濃度の時間発展は $$ u(x,t) = \frac{1}{\sqrt{4 \pi D t}} \exp\left( - \frac{(x-x_c)^2}{4 D t} \right) - \frac{1}{\sqrt{4 \pi D t}} \exp\left( - \frac{(x+x_c)^2}{4 D t} \right) \tag{14} $$ と表される。

原点の吸い取り紙から流れ「出す」インクの量は、原点での濃度勾配に比例し $$ J(t) = - D \frac{\partial u(0,t)}{\partial x} = - \frac{x_c}{\sqrt{4 \pi t^3} } \exp\left(-\frac{{x_c}^2}{4 D t} \right) \tag{15} $$ となる。

ここまでをまとめると、$x=x_c$を放たれた総量1のインクの分子は、時刻 $t$ に、時間あたり $$ \frac{x_c}{\sqrt{4 \pi D t^3}} \exp\left(-\frac{{x_c}^2}{4 D t} \right) \tag{16} $$ だけ原点に到来することになる。

BPT分布

同様に、インクの分子が何らかの外場を受けて、速度$v$でドリフトを伴いながらランダムウォークしている状況について同様の計算を行うと 時刻$t=0$に、$x=x_c$を出発した粒子が$x=0$に到着する確率分布は $$ p(t) = \frac{x_c}{\sqrt{4 \pi D t^3}} \exp\left(-\frac{ \left(x_c + v t \right)^2 }{4 D t} \right) \tag{17} $$ となり、BPT(Brownian Passage Time)分布、あるいは逆ガウス分布（inverse Gaussian distribution)と呼ばれている。

このBPT分布は、プレート型地震の間隔を議論する際に用いられている。 プレート運動によってある一定の割合で地下岩盤の歪が蓄積され、力学的な限界を超えると、大規模な破壊が生じ、地震として観測されるわけである。 ブラウン粒子の位置を地中の内部状態と思えば、初期状態（$x_c$）から始まって、ランダムな揺らぎを伴いながら時間と共に次第に歪みが生じ、 ある臨界的な状態（$x=0$）に至ると地震発生となる一連のプロセスを、少なくともその概容は捉えているように思われる （0から出発して$x_c$に至るプロセスのほうが考えやすいかもしれないが、同じことである）。

なお、文献等では、BPT分布を、2つのパラメータ $\lambda, \mu$を使って $$ f(t) = \sqrt{\frac{\lambda}{2\pi t^3}} \exp\left( - \frac{\lambda(t - \mu)^2}{2 \mu^2 t} \right) \tag{26} $$ と表すのが一般的である（Tweedieによる表現。$\mu$は平均）。

　練習：南海地震の発生間隔分布

ネット上に公開されている地震調査研究推進本部・地震調査委員会の文書 によれば、典型的なプレート間地震である南海地震は、これまでに

202.7
211.5
262.4
136.9
106.6
102.7
147.2
 92.0

の間隔（単位は年）で発生している。

地震の間隔がBPT分布に従うと仮定し、パラメータ$\mu$, $\lambda$を推定しなさい。

　ヒント

# coding: utf-8

from scipy import stats
import numpy as np

X = [202.7,211.5,262.4,136.9,106.6,102.7,147.2,92.0]

params_bpt = stats.invgauss.fit(X,floc=0)

print('mu=',params_bpt[0] * params_bpt[2])
print('lambda=', params_bpt[2])

　発展練習：南海地震の発生確率

最後に南海地震を観測したのは1946年12月であった。今年（2020年）まで73年が経過していることになる。 『今後$T$年以内に95%の確率で南海地震が発生する』という予想を立ててみなさい。

　ヒント