日付と時間
このページではPythonでの時間と日付の扱いについてまとめておく(ここはまだ書きかけ)。
コンピュータの時計
コンピュータの内部には独立した時計の機能がハードウェアとして組み込まれており、そこから日時を読み出したり、設定したりすることができるようになっている場合がほとんどである。こうしたコンピュータ内の時計は、一般的な時計と同様、水晶発振器など正確な時間間隔を刻む素子によって駆動されてはいるものの、単体では少しずつずれてしまう。
現在では、多くのコンピュータがネットワークに接続されているため、正確な時計を内蔵したサーバーに問い合わせることで、自らの時計を自動修正するようになっている場合が多い。 そのための標準的な手順がNTP(Network Time Protocol)である。 Windows 10では、Windowsの設定 → 時刻と言語 → 日付と時刻 を開き、「時刻を自動的に設定する」によって、NTPサーバーとの同期が行われる。 macOSの場合は、システム環境設定 → 日付と時刻 の「日付と時刻を自動的に設定」の項目がそれに相当する。 NTPサーバーは世界中に多数存在しており、OSの種類や地域毎に推奨されている設定に従う(通常は、適切なデフォルト値が設定されている)。
時刻の表現
時刻の自然な表現方法は、起点となる日時を設け、そこからの長さ(秒数)を数える方法である。 実際に多くのソフトウェア では、1970日1月1日午前0時を起点として、そこからの経過秒数によって時間を表現している(UNIX時間)。 ところが、実際の暦ではときおり閏秒が発生しているため、実際の経過秒数から日時を計算すると、暦とずれてしまう。 そこで、UNIX時間から日時を算出する場合には、その間のうるう秒を考慮して、暦と整合するよう計算するような仕組みが組み込まれているのが通常である。
従来型のハードウェアで多く用いられていた(符号付き)32ビット整数で秒数を表すと、2038年で、その表現できる最大値を超えてしまうため、旧型の情報通信機器の誤動作が懸念されている(2038年問題)
Pythonでの日付と時間の扱い
Pythonで日付と時間を扱う際には、標準的な機能である timeモジュールや datetimeモジュールが利用できる。
これらを使った、誕生日を入力すると、現在まで何日が経過したか、およびその時点のUnix時間を表示するコードの例を以下に示す:
# coding:utf-8
from datetime import datetime
birthday = input("input your birthday (yyyy/dd/mm):")
bd = datetime.strptime(birthday,'%Y/%m/%d')
now = datetime.now()
delta = now - bd
print("You lived",delta.days,"days since you were born.")
print("Current Unix time is",now.timestamp())
 解説: Pythonは人類滅亡をカウントダウンできるか
解説: Pythonは人類滅亡をカウントダウンできるか
Pythonのdatetimeモジュールで表現できる西暦の最大値は datetime.MAXYEARで得られる:
import datetime print(datetime.MAXYEAR)
実際にPython 3で実行すると 9999 と表示される。
また、Unix時間の秒数を符号付きの64ビット整数で表現したとすると、最大で $2^{63} = 9223372036854775808$ 秒、 それを年数に換算すると、約$2.9 \times 10^{11}$ 年で、これが現代のコンピュータで(秒精度で)計時できる最大値と言える。
人類滅亡までのカウントダウンプログラムを作成するとして、Pythonの処理系や現在のコンピュータはそれに必要な時間を扱うことができるのだろうか。そのためには、人類滅亡までの時間を見積もる必要がある。
例えば、核戦争による人類の危機を象徴的に表現した世界終末時計は、警鐘を鳴らすことが主な目的なので、その針は進んだり戻ったりしており、我々の残り時間の予測には使えそうもない。
ここから先は、定説というわけでは無いので、話半分で読んでください。
そこで、色々な事物の余命を推定したGottによる議論を少し焼き直して考察してみよう。
種の絶滅が何らかのランダムなイベント(パンデミックや環境の急激な変動等)で生じるとすれば、イベント間の時間間隔は(第0近似としては)指数分布に従うと考えるのが自然である(不安定原子核の崩壊のようなもの、と、考える)。 人類に対してそういったイベントがどれくらいの頻度で生じるかは不明であるが、その平均間隔を$L$万年と置き、 種の誕生から$T$万年目にイベントが実際に生じて絶滅する確率を $$ P(T) = \frac{1}{L} \exp\left( - T \big/ L \right) \tag{1} $$ と書いてみる。
人類に近いネアンデルタール人は40万年程度の期間で絶滅したらしい。一方、チンパンジーは約500万年前に、系統樹の上で、枝分かれしたと言われ、現在まで生存している。とすれば、上記の$L$は、少なくとも100万年から1000万年程度かそれ以上と考えて良さそうである。
次に、人類誕生から、我々は$t$万年目に差し掛かっているとする。 我々がこの瞬間に生を受けたのは全く偶然と考えるほか無さそうであるから、 種の寿命$T$を知っているとき、その確率は $$ P(t | T) = \frac{1}{T} \tag{2} $$ と書ける(ただし、$t \gt T$ に対しては $P(t|T)=0$)。
他方で、 $$ P(t) = \int_t^{\infty} P(t|T) \, P(T) \, dT = \frac{1}{L} \textrm{Ei}_1\left( \frac{t}{L}\right) \tag{3} $$ である。 ここで、積分で定義される関数を $$ \textrm{Ei}_1(x) = \int_1^\infty t^{-1} e^{-t x} dt $$ と置いた。
(1), (2), (3)式を使うと、ベイズの定理から $$ P(T | t) = \frac{P(t|T) \, P(T)}{P(t)} = \frac{1}{T} \exp\left( - \frac{T}{L} \right) \Big/ \textrm{Ei}_1\left( \frac{t}{L}\right) \tag{4} $$ を得る。
(4)式より、人類が $t$(万年)だけ生存していたことを知った上で、その$N$倍の$N t$ 万年までに絶滅する確率は $$ \sum_{T=t}^{T=N t} P(T|t) \approx \int_{t}^{N t} P(T|t) \, dT \tag{5} $$ と表現できる。
言うまでもなく、ここでの推定は、$L$の値に大きく依存する。
ここで、仮に、$L=100$万年として、 人類の誕生からの経過時間 $t = 20$万年を入れ $$ \int_{20}^{N \times 20} P(T|20) \, dT = 0.95 \tag{6} $$ を数値的に解くと、 $$ N \approx 9.2 $$ が得られる。
つまり、上記の見積もりが正しければ、95%の確率でこれまでの9倍程度の期間内に、すなわち $$ 20 \times 9.2 = 180 $$ 万年くらい先までには人類は絶滅するであろう、という結果が得られた。
SciPyの機能を使って、(6)式の根を数値的に求めるコードの例。
# coding: utf-8
import math
import numpy as np
from scipy import optimize,integrate
def Li1(x):
val,err = integrate.quad(lambda t:1/t*math.exp(-t*x),1,np.inf)
return val
def G(x):
L=100
t=20
val,err = integrate.quad(lambda T:1/T*math.exp(-T/L), t,t*x)
return val/Li1(t/L) - 0.95
roots = optimize.fsolve(G,1)
print("Roots=",roots)
以上をまとめると、Python 3のdatetimeモジュールで表現できる年数(9999)は、未来の我々にとっては不十分と思われる。 一方、64ビットの整数で表現したUnix時間を使えば、人類滅亡までのカウントダウン(アップ?)は十分に可能と予想できる。
別の議論の例
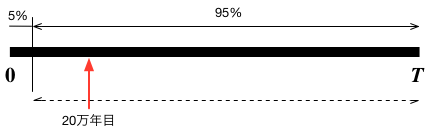
人類の存続期間$T$があらかじめ定められており、我々はその期間の中のどこかの時点で等しい確率で生を受けたとする。 $T$全体を、最初の5%の区間と、残りの95%の区間に分けると、我々は95%の確率で「後半」の区間に生存していることになる。 それが95%の区間の最初の時点、すなわち $t = T \times 0.05$(万年目)とすれば、人類はこれからさらに$t \times \frac{0.95}{0.05}$万年生存できることになる。 他方で、95%の区間の最後に位置する場合は、明日にでも人類は滅亡することになる。
ここで、$t$を人類誕生からの年数である20万年と置くと、 $$ 20 \times \frac{0.95}{0.05} = 20 \times 19 = 380 \tag{7} $$ 万年が、95%の確率で人類の(最大限の)持ち時間ということになる。
 解説: 原子の寿命と無記憶性
解説: 原子の寿命と無記憶性
時刻$t=0$に$n_0$個の不安定な原子核があったとすると、 崩壊によって別の核種に変化することで、その数は指数関数的に減少することが知られている。 例えば、核実験や原発で生成される放射性のセシウム137は、半減期が約30年である。 そうすると、ここにセシウム137の原子が$n_0$個あったとすると、それが$t$年後には $$ n(t) = n_0 \left(\frac{1}{2}\right)^{\frac{t}{30}} = n_0 \, e^{- \frac{\log 2}{30} t} \tag{8} $$ に減少することになる。
半減期を$T_h$として、$\tau = T_h/\log 2$と置くと、 それぞれの原子核が時間あたりに崩壊する確率は(経過年数には依らず)常に $1/\tau$ になる。 すなわち、$t$から$t + \Delta t$の間に、$n(t)$個の原子核のうちの$\delta/\tau$だけが崩壊して個数を減らすとすれば $$ n(t+\Delta t) = n(t) - \frac{\Delta t}{\tau} n(t) \tag{9} $$ となる。$\Delta t \to 0$で、これは微分方程式 $$ \frac{d n(t)}{dt} = - \frac{n(t)}{\tau} \tag{10} $$ に帰着でき、その解が (8)式に他ならない。
よく考えると、これは少なからず不思議な気がする。 というのは、原発などで生成されたばかりの「真新しい」放射性の原子と、崩壊しないまま長年残存していた原子核との間に全く違いはなく、 「長生き」した原子核のほうが崩壊しやすい、といった傾向は一切ない、と言っているからである。 言い換えれば、原子は自分の過去を全く覚えていない、ということになる(無記憶性)。
この様子をもう少し詳しく考えてみよう。
時間の原点をどこかに設け、原子の崩壊のようなイベント起こる時刻を$T$とする。 イベントが$t$以後に発生する確率を $P(T \gt t )$と書くことにする。
そして、$t$以降にイベントが発生したことを知った上で、$t$から起算して$s \; (\ge 0)$以降にイベントが発生する条件付き確率 $P(T \gt s + t | T \gt t)$ を考えると、条件付き確率の定義から、 $$ P(T \gt s + t | T \gt t) = \frac{P(T \gt s + t , T \gt t)}{P(T \gt t)} \tag{11} $$ となる。 ここで同時確率 $P(T \gt s + t , T \gt t)$ の意味するところ考えると、$t$以降にイベントが発生し、かつ、$t+s$以降にイベントが発生する確率は $$ P(T \gt s + t , T \gt t) = P(T \gt s + t) \tag{12} $$ であることは明らかである。よって (11)式は $$ P(T \gt s + t | T \gt t) = \frac{P(T \gt s + t)}{P(T \gt t)} \tag{13} $$ となる。
イベントが発生する確率密度が指数分布の場合、すなわち $$ p(t) \, dt = \tau e^{-\frac{t}{\tau}} \, dt \tag{14} $$ の場合、累積確率分布は $$ P(T \gt t) = \int_t^\infty p(t') dt' = e^{-\frac{t}{\tau}} \tag{15} $$ であるから、これを (13)式に代入すると $$ P(T \gt s + t | T \gt t) = \frac{\exp(-\frac{s+t}{\tau})}{\exp(-\frac{t}{\tau})} = e^{-\frac{s}{\tau}} = P(T \gt s) \tag{16} $$ となる。
すなわち、指数分布に従ってランダムに生じるイベントでは、条件付き確率は$t$に関係せず、「これから先」のことは「これまで」と全く無関係に起こる。
逆に、無記憶性の条件 $$ P(T \gt s + t | T \gt t) = \frac{P(T \gt s+t)}{P(T \gt t)} = P(T \gt s) $$ から出発して、$ f(t) = P(T \gt t)$と表記し直すと、 関数方程式 $$ f(s+t) = f(t) \, f(s) $$ が得られるが、$f(t)$の連続性を仮定すると、その解は指数関数 $f(t) = a \exp(-b t)$ となる。
 練習:バスの待ち時間
練習:バスの待ち時間
あるバス停では、バスが到着するまでの時間間隔が指数分布に従っていることが分かっている(平均間隔は10分とする)。 あなたがバス停に来た時点ですでに人が並んでいたので、列の先頭の人に尋ねると、「5分間そこで待っている」と教えてもらった。
あなたはそのバス停で平均あと何分待たなければならないか、考えてみなさい。