ブートストラップ法

このページでは、ブートストラップ法による母数の推定を試してみる。

平均値の信頼区間

母平均 $\mu$、母分散 $\sigma^2$ の母集団から $N$ 個のデータ $x_1, x_2 \cdots x_N$ を取得したとき、サンプルの平均 $$ \bar{x} = \frac{1}{N} \sum_{i=1}^N x_i $$ および不偏分散 $$ U = \frac{1}{N-1} \sum_{i=1}^M (x_i - \bar{x})^2 $$ は、いずれも

1. $N$を大きくすれば、どんどん母数に近づいていく（一致性）
2. 小さい$N$のサンプルからの推定値でも、それを何度も繰り返して平均すると、母数に近づく（不偏性）

という性質があった。

一方、中心極限定理から、サンプル平均 $\bar{x}$は正規分布に従う $$ \bar{x} \sim N(\mu, \sigma^2/N) $$ ことがわかっている。 もし母分散が既知であれば（そういう場合は少ないであろうが）、下図のように、サンプル平均が正規分布の「両端」にあるような状況の「あいだ」に、母平均は位置しているはずである：

すると、母平均の 95%の信頼区間（両端 2.5%ずつを除く区間）として、よく使われる式 $$ \bar{x} - 1.96 \, \sigma/\sqrt{N} \le \mu \le \bar{x} + 1.96 \, \sigma/\sqrt{N} $$ が得られる。

母分散が未知の場合は、分散の推定値として不偏分散 $U$ を用いることになるが、$U$ は確率変数として扱わなければならないので、t検定量 $$ t = \frac{\bar{x} - \mu}{\sqrt{U \big/ N}} $$ を使っての議論となる（詳細は省略）。

このように、母平均のみを考えるのであれば、中心極限定理によってサンプル平均の正規性が保証されているので、信頼区間の推定はさして困難ではない。

ところが、その他の母数を推定したい場合、サンプル値の分布がどのようであるべきか、見当がつかないことが多く、信頼区間の推定も困難となる。

サンプルを母集団の「コピー」と思ってサンプリングする

母集団から得た $N$ 個のサンプルが、偏りなくランダムに選ばれているなら、そのサンプル自体も母集団の分布を反映していると考えるのは自然であろう。 例えば、母集団全体で 1000000 人の対象者がいて、標本は100人分であったとすると、100人分の標本を10000回複製して作成したデータの統計的性質は、母集団のそれに近いはずである。

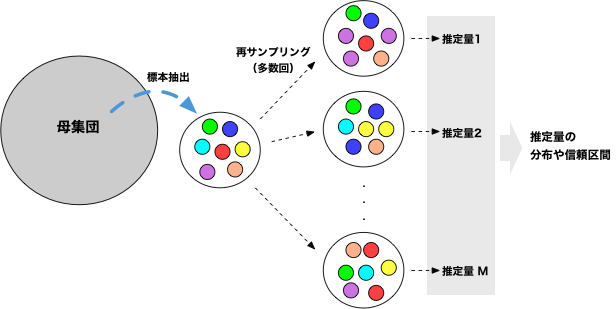
そうやって水増ししたデータを作成してから標本を得る代わりに、100人分のサンプルから、重複を許しながらサンプルし直しても同じことである。 このように、標本を元にサンプルを取り直し、それを元に推定値の分布や信頼区間を議論する方法をブートストラップ法(bootstrap method)と呼ぶ。 Bootstrapという語は「少ない資源をうまくやりくりして、次の段階に繋げる」といったニュアンスで使われるので、少数のサンプルから母数を推定する、といったイメージで用いられるようになったのだろう。

その手順自体はシンプルである：

1. サンプルを得る $x_1, x_2, \cdots, x_N$
2. 以下を$M$回繰り返す：
3. 　サンプルから重複を許しながら$N$個のデータをサンプルし直す（$y_1, \cdots, y_N$とする)。
4. 　取り直したサンプルを使って推定したい量を求める $\theta_k = G(\{y_i\})$
5. $\{ \theta_k \}$の平均を母数の推定値とし、その分布から分散や信頼区間を推定する。

Weibull分布の母数の推定

時間間隔 $\tau$ が Weibull分布 $$ p(\tau) = \frac{\alpha}{\beta^\alpha} \tau^{\alpha-1} \exp\left( -\left( \tau \big/ \beta \right)^\alpha \right) $$ に従うような事象からのサンプルを考えてみよう。得られるのは、事象ごとの時間間隔 $\tau_i$ である。 このデータから母数 $\alpha, \, \beta$を見積もる方法について考えてみたい。

累積分布を計算すると $$ P(\tau) = \int_0^\tau p(\tau) \, d\tau = 1 - \exp\left( -\left( \tau \big/ \beta \right)^\alpha \right) $$ となるから、式を変形して、二回対数を取ることで $$ \log\left( -\log\left(1-P(\tau) \right)\right) = \alpha \log \tau - \alpha \log \beta $$ が得られる。

つまり、データから累積頻度を求め、 $$ Y_i = \log\left( -\log\left(1-P(\tau_i) \right)\right) $$ $$ X_i = \log \tau_i $$ とおけば、 $$ Y_i = \alpha \, X_i - \alpha \log \beta $$ の傾きと切片から $\alpha$, $\beta$ の推定値が得られるはずである。傾きと切片の推定には最小二乗法を使えばよい。

実際に得られたサンプルを小さい順に並べ替えたデータを $\tau_1, \tau_2, \cdots, \tau_N$ とすれば、データの累積密度は $$ P(\tau_i) = \frac{i}{N+1} $$ を通る階段状になる。

上記の手順に沿って、リストsample中のデータを nb回 サンプリングし直し、母数の推定値とその標準偏差を求めるコードの例を以下に示す。

# coding: utf-8

import math
import numpy as np

samples=[3,2,4,2,2,1,4,2,10,4,3,4,4,3,3,9,9,3,4,3,9,4,5,9,7,7,3,7]
nsample=len(samples)

nb=1000
alphas=[]
betas=[]
P = np.ones((nsample,)).cumsum()/(nsample+1)
Y =np.log(- np.log(1-P))
for _ in range(nb):
    taus = np.sort( np.random.choice(samples,size=nsample,replace=True) )
    X = np.log(taus)
    a,b = np.polyfit(X,Y,1)
    alphas.append(a)
    betas.append(math.exp(-b/a))

alphas = np.array(alphas)
mua=alphas.mean()
s2=0
for i in range(nb):
    s2 += (alphas[i] - mua)**2
sea=math.sqrt(s2/(nb-1))
print('alpha:',mua,sea)

betas = np.array(betas)
mub=betas.mean()
s2=0
for i in range(nb):
    s2 += (betas[i] - mub)**2
seb=math.sqrt(s2/(nb-1))
print('beta:',mub,seb)

　練習：母数の推定

上記の例に倣って、指数分布 $$ p(\tau) = \frac{1}{\lambda} \exp(-\tau/\lambda) $$ に従って生成したサンプルから、母数 $\lambda$ を推定するコードを作成してみなさい。

サンプルを生成する部分は、SciPyを使って、以下のように書けばよい：

import math
from scipy.stats import expon
import numpy as np

lambd=2.0
nsample = 30
samples = expon.rvs(scale=lambd, size=nsample)