線形計画問題の双対性

このページでは線形計画問題の双対性について、「円による縄張り」問題を例に考える。

目的関数の最大値を見積もる（３つの円の場合）

別ページで述べた円による縄張り問題で、 目的関数（半径の和）が最大でどれくらいまで大きくすることができるものか、 異なるアプローチで考えてみたい。 一般的に考えるのは難しそうなので、点（円）が３つの例について考えてみよう。 この場合、線形計画問題の制約条件は $$ r_1 + r_2 \le 1 \\ r_2 + r_3 \le \sqrt{5} \\ r_1 + r_3 \le 2 \\ r_1 \ge 0 \\ r_2 \ge 0 \\ r_3 \ge 0 $$ で、最大化したい目的関数は $$ z = r_1 + r_2 + r_3 $$ であった。

ここで、天下り的ではあるが、新しい変数 $y_{12}, y_{23}, y_{13} (\ge 0)$を導入して、 $$ G = (r_1 + r_2) y_{12} + (r_2 + r_3) y_{23} + (r_1 + r_3) y_{13} $$ の値を評価してみよう。ここで、$y_{ij}$についての「係数」にあたる部分は、元々の問題の制約条件の左辺のパターンになっており、 それぞれ $r_1 + r_2 \le 1, r_2 + r_3 \le \sqrt{5}, r_1 + r_3 \le 2$ の制約が課せられているわけだから、明らかに $$ G \le 1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13} $$ である。

一方で、$G$を$r_i$について整理すると $$ G = (y_{12} + y_{13}) \, r_1 + (y_{12} + y_{23}) \, r_2 + (y_{23} + y_{13}) \, r_3 $$ となる。 ここで、仮に、$r_i$の「係数」部分が$y_{12}+y_{13}=1, y_{12}+y_{23}=1, y_{23}+y_{13}=1$となるような$y_{ij}$の組が存在したなら、 $G$ は目的関数 $z$ に一致するので、目的関数 $z$ の最大値は、$G$ の最大値に他ならない。 そして、上でみたとおり、$1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13}$ が $G$ の上限を与えている。

ただし、一般の問題で、$z=G$となるような丁度良い$y$の組が唯一に決まるかどうかは保証の限りでない（下で述べるように、変数の数よりも条件のほうが少ない可能性がある）。 そこで、「汎用的」なアプローチとして、$z \le G$ すなわち $$ r_1 + r_2 + r_3 \le (y_{12} + y_{13}) \, r_1 + (y_{12} + y_{23}) \, r_2 + (y_{23} + y_{13}) \, r_3 $$ という制約を満たすような $y_{ij}$ の中から $G$ の上限が一番小さくなる組み合わせを見つけ出す（$z$の値を上から押さえる）という方略を採ることにする。 ここで $r_i, y_{ij} \ge 0$であるから、 $z \le G$ という制約は、 $$ 1 \le y_{12} + y_{13} \\ 1 \le y_{12} + y_{23} \\ 1 \le y_{23} + y_{13} $$ と整理することができる。 以上の議論で、この制約のもとで、 $$ 1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13} $$ を最小化できれば、それによって $z$ の値を上から押さえることができるはずだ。

改めて整理すると、$z$ の最大値を求める問題は、制約条件 $$ y_{12} + y_{13} \ge 1 \\ y_{12} + y_{23} \ge 1 \\ y_{23} + y_{13} \ge 1 \\ y_{12} \ge 0 \\ y_{23} \ge 0 \\ y_{13} \ge 0 $$ のもとで、 $$ w = 1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13} $$ を最小化する線形計画問題と見なすことができる。 この問題は、元々の問題($z$の最大化）と双対(dual)な関係にある、と言う。

円による縄張り問題の最適解

上の説明で、3つの円による「縄張り問題」については、$G$ と $z$ が完全に一致する条件 $$ y_{12} + y_{13} = 1\\ y_{12} + y_{23} = 1\\ y_{13} + y_{23} = 1 $$ を満たす（ほとんど自明な）解が存在して、 $$ y_{12} = y_{23} = y_{13} = 1/2 $$ であり、 このとき $G$ の上限は $$ z = G \le 1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13} = \frac{1+\sqrt{5}+2}{2} $$ と評価できる。 そして、この右辺は、うまい具合に、$z$ の最大値と一致している （このことは自明ではないが、$z$の最大値と$w$の最小値は一致することが証明できる）。

4点以上の場合になると、変数 $y_{ij}$ は6つ現れるのに対して(4点から2点を選ぶ組み合わせの数）、条件式は4つ（点の数）なので、連立方程式を立てても、解は一意に定まらない。 つまり、単体法などを使い、線形計画問題として解く必要が出てくる。

問題の再解釈

では、上記の議論で登場した $y_{ij}$ とは、一体何を表しているのだろうか。

双対な問題のほうの目的関数 $$ w = 1 y_{12} + \sqrt{5} \, y_{23} + 2 y_{13} $$ を眺めると、$1, \sqrt{5}, 2$ は点同士の距離であったから、この式は距離に $y_{ij}$ で重みをつけて加えた形になっている。 つまり、$y_{ij}$は、点と点の間の隙間が、目的関数全体にとってどれくらい貢献しているか、を表している。

一方で、新しい制約条件（で最適値が達成されているような場合）、例えば $$ y_{12} + y_{13} = 1 $$ は、 点1と点2、および点1と点3の間の空隙の「貢献度」の配分の程度を決めている。 仮に $y_{12}=1, y_{13}=0$ ならば、1と3の空隙は目的関数への寄与が無いことを表す。

半径 $r$ を変数とした元々の問題設定では、それぞれの円に着目していたものを、双対な問題では、互いの接触の様子が変量となるように、見方を変えたわけである。

感じをつかむために、以下の「6つの点」のケースについて、もう少し考えてみたい。赤で示した点は、中央のやや大きめの点の周りに、それを中心として正五角形を成すように配されている。 また、この場合の縄張り問題の最適解（のイメージ図）も描いておいた。

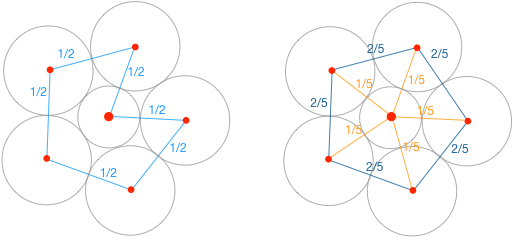
記号 $\sum_{j (\ne i)}$ は、$j$についての総和（ただし$j \ne i$ の場合について）。

図には、ある点$i$に着目した際に、ちょうど $\sum_{j (\ne i)} y_{ij} = 1$ となるような $y_{ij}$ の割り付けの例が書き添えてある。 ただし、図で、値が0のリンクは省略してある。

例えば、左側の図では、各点から、値1/2のリンクが2本ずつ出ているので、点ごとに、その総和は 1/2 + 1/2 = 1 となる。 右図は、別の可能性だが、やはり、各点毎の総和は1になることが確認できるだろう（中心の点は 1/5+1/5+1/5+1/5+1/5=1。その他は、1/5 + 2/5 + 2/5 = 1。） リンクで結ばれたところは、丁度円が接しており、その距離を $d_{ij}$ とすれば、全体的な円の半径の和に対するその部分の寄与は「無駄無く」 $y_{ij} d_{ij}$ となる。そして、この場合、どちらで計算しても目的関数は同じ値（最小値）となる。ここで、「総和が1」という条件は、各円からの寄与のダブルカウントを避けるために必要である。

双対な問題の一般的な構成方法

円による縄張り問題で、双対な問題を生成した手続きをさらに一般化し、 以下のようにまとめることができる：

変数 ${\bf x} = (x_1, x_2, \cdots, x_n)^\textrm{T}$についての線形計画問題の制約条件が、行列 $A$ ($m$行$n$列）を使って $$ A {\bf x} \le {\bf b} \\ {\bf x} \ge 0 $$ 最大化すべき目的関数が $$ z = {\bf c}^\textrm{T} \, {\bf x} $$ で与えられるとき、それに双対な問題は、制約条件が $$ A^\textrm{T} {\bf y} \ge {\bf c} \\ {\bf y} \ge 0 $$ 最小化すべき目的関数が $$ w ={\bf b }^\textrm{T} \, {\bf y} $$ で与えられる。 双対な問題では、行列が転置され、目的関数の最大化は最小化に転じ、制約条件の不等号の向きが逆になる。

そして、元々の問題に最大値が存在する場合、それは双対問題の最小値と一致することが証明されている。 その辺りの詳細は、線形計画法の専門書などにあたること。