線形計画法による最適化
このページでは、グラフィック描画に線形計画法を応用する例を紹介する。
円で「効率的に」空間を仕切る方法
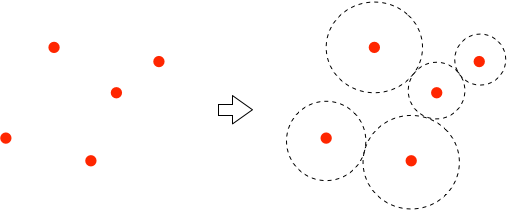
二次元平面に$n$個の点があって、それぞれの座標が$(x_i, y_i)$ (ただし、$i=1,2,\cdots,n$)であったとしよう。 そして、各点を中心として、半径$r_i$の円を描く。 すると、$n$個の円が描かれることになるわけだが、ここで、以下の条件(制約)を課すことにしよう:
- 円は互いに重なりあってはならない
- 円が他の円の内側に含まれてもいけない
- 半径は必ず正の値を取る
円の面積の合計 $$ \sum_i^n \pi {r_i}^2 $$ の最大化も考えられるが、こちらは非線形な問題となって、ちょっと手強くなる。
これらの制約の下で、円の周長の合計すなわち $$ \sum_i^n 2 \pi r_i $$ を目的関数として、これを最大にするような $r_i$ の組み合わせを求める方法について考えよう。 つまり、円によって空間をできるだけ「効率的に」仕切ることのできるような半径の組み合わせを問題にするわけである。 あるいは、「円による縄張り問題」と言って良いかもしれない。 ただし、上の目的関数は、 $$ z = \sum_i^n r_i $$ を最大化する、と言い換えても全く同じことなので、以下ではこの$z$の最大化について考えることにしよう。
点の配置が与えられたとき、それを中心とした互いに重ならない円を描いて、効率よく空間を埋めるためには、それぞれの円の半径をどのように選んだら良いだろう?
複数の箇所から増殖する微生物のコロニーや植物のニッチが、どのように空間的に広がるかを抽象化すると、これと似た捉え方が可能かもしれない。
また、炭酸飲料の入った瓶やグラスの内側に発生する泡のサイズも、類似の問題のように思われる。
線形計画問題として考える
以下の説明は、参考書 3.7節(p.89)と併せて読むとよい。
また、線形計画問題についての補足をこちらのページに記した。
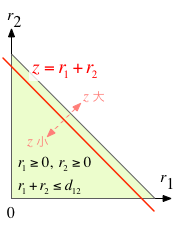
二つの円による縄張り問題。薄緑色で示す制約条件の領域に赤色の直線が「触れている」範囲で、$z$を最大化する。
座標が$(x_1, y_1)$の点1と、$(x_2, y_2)$の点2の間の距離を$d_{12}$表記することにしよう (これを $d_{21}$ と書いても同じことだが、以下では添字が小さい順に並ぶほうを用いることにする)。 その具体的な値は、 $$ d_{12} = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} $$ である。
このとき、$z$を最大化するのは、明らかに、$r_1 + r_2 = d_{12}$、すなわち2つの円が接しているときである。 ところが、$r_1 + r_2$ は目的関数 $z$ に他ならないので、この場合は、2つの円が接してさえいれば、周長の和も最大となる。 つまり、$z$を最大にする半径の組み合わせは無数にあって、唯一に定まらないものの、 $z$ が最大化された状態では、『なるべく円が互いにちょうど接するようになっている』ことが期待される。
点が沢山ある場合はとても複雑そうに感じられるが、 考慮しなければならない条件の表式は案外と単純で、円同士が重ならないための条件 $$ r_i + r_j \le d_{ij} $$ (ただし、$i\neq j$)、および半径の非負性 $$ r_i \ge 0 $$ のみである。
この問題は、$r_i$についての線形な不等式によって制約条件が記述され、 $r_i$について線形な目的関数の最大化がゴールであるから、参考書 p.89 で述べられている線形計画問題として 扱うことができるはずだ。
では、3つの点(点1: $(0,0)$, 点2: $(1,0)$, 点3: $(0,2)$)の場合について、制約条件と目的関数がどうなるか、考えてみよう。 それぞれの点の間の距離は $$ d_{12}=1, \;\; d_{13}=2, \;\; d_{23}=\sqrt{5} $$ である。 点の位置関係と、「縄張り円」のイメージ図を以下に示す:
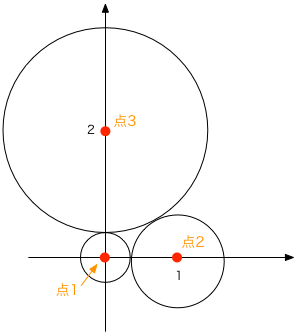
これを、参考書の問題3.36(p.96)に倣った形式で書くと、制約条件 $$ r_1 + r_2 \le 1 \\ r_2 + r_3 \le \sqrt{5} \\ r_1 + r_3 \le 2 \\ r_1 \ge 0 \\ r_2 \ge 0 \\ r_3 \ge 0 $$ のもとで、目的関数 $$ r_1 + r_2 + r_3 $$ を最大にするような$r_1, r_2, r_3$の組を求めればよい、ということになる (参考書の$x_i$を$r_i$と読み替えれば、対応は明らかであろう)。
単体法に基づくPythonのプログラムを使って、線形計画問題を解く
アルゴリズム13, 14を用いる際の条件については、参考書を参照のこと。
では、上記の「3点問題」をコンピュータに解かせてみよう。
参考書で紹介されている単体法(線形計画法を解くアルゴリズム:Algorithm 13および14)を、できるだけ素直にPythonのコードに 翻訳したプログラムを用意しておいた:
準備として、上のリンクを右クリックして、ファイル simplex.py を作業用のディレクトリにダウンロード・保存しておく。
次に、simplex.pyと同じディレクトリに、以下のPythonコードを作成・保存する:
# coding: utf-8
from simplex import SimplexMethod
import math
# 問題のサイズに応じて、NとMの値を変更する
N=3
M=3
q = SimplexMethod(N,M)
# 制約条件を表現する係数行列
a =[
[1,1,0],
[0,1,1],
[1,0,1]
]
# b の値
b = [1,math.sqrt(5),2]
# z の式の係数
c = [1,1,1]
q.init_coef(a, b, c)
res = q.simplex()
if res>0:
q.print_solution()
このコードを実行すると、
x[0]= 0.3819660112501051 x[1]= 0.6180339887498949 x[2]= 1.618033988749895 z= 2.618033988749895
が出力される。 Pythonではリストの添字が1からではなく0から始まることを反映して、上記の説明とは、添字が1だけずれている点に注意。 この出力結果は、問題の解が $r_1=0.381966, \; r_2=0.618034, \; r_2=1.618034$、 そして、目的関数の値が $z=2.618034$ であることを示している(ただし、いずれも数値的な近似値)。
問題のサイズや制約条件、目的関数を変えてみる
線形計画法を解くには、すでに様々なソフトウェアが開発されていて、そうしたソフトでは色々な「職人技」も施されており、 大規模な問題でも効率よく解を求めることができるようになっている。 例えば、一般的な表計算ソフト Microsoft Excel にも、線形計画法のための計算プログラム(ソルバー)が提供されている。
従って、問題の抽象化と条件式(パラメータ)の决定までは我々自身で行なう必要があっても、線形計画法のプログラムの コーディングまでは必要とされないケースが殆どかもしれない。
ここでは、上で示したサンプルコードに若干の手直しを施すことで、「円による縄張り問題」に限らず、さらに一般的な線形計画問題
右は参考書3.7節で述べられている「焙煎コーヒー」での仮定を若干緩めた表現になっている。

を解く際の手順とヒントを述べる。
変数と条件の数の設定
まず、単体法のプログラムが格納されているファイル simplex.py を 「取り込む」ために
from simplex import SimplexMethod
の1行を加える。
次いで、問題のサイズ(参考書 p.89から103にかけての説明の、変数の数$n$と条件の数$m$)を与えて、SimplexMethodのインスタンスを作成する:
N=3 M=3 q = SimplexMethod(N,M)
問題のサイズに応じて、$M$と$N$の値は調整する。
制約条件と目的関数
上記のサンプルプログラムで、参考書の式(3.48)の左辺の係数行列$a_{ij}$は、 二次元リストとして
配列の[ ]のバランスと、区切りのコンマを忘れぬように注意。
a =[
[1,1,0],
[0,1,1],
[1,0,1]
]
で、右辺の$b_i$は、
b = [1,sqrt(5),2]
で設定されている。 Pythonコードと係数の対応関係を、念のため、以下に示しておく:
参考書の説明とPythonプログラムとは、添字の対応関係が1だけずれていることに注意。
例えば、参考書での$b_1$は、Pythonコードではb[0]に対応。

一方、参考書 (3.49)式の制約条件($r_i \ge 0$)は、プログラムでは設定する必要はない。
また、目的関数(参考書 式(3.50), $z = \sum_i^n c_i r_i$) の係数 $c_i$ は
c = [1,1,1]
となっている。これは、もちろん、$z=1 r_1 + 1 r_2 + 1 r_3$を意味している。
標準形への変換と、単体法による計算
配列に格納された条件を元に、参考書の式(3.51)-(3.53)の標準形を生成し、計算の準備を行なっているのが
q.init_coef(a, b, c)
次いで、単体法で最適解を計算するのが
res = q.simplex()
である。メソッドsimplex()は、最適解が見つかった場合は1を、
そうでない場合(参考書 p.103のAlgorithm 14で"unbounded"が出力される場合)は-1を、戻り値として返す仕様になっている。
この場合、int型の変数resに、計算がうまく行ったかどうかが格納される。
計算結果の取得
メソッドのまとめ:
init_coef(a,b,c)
リスト(配列)a,b,cに基いて計算の準備を行う。
simplex()
単体法で問題を解く。
解が見つからなかった場合は戻り値が-1。
print_solution()
計算結果のまとめを表示する。
get_opt_param(i)
最適条件でのi番目(0番目から始まる)の変数の値を返す。
get_opt_value()
最適値(最大値)の値を返す。
計算の結果は、画面に表示したり、数式中でその値を用いたりすることができる。
上記のサンプルプログラムでは
print_solution
メソッドを呼び出して計算結果の一覧を画面に表示している。
表示だけでなく、線形計画問題を解いて得られた値(最適条件での変数の値)を使ってさらに処理を進める場合には get_opt_param() メソッドを用いる。
例えば、目的関数が最大となったときの3番目の変数の値を、変数 x2 に代入する操作は、
x2 = q.get_opt_param(2)
となる。ここで、引数は「何番目の変数か」を表しており、、Pythonのルールに倣って、0番目から始める。 であるから、2 は「3番目」の変数を意味する(一方、参考書の説明では、添字は1から始まる)。
このget_opt_param()メソッドを使うと、(print_solution()を使わずとも)
q.init_coef(a, b, c) ;
res = q.simplex() ;
if res>0:
for i in range(N):
print("r[",i,"]= ",q.get_opt_param())
print("z= ",q.get_opt_value())
のように結果を表示できる。ここで、get_opt_value()は、計算で得られた目的関数 $z$ の最大値を返すメソッドである。