Pythonプログラミング（ステップ７・F分布）

このページでは、等分散性検定を行う際に必要となるF統計量とその分布関数について述べる。

不偏分散の確率分布

平均0、分散1の正規分布に従う互いに独立な$n$個の確率変数$X_1, X_2, \cdots, X_n$を考える。 平均を $$ \bar{X} = \frac{1}{n} \sum_i^n X_i \tag{1} $$ として、平均との差の二乗和 $$ Z = \sum_i^n \left( X_i - \bar{X} \right)^2 = \sum_i^n {X_i}^2 - 2 \bar{X} \sum_i^n X_i + {\bar{X}}^2 \sum_i^n 1 = \sum_i^n {X_i}^2 - n {\bar{X}}^2 \tag{2} $$ はどのような確率分布に従うだろうか。

ここで、 $$ \boldsymbol{X} = \left( \begin{array}{c} X_1\\ X_2\\ \vdots\\ X_n \end{array} \right) $$ を$n$次元ベクトルと考えれば、 上の式の$\sum_i^n {X_i}^2$はベクトルの長さの二乗に他ならない。 そこで、ある回転行列$Q$を考えて、$\boldsymbol{X}$を $$ \boldsymbol{Y} = Q \boldsymbol{X} $$ と座標変換してみる。回転してもベクトルの長さは変わらないので、$Q$には依らず $$ \sum_i^n {Y_i}^2 = \sum_i^n {X_i}^2 $$ が成り立つ。

ここで、回転のしかたは任意なので、$Q$の成分を $$ Y_n = \frac{1}{\sqrt{n}} (X_1 + X_2 + \cdots + X_n) $$ のように選ぶことが可能である($Q$の$n$行目の要素を$q_{n,i}=1/\sqrt{n}$と設定する)。 すると、 $$ \begin{eqnarray} Z = \sum_i^n {X_i}^2 - n {\bar{X}}^2 = \sum_i^n {Y_i}^2 - n {\bar{X}}^2 \\ = \sum_i^n {Y_i}^2 - {Y_n}^2 = \sum_i^{n-1} {Y_i}^2 \end{eqnarray} \tag{3} $$ となって、$Z$は $Y$ の $n-1$ 個の二乗和で表されることがわかる。

一方で、$Q$の$i$行$j$列の要素を$q_{i,j}$と表すことにすると、 $$ Y_i = \sum_j^n q_{i,j} X_j $$ であるから、$X_j$は平均0、分散1と仮定していたことを思い出すと、 $$ Y_i \sim N(0, \sum_{j}^n {q_{i,j}}^2) $$ となるが、回転行列の性質から $\sum_{j}^n {q_{i,j}}^2=1$ であるので、結局、 回転後の変数も平均0、分散1 $$ Y_i \sim N(0,1) \tag{4} $$ のままとなる。

このように、(3)および(4)から、式(2)で定義された確率変数$Z$は、自由度$n-1$のカイ二乗分布に従うことがわかった。

以上から、$X_i$を母平均0、母分散1の母集団からのサンプルと見なせば、$n$個のサンプルについての不偏分散 $$ U_X = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2 $$ は、自由度$n-1$のカイ二乗統計量を$n-1$で割ったもの、とみなすことができる。

F統計量

２つの母集団XとYがあって、母分散は共に$\sigma^2$であったとする。 $X$から$n$個のサンプル $x_1, x_2, \cdots, x_n$、 $Y$からは$m$個のサンプル $y_1, y_2, \cdots, y_m$、がそれぞれ得られたとしよう。 そして、帰無仮説として『XとYの分散は等しい』を統計的に検定する方法について考える。

これらのデータについて、サンプル平均を $$ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i, \;\; \bar{y} = \frac{1}{m} \sum_{i=1}^m y_i $$ とすると、不偏分散はそれぞれ $$ U_X = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2 $$ $$ U_Y = \frac{1}{m-1} \sum_{i=1}^m (y_i - \bar{y})^2 $$ となる。

もしXのサンプルから得られた不偏分散$U_X$と、Yのそれ$U_Y$の比（F統計量と呼ばれる） $$ F = \frac{U_X}{U_Y} $$ が1に近ければ、２つの分散は「近い」と言えるだろう。しかしながら、$U_X$と$U_Y$は共にサンプリングの都度、確率的に変動するため、 仮に母分散が等しい場合であっても、上記の$F$は1の周りで変動する。 そのときの$F$の確率分布がわかっていれば、その変動幅がどの程度の確率で生じたものかを評価することができる。

ここで、分子と分母を共に$\sigma^2$で割って、 $$ F = \frac{\frac{1}{n-1} \sum_{i=1}^n \left(\frac{x_i - \bar{x}}{\sigma}\right)^2} {\frac{1}{m-1} \sum_{i=1}^m \left(\frac{y_i - \bar{y}}{\sigma}\right)^2} $$ を考えると、分子は自由度$n-1$のカイ二乗統計量を$n-1$で割った量、 分母も同様に自由度$m-1$のカイ二乗統計量を$m-1$で割った量となっており、それぞれは独立である。 このように、F統計量は、母集団の分散の絶対値に影響されないようにうまく定義されていることがわかる（$\sigma$が分子と分母でキャンセルするから）。

このように、$F$の確率分布は、２つの独立なカイ二乗分布に従う確率変数の比によって与えられることがわかった。

F分布関数

では、$F$は具体的にどのような確率密度に従うのであろうか。 こちらのページで説明したとおり、独立な確率変数$X$,$Y$から「合成」 された確率変数$Z=X/Y$の確率密度は $$ \begin{eqnarray} f_Z(z) & = & \int \int \, \delta(z - x/y) \,f_X(x) \, f_Y(y) \, dx dy \\ & = & \int \, f_X(yz) \, f_Y(y) \, |y| \, dy \end{eqnarray} $$ となる。これを、F分布の場合に当てはめてみる。

$X$は自由度$n-1$のカイ二乗分布に従う変数を$n-1$で割った量なので、 自由度$n-1$のカイ二乗分布の確率密度を$f(s;n-1)$とすると、$x = \frac{s}{n-1}$と変数を置き換え、 $$ f(x) \, dx = f( (n-1) s ; n-1 )\; (n-1) \, ds $$ となる。 このことを使うと、$X$の確率密度は $$ f_X(s) = \frac{ {((n-1) s)}^{(n-1)/2-1} e^{-(n-1)s/2}}{2^{(n-1)/2} \Gamma((n-1)/2)} (n-1) $$ 同様に、$Y$は $$ f_Y(t) = \frac{ {((m-1) t)}^{(m-1)/2-1} e^{-(m-1)t/2}}{2^{(m-1)/2} \Gamma((m-1)/2)} (m-1) $$ となる。

これらを使って、$X/Y$の密度関数は $$ \begin{eqnarray} f_Z(z) & = & (n-1)(m-1)\int_0^\infty \, \frac{((n-1) tz)^{(n-1)/2-1} e^{-((n-1)tz)/2}}{2^{(n-1)/2} \Gamma((n-1)/2)} \, \frac{((m-1)t)^{(m-1)/2-1} e^{-(m-1)t/2}}{2^{(m-1)/2} \Gamma((m-1)/2)} t \, dy \\ & = & \frac{ (n-1)^{(n-1)/2} (m-1)^{(m-1)/2} z^{(n-3)/2}}{2^{(n+m)/2-1}\Gamma((n-1)/2) \Gamma((m-1)/2)} \int_0^\infty t^{(n+m)/2-2} e^{-((n-1)tz)/2 - (m-1)t/2} dt \end{eqnarray} $$ ここで、積分のところは、変数変換してガンマ関数の定義をうまく当てはめると、 $$ \int_0^\infty t^{(n+m)/2-2} e^{-((n-1)tz)/2 - (m-1)y/2} dt = 2^{(n+m)/2-1} \, \Gamma((n+m)/2 -1) \, \left( m-1 + (n-1) z\right)^{-(n+m)/2+1} $$ となるので、これを代入すると、自由度が $n-1$, および $m-1$ の場合のF統計量の確率密度 $$ \begin{eqnarray} f_Z(z; n-1, m-1) & = & \frac{(n-1)^{(n-1)/2} (m-1)^{(m-1)/2}}{B\left((n-1)/2, (m-1)/2\right)} \frac{z^{(n-1)/2 -1 }} { \left( m-1 + (n-1) z\right)^{(n+m)/2-1}} \\ & = & \frac{(m-1)^{(m-1)/2} (n-1)^{(n-1)/2}}{B\left((n-1)/2, (m-1)/2\right)} \frac{z^{(n-1)/2} z^{-1}} { \left( m-1 + (n-1) z\right)^{(n+m)/2-1}} \end{eqnarray} $$ を得る。

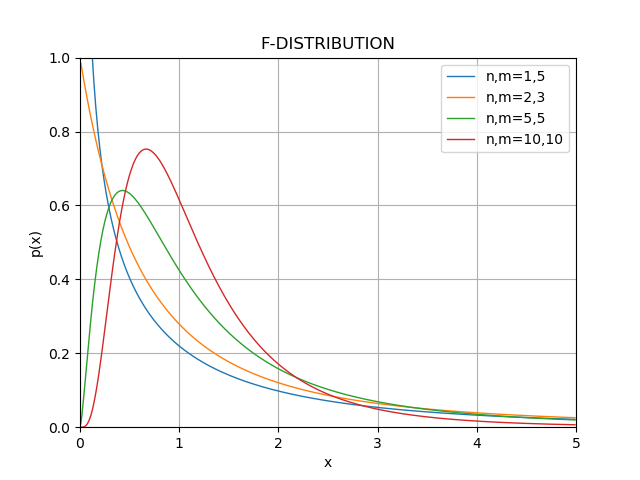
自由度 $n,m$ のF分布 $$ f_Z(z;n,m)=\frac{m^{m/2} n^{n/2}}{B\left(n/2, m/2\right)} \frac{z^{n/2} z^{-1}} { \left( m + n z\right)^{(n+m)/2}} $$ の様子を数通の自由度についてプロットするコードと出力の例を以下に示す：

# coding: utf-8

import math
import random
import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt

df = [[1,5],[2,3],[5,5],[10,10]]

xaxis = np.arange(0, 5, 0.01)

for x in df:
    n = x[0]
    m = x[1]
    fpdf = f.pdf(xaxis,n,m)
    plt.plot(xaxis,fpdf,'-', linewidth=1.0, label="n,m="+str(n)+","+str(m))

plt.title("F-DISTRIBUTION")
plt.xlim(0,5)
plt.ylim(0,1)
plt.legend()
plt.xlabel('x')
plt.ylabel('p(x)')
plt.grid(True)
plt.show()

　練習： 等分散の検定

以下のような２つのデータセット X, Y について、帰無仮説として『両者の分散は等しい』、対立仮説として『Yの分散が大きい』を設定の上、有意水準 0.05 で検定しなさい。

X: 30.069, 31.402, 30.545, 30.392, 31.849, 28.565, 30.002, 29.755


Y: 32.097, 30.546, 30.23, 35.453, 28.299, 31.463, 29.748, 32.249, 33.949

　ヒント