Pythonプログラミング（ステップ７・乱数と中心極限定理）

このページでは、確率や統計の分野で極めて重要な中心極限定理について考える。

1. 擬似乱数

コンピュータを使って、サイコロ投げなどのランダムな事象を模倣する際に、乱数を自動発生させる機能があると便利だ。 さもないと、「人間がサイコロを振って、出た目を、パソコンに入力する」といった作業を強いられることになる。 そのため、Pythonには乱数を発生させるための関数が用意されている。

使い方は、まず宣言部に

import random

と書いてから、random.randint(n,m) と呼ぶと、nからm（m自身を含む）までの間の整数が 等しい確率で、ランダムに返される。つまり、呼び出す度に、値が変わる。

また、random.random() と呼ぶと、0から1の範囲（1は含まない）のランダムな実数が返される。

擬似乱数を使って、「サイコロ」を10万回振り、出た目（リストの添字との対応がつけやすいので、サイコロの目は0から5まで、と考えた）の数と割合を出力するプログラム例を以下に示す：

# coding: utf-8
import random

dice=[0,0,0,0,0,0]

for cnt in range(0,100000,1):
    i = random.randint(0,5)
    dice[i] = dice[i] + 1

for i in range(0,6,1):
    print("サイコロの目:",i," 回数:",dice[i]," 確率:",dice[i]/cnt)

実数値の乱数

物理シミュレーション等では、特定の範囲の実数の乱数が必要になる場合が多い。aからbまでの範囲の実数乱数を得るには、0から1までの一様乱数を使って

x = a + random.random() * (b-a)

のように記述しても良いし、

x = random.uniform(a,b)

でもよい。ただし、前者は上端bを含まないのに対して、後者はbを含む点で違いがある。

　練習：モンテカルロ法

以下の考え方に基づいて、シミュレーションによって円周率の値を推定するプログラムを作成してみなさい。

1: 「大きな」数 n を決める
2: カウンター c をリセットする
3: 5までをn回反復する:
4:	0から1の間で一様に分布する二つの乱数 x, y を生成する
5:	もし x*x + y*y が1より小さければ（(x,y)が半径1の円の内部ならば）カウンター c を 1 だけ増やす
6: nが十分大きければ、この時点で、c/nは半径1の円の面積の1/4 (すなわちπ/4)になっているはずである。

　ヒント

サンプル数を$n$とすると、統計的な揺らぎは$1/\sqrt{n}$程度で減少するので、この種の計算では、誤差を1/10にするには、100倍の反復が必要となる。

2. 乱数の和

$X$を、サイコロの目など、ランダムに生じる数を表すとしよう。そして、同様の、しかし互いに独立な$n$回の試行の 1回目を$X_1$, 2回目を$X_2$, ... とし、それらの和を回数で割った量 $$ \bar{X}_n = \frac{X_1 + X_2 + \cdots + X_n}{n} $$ を考えると、大数の法則によって、$n \to \infty$で$\bar{X}_n$は$X$の平均値$\mu$に収束する。 1から6の目が同じ確率で出る（いかさまではない）サイコロの場合は、各目の出る確率は1/6なので、 $$ \bar{X}_n \to 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + \cdots + 6 \times \frac{1}{6} = 3.5 $$ となるわけだ。

では、次に、$n$で割らないで、単純に加えた数 $X_1 + X_2 + \cdots + X_n$ は$n$を大きくすると、どのように振る舞うであろうか。 サイコロの例を念頭に考えると、$n$を増やすとともに、その和もまた増大することは明らかであるが、それに加えて、総和した値の変動幅も大きくなるのではないだろうか？

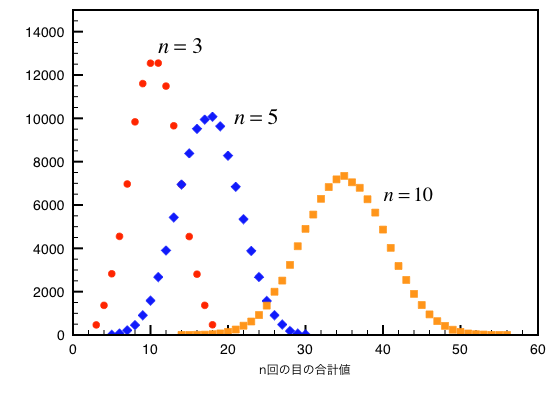
そこで、実際に、コンピュータ上でサイコロを振って、この様子を確かめてみた。 下のグラフは、『サイコロを$n$回振って、その目の合計を調べる』作業を10万回繰り返し、目の合計値がどのように分布するかをプロットしたものである。 ここで、$n$は、3, 5, 10の場合について調べた。

すると、よく見慣れたベル型の分布が現れるのが分かる。 この様子を数学的に表現したのが中心極限定理である。 すなわち、 $X_i$の平均を$\mu$、分散を$\sigma^2$とすると、それらの$n$項分の和の分布は、平均$n \mu$, 分散$n \sigma^2$の正規分布に漸近する。 すなわち、$n \gg 1$ で $$ X_1 + X_2 + \cdots + X_n \sim N(n \mu, n \sigma^2) $$ となる。 同じことではあるが、$n$個のサンプルの平均は、$n \gg 1$で $$ \frac{X_1 + X_2 + \cdots + X_n}{n} \sim N\left(\mu, \sigma^2/n\right) $$ となる、と表現することもできる。このとき、$X_i$の分布は（平均と分散が有限ならば）どんな形でも構わない。

上のグラフからも分かるように、元の $X_i$ は正規分布とは程遠い分布型にも関わらず、$n$が5程度でも、その総和は正規分布に近い形になっている点に注目したい。 このことはまた、少数であっても、何らかのランダムな要因が加算的に作用すると、その結果として、正規分布が現れる可能性を示唆しており、正規分布が様々な現象に顔を出すひとつの理由と考えられる。

上記の性質を使うと、一様乱数$X_i$を$n$個加えた量を使って、 $$ Y = \frac{X_1 + X_2 + \cdots + X_n - n \mu}{\sqrt{n}\sigma} $$ を計算すれば($n$が10程度でも）正規分布$N(0,1)$に従う乱数を生成できることになる（ 計算速度を求めなければ、この方法は十分に実用的である。 ただし、一様乱数から正規分布する乱数を生成するアルゴリズムとしては Box-Mullerの方法が一般には良く使われている。）

# coding: utf-8
import random
import numpy as np
import matplotlib.pyplot as plt

ntrial = 10000

dice3=[ ]
dice5=[ ]
dice10=[ ]

for _ in range(ntrial):
    s3=0
    for _ in range(3):
        s3 = s3 + random.randint(1,6)
    dice3.append(s3)

    s5=0
    for _ in range(5):
        s5 = s5 + random.randint(1,6)
    dice5.append(s5)

    s10=0
    for _ in range(10):
        s10 = s10 + random.randint(1,6)
    dice10.append(s10)

bins = np.linspace(0, 100, 101)

plt.hist([dice3,dice5,dice10], bins, label=["n=3","n=5","n=10"])
plt.xlabel('sum')
plt.ylabel('Frequency')
plt.legend(loc='upper right')
plt.xlim(0,60)
plt.grid(True)
plt.show()

　練習：正規乱数の生成

上記のアルゴリズムに従い、1〜6の目を持つサイコロの値を加えることで、正規分布$N(0,1)$に従う乱数を発生させ、得られた頻度分布と正規分布 $$ f(y) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{y^2}{2}\right) $$ とを比較するプログラムを作成し、$n$の値を変えて、分布形の変化（両者の差異）を確認せよ。

　ヒント

サイコロの場合、平均$\mu=3.5$,分散 $\sigma^2 = \frac{(1-3.5)^2 + (2-3.5)^2 + \cdots + (6-3.5)^2}{6}=2.9166666\cdots$である。

$X_1 + X_2 + \cdots + X_n$の値が$x$であるような頻度が$p(x)$であったとしよう（ここで、$\sum_x p(x) = 1$とする）。 すると、変数変換 $y = (x - n \mu)/(\sqrt{n}\sigma)$ に対して、分布関数は $$ p(y)dy = p(y(x)) \left| \frac{dx}{dy} \right| dy $$ のように変換されるので、$f(y)$と比較すべきは $p(y(x)) \left| \frac{dx}{dy} \right|$ であることに注意 （ここで、$\frac{dx}{dy} = \sqrt{n} \sigma$）。