Pythonプログラミング（ステップ７・配列・線形代数）

NumPyライブラリ

線形代数等で学んだベクトルや行列の計算は、Pythonの標準的な機能のみで行うことは可能であるが、計算時間や記述の手間を省くためのライブラリとしてNumPyが広く使われている。プログラム中でNumPyの機能を使う際は、先立って、

import numpy as np

を宣言しておく必要がある。

NumPyでは、Python標準のリスト(list)に準じて、ベクトルや行列データを表現、操作することができる。 ただし、その実体はndarrayと呼ばれるオブジェクトであって†、リストとは異なる点も多いので、注意が必要である。

Pythonでベクトルを表現する流儀にはいくつかの選択肢があり得るが、ここでは、縦ベクトル $ \begin{pmatrix} 1 \\ 2 \\ 3 \\ \end{pmatrix} $ を、リスト

[ [1],
  [2],
  [3] ]

に、横ベクトル $ \begin{pmatrix} 1 & 2 & 3 \\ \end{pmatrix} $ を、[1,2,3] ではなく、

[ [1, 2, 3] ]

に対応させる。

また、行列 $ \begin{pmatrix} 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ \end{pmatrix} $ は、リスト

[ [1, 2],
  [2, 3],
  [3, 4] ]

に対応させる。

すなわち、列ベクトルは列数が1の、行ベクトルは行数が1の行列として、それぞれ表す。こうすることで、操作の一貫性を保つことができる。

ベクトルや行列の生成

NumPyの行列を生成するには、以下のようにリストから変換すればよい：

# 列ベクトル
v = np.array([ [1], [2], [3] ])

# 行ベクトル
h = np.array([ [1, 2, 3] ])

# 行列
A = np.array(
    [ [1, 2],
      [2, 3],
      [3, 4] ] )

ベクトルや行列の転置を取るには.T属性を用いればよい。例えば、行列 A の転置は A.T と表記する。 横ベクトルを h とすると、h.T はその縦ベクトルとなる。

int16
int32
int64
uint16
uint32
uint64
float32
float64	
float128

整数を要素とするリストからndarrayオブジェクトを生成すると、各要素が整数であるとして処理される （例えば、要素の値が1の場合に、それを2で除する演算を行うと、結果は0となる）。 要素を実数として扱う必要がある場合は、以下の例のように、dtype属性を付けて、そのことを明示するか、

# 実数の行列
X = np.array(
    [ [1, 2, 0],
      [0, 2, 3],
      [3, 0, 4] ], dtype='float64')

astype()属性によって型の変換を行う：

# 整数の行列
A = np.array(
    [ [1, 2, 0],
      [0, 2, 3],
      [3, 0, 4] ])
# 実数に変換
X = A.astype(dtype='float64')

任意の大きさの単位行列、ゼロ行列、要素が全て1の行列を生成することもできる：

# 単位行列
N = 100
E = np.eye(N)

# ゼロ行列
N = 32
M = 16
Z = np.zeros((N,M))

# オール1
W = np.ones((N,M))

NumPyには、いくつかの代表的な行列を生成する機能が内蔵されている。例えば、Vandermondeの行列 $$ V = \begin{pmatrix} 1 & x_1 & {x_1}^2 & {x_1}^3 & {x_1}^4\\ 1 & x_2 & {x_2}^2 & {x_2}^3 & {x_2}^4\\ 1 & x_3 & {x_3}^2 & {x_3}^3 & {x_3}^4\\ 1 & x_4 & {x_4}^2 & {x_4}^3 & {x_4}^4\\ \end{pmatrix} $$ を生成するには

x = np.array([1,3,5,7])
V = np.vander(x, increasing=True)

のように書けば事足りる。 その他の例についてはマニュアルを参照のこと。

非定型的な行列を生成するには、まずndarrayオブジェクトを生成し、要素毎に値を設定することになる。 規則性が高い場合は、リスト内表記なども使って、手短に記述できる場合もある。 一例として、巡回行列 $$ C = \begin{pmatrix} c_0 & c_1 & c_2 & c_3 & \cdots & c_{n-1} \\ c_{n-1} & c_0 & c_1 & c_2 & \cdots & c_{n-2} \\ c_{n-2} & c_{n-1} & c_2 & c_3 & \cdots & c_{n-3} \\ \vdots & & & & & \\ c_1 & c_2 & c_3 & c_4 & \cdots & c_{0} \\ \end{pmatrix} $$ を生成するコードを示す：

N=5
c = np.array([1,3,5,7,9])
C = np.row_stack([np.roll(c,i) for i in range(N)])

NumPyの配列（ndarray）のサイズは、shape属性として設定されている。

A = np.zeros((32,16))
print("行数=",A.shape[0], "列数=",A.shape[1])

行ベクトルや縦ベクトルを並べて行列を生成する例を以下に示す：

import numpy as np
# 行ベクトル a, bを生成
a = np.array([[1,2,3,4]])
b = np.array([[2,3,4,5]])
# 横ベクトルからの行列生成
C = np.concatenate([a,b])

# aとeを転置して縦ベクトルd,eを生成
d = a.T
e = b.T
# 縦ベクトルからの行列生成
D = np.concatenate([d,e],axis=1)

ベクトルや行列の和と差、スカラー倍

通常の数と同様に +演算や、-演算により、要素ごとの加減算が行われる。 ベクトルや行列のスカラー倍には、*演算子が使える。

e1 = np.array([[1],[2]])
e2 = np.array([[-2],[1]])
x = 3 * e1 + 2 * e2

部分行列、行や列の入れ替え

行列 $A$ の $i$ 行から $j$ 行、$k$ 列から $\ell$ 列までの範囲の部分行列を $B$ に設定するには

B = A[i:j+1,k:ell+1]

と記述する(A[i:j,k:ell]ではない点に注意)。

行列 $A$ の $i, j, k$ 行を取り出した部分行列を $C$、 $\ell, m, n$ 列を取り出した部分行列を $D$ に設定するには

C = A[[i,j,k],:]

D = B[:,[ell,m,n]]

行列 $A$の $i$行と$j$行を入れ替えるには

A[[j,i],:] = A[[i,j],:]

$k$行と$\ell$列を入れ替えるには

A[:,[ell,k]] = A[:,[k,ell]]

ベクトルと行列の積

このページでは、ベクトルは行列の一種として扱うことを前提にしているので、ベクトルの積や行列とベクトルの積も、行列同士の積として記述する。

行列 A と B の積は、ndarrayのdotメソッドを使って A.dot(B)と表現する。 なお、二次元行列に限れば、これを A.matmul(B)、あるいはその省略形であるA @ B と書いても同様の結果が得られる。

行列の積和演算の例として、行列 $A = \begin{pmatrix} 1 & 0.5 \\ -0.5 & 1 \\ \end{pmatrix} $について $e^{A}$ の値（の近似値） $$ S = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} + \sum_{k=1}^{10} \frac{A^k}{k!} $$ を求めるコードの例を以下に示す：

import numpy as np

A = np.array([[1,0.5],[-0.5,1]])
S = np.eye(2)
P = np.eye(2)
fact=1
for k in range(1,11):
    P = P.dot(A)
    fact = fact*k
    S = S + (1/fact) * P
print(S)

固有値と固有ベクトル

正方行列 $A$ の固有値と固有ベクトルは np.linalg.eig(A)で得られる。結果として、固有値と固有ベクトルが返される：

import numpy as np

A = np.array([
              [1,2,3],
              [2,1,2],
              [3,2,1]])
val,vec = np.linalg.eig(A)
print("eingen vaues=",val)
print("eingen vectors=",vec)

行列式、逆行列

正方行列 $A$ の行列式の値はnp.linalg.det(A)で、逆行列は np.linalg.inv(A)で得られる。

行列式の計算については、こちらのページも参照のこと。

行列$A$が、ある行列$P$を用いて $ P^{-1} A P = \begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \cdots & & & \\ 0 & 0 & \cdots & \lambda_n \\ \end{pmatrix} $ のように対角化できるとき、$P$として$A$の固有ベクトルを並べた行列に取れば良い。 このことを、数値的に確かめる例を以下に示す：

A = np.array([
              [1,2,3],
              [2,1,2],
              [3,2,1]])
evals, P = np.linalg.eig(A)
D = (np.linalg.inv(P)).dot(A).dot(P)
print(D)

１次方程式の解

$x$を未知ベクトルとする連立１次方程式 $A x = b$の解は np.linalg.solve(A,b)で得られる。

あるいは、$x = A^{-1} b$ であるから、np.linalg.inv(A).dot(b)としても同様の結果となる。

ライブラリを使わず、掃き出し法によって連立一次方程式を解くコードの例を以下に示す：

# coding: utf-8
# A X = B をガウスの消去法で解くコード

import numpy as np

A = np.array([
        [1,2,3,4],
        [2,4,1,3],
        [3,1,4,2],
        [3,4,2,1] ], dtype='float64')

B = np.array([
        [1],
        [3],
        [4],
        [2]], dtype='float64')

n = A.shape[0]

for i in range(n):
    k = np.argmax(np.abs(A[i:,i])) + i  # i以降の行のi列の要素のうちで絶対値が最大の行番号をkにセット
    if k!=i:
        A[[i,k],:] = A[[k,i],:]         # i行とk行を入れ替える
    aii=A[i,i]
    A[i,:] = A[i,:]/aii     # i行目の各要素を 1/aii倍
    B[i,0] = B[i,0]/aii
    for j in range(i+1,n) : # i+1行目以降について反復
        aji=A[j,i]
        A[j,:] = A[j,:] - A[i,:]*aji # i行目にajiを乗じた値をj行目から差し引く
        B[j,0] = B[j,0] - B[i,0]*aji

for i in range(n-1,0,-1): # 「下」から順に反復
    for j in range(0,i):  # iより「上」の行について反復
        aji=A[j,i]
        A[j,:] = A[j,:] - A[i,:]*aji # i行目にajiを乗じた値をj行目から差し引く
        B[j,0] = B[j,0] - B[i,0]*aji

# Bの要素が解になっている
print(B)

　解説: 結晶構造の解析

金属の結晶のように周期的な構造中に周期に近い波長の波が入射すると、結晶の周期と波の位相が揃うような条件で強い反射が起こる。 そして、その性質を使うことで、直接的な観察ができない微視的な結晶の構造を知ることができる。

結晶は繰り返しの単位となる原子配置毎に、結晶構造が定義されていて、３次元の場合は14種類の単位構造が知られている。 そして,、結晶中の全ての原子（格子点）の座標 $\boldsymbol{R}$ は、（格子点のどれかひとつを原点に選ぶと） 基本並進ベクトル（$\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3$）の整数倍($n_1, n_2, n_3$)の線形和で表現される。 $$ \boldsymbol{R} = n_1 \boldsymbol{a}_1 + n_2 \boldsymbol{a}_2 + n_3 \boldsymbol{a}_3 $$ 基本並進ベクトルは格子ベクトルの基底ベクトルであり、互いに直交しているとは限らない。

こうした構造の中に波数$\boldsymbol{k}$、角振動数$\omega$の電磁波が入射したとする。平面波の振幅は $$ E(\boldsymbol{r},t) = E_0 \exp(i \,\boldsymbol{k} \cdot \boldsymbol{r} - i \omega t ) $$ のように表すことができるから、原点の格子点と$\boldsymbol{R}$の格子点で常に波の位相が揃う条件（回折条件）が満たされるのは $$ \exp(i \,\boldsymbol{k} \cdot \boldsymbol{r} - i \omega t) = \exp(i \,\boldsymbol{k} \cdot (\boldsymbol{r} + \boldsymbol{R}) - i \omega t ) $$ すなわち、 $$ \exp(i\,\boldsymbol{k} \cdot \boldsymbol{R} ) = 1 $$ が成り立つ場合である（$\boldsymbol{k} \cdot \boldsymbol{R}$が$2 \pi$の整数倍になればよい)。

ここで、波数ベクトル $\boldsymbol{k}$の基底ベクトルの選び方について考える。 ３つの基底ベクトルを $\boldsymbol{b}_1, \boldsymbol{b}_2, \boldsymbol{b}_3$ と置くことにすると、 $$ \boldsymbol{b}_i \cdot \boldsymbol{a}_j = \delta_{ij} \tag{1} $$ となるように基底を選ぶことは常に可能である。

基本並進ベクトル（縦ベクトル）を並べた行列を $$ A = \begin{pmatrix} \boldsymbol{a}_1 & \boldsymbol{a}_2 & \boldsymbol{a}_3 \\ \end{pmatrix} $$ $\boldsymbol{k}$の基底を横ベクトルにして並べた行列を $$ B = \begin{pmatrix} \boldsymbol{b}^\top_1 \\ \boldsymbol{b}^\top_2 \\ \boldsymbol{b}^\top_3 \\ \end{pmatrix} $$ とすれば、(1)式は $$ B \, A = E $$ ($E$は単位ベクトル）に他ならないから $$ B = A^{-1} $$ すなわち、$A$の逆行列から横ベクトルを取り出して基底を構成すれば良い。

こうして構成された基底が張るベクトルを、結晶学では、逆格子ベクトルと呼んでいる。 逆格子ベクトル $\boldsymbol{K} = 2 \pi k_1 \boldsymbol{b}_1 + 2 \pi k_2 \boldsymbol{b}_2 + 2\pi k_3 \boldsymbol{b}_3$ を用いると、 回折の条件は $$ \boldsymbol{k} \cdot \boldsymbol{R} = \boldsymbol{K} \cdot \boldsymbol{R} = 2 \pi (k_1 n_1 + k_2 n_2 + k_3 n_3) $$ という風に簡単に表現できて、実に都合が良い。

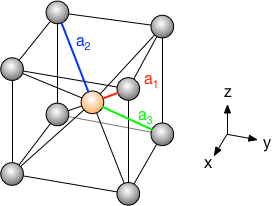
例として、格子定数1の体心立方格子を考えてみる。立方体の中央の格子点（オレンジ色）を原点に置くと、基本並進ベクトルとして $$ \boldsymbol{a}_1 = \begin{pmatrix} 1/2 \\ 1/2 \\ 1/2 \\ \end{pmatrix}, \; \boldsymbol{a}_2 = \begin{pmatrix} -1/2 \\ -1/2 \\ 　1/2 \\ \end{pmatrix}, \; \boldsymbol{a}_3 = \begin{pmatrix} -1/2 \\ 　1/2 \\ -1/2 \\ \end{pmatrix} \; $$ を選ぶことができる（他の組み合わせを選んでも構わない）。

これから、逆格子の基底ベクトルを求めるには、以下のように操作すればよい：

import numpy as np

a1 = np.array([[1/2],[1/2],[1/2]])
a2 = np.array([[-1/2],[-1/2],[1/2]])
a3 = np.array([[-1/2],[1/2],[-1/2]])

# 縦ベクトルから行列を生成
A = np.concatenate([a1,a2,a3],axis=1)

# 逆行列を計算
B = np.linalg.inv(A)

# Bから横ベクトルを抽出
b1 = B[0:1,:]
b2 = B[1:2,:]
b3 = B[2:3,:]

print(b1)
print(b2)
print(b3)

その結果は

[[0. 1. 1.]]
[[-1.  0.  1.]]
[[-1.  1.  0.]]

となり、これは（格子定数が2の）面心立方格子の基本並進ベクトルになっていることがわかる。

　練習：逆格子ベクトルの計算

面心立方格子の逆格子の基底ベクトルを上記と同様にして求めてみなさい。