Pythonプログラミング（ステップ８・行列の計算）

１．行列式の計算

数学（線形代数）の授業で行列式の計算を学んだ際に、何とも手間のかかることか、と、感じた諸君も多いのではなかろうか。 そういった面倒な計算はコンピュータにやらせるに限る。 まずは、効率は度外視して、「教科書通り」に計算する方法をPythonに移植してみよう。

例えば、第１列目に着目して行列式を余因子展開すると、 $$ \begin{eqnarray} \begin{vmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & & & & \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \end{vmatrix} & = & (-1)^{1+1} a_{11} \begin{vmatrix} a_{22} & a_{23} & \cdots & a_{2n} \\ a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & & & \\ a_{n2} & a_{n3} & \cdots & a_{nn} \end{vmatrix} \\ & + & (-1)^{2+1} a_{21} \begin{vmatrix} a_{12} & a_{13} & \cdots & a_{1n} \\ a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & & & \\ a_{n2} & a_{n3} & \cdots & a_{nn} \end{vmatrix} \\ & + & (-1)^{3+1} a_{31} \begin{vmatrix} a_{12} & a_{13} & \cdots & a_{1n} \\ a_{22} & a_{23} & \cdots & a_{2n} \\ \vdots & & & \\ a_{n2} & a_{n3} & \cdots & a_{nn} \end{vmatrix} + \cdots \end{eqnarray} $$ といった具合になり、サイズ$n$の行列の行列式が、サイズ$n-1$の行列式$n$個の計算に還元できる。

この様子を愚直にPythonコードに翻訳した例を以下に示す。

行列はPythonの二次元リストによって表現している。 リストの添字は0から始まるので、数学の教科書とは1だけ表記がずれているかもしれないが、符号の計算（$(-1)^{i+j}$）のところの表式は($i+j$のズレが2なので)そのままで構わない。

プログラム中では２つの関数を定義している。 cofactor(i,j,A)は、行列$A$の$i$行$j$列を取り除いた部分行列を生成するための関数、そして、 determinant(A)が行列式を計算する関数で、公式通りに、小行列式を再帰呼び出しで求めながら「総和」しているだけのシンプルな構造である。

# coding: utf-8

def submatrix(i,j,A):
    n = len(A[0])
    B = [ ]
    for k in range(n):
        if k==i:
            continue
        x=[ ] # gen row vector
        for l in range(n):
            if l==j:
                continue
            x.append(A[k][l])
        B.append(x)
    return B

# cofactor expansion
def determinant(A):
    n=len(A)
    if n==1:
        return A[0][0]
    det=0
    for i in range(n):
        det = det + (-1)**(i+0) * A[i][0] * determinant(submatrix(i,0,A))
    return det

# メイン部

X=[[1,3,2,4,5],
   [2,4,3,1,3],
   [3,1,2,3,4],
   [4,5,3,2,1],
   [5,2,1,4,3]]

d=determinant(X)

print(d)

　練習：行列式の計算量

上のコードでサイズ$n$の行列を計算する場合、関数determinant( )は何回呼び出されることになるか。

　練習：数式処理

上のコードを元にして

X=[['a','b','c','d'],
   ['e','f','g','h'],
   ['i','j','k','l'],
   ['m','n','o','p']]

のように、文字の行列を入力としてして与えたとき、記号の式の形で行列式を出力するよう改造してみなさい。

　ヒント

a*(e*i-h*f)-d*(b*i-h*c)+g*(b*f-e*c)

２．NumPyライブラリの利用

Pythonには、行列の計算をはじめとして、一般的・汎用的な計算を行うための「外付け」機能がいろいろと用意されている。 行列計算でよく使われているのがNumPy(ナン・パイ）である。 この節では、NumPyの基本的な使い方を紹介する。

もしまだなら、ウェブ等の情報を手がかりに、使っているシステムにまずNumPyをインストールする。そして、Pythonコードのはじめに

import numpy as np

と書く。こうしておくことで、np.何々 という名前でNumPyの機能が使えるようになる。

NumPyでは行列を ndarray という形式（オブジェクト）で管理する。これはリストに似ているものの、別物である。 ベクトルや行列を表現・生成するには、以下のようにする：

# 横（行）ベクトル
x = np.array([0.4, 0.1, -1.2])	

# 行列
A = np.array([
   [1,3,2,4,5],
   [2,4,3,1,3],
   [3,1,2,3,4],
   [4,5,3,2,1],
   [5,2,1,4,3]]
   )

# 7行7列の単位行列を生成
E = np.identity(7)

# 3行4列の行列を生成（各要素は0)
Z = np.zeros((3,4))

このように生成したデータにアクセスするには、リストの場合と同様、A[i][j] のように要素を指定できるほか、 ndarrayでは A[i,j] という表現も可能である。

NumPyには基本的な行列計算機能が備わっている。使い方は以下の例を見れば一目瞭然であろう。 ここで、行列の積の計算には .dot() を用いる点に注意。A * B は、要素毎に積をとった行列、という意味になる。

A = np.array([[1,2],[3,4]])
B = np.array([[-2,1],[1,-1]])

# 行列の和
C = A + B

# 差
D = A - B

# 行列の積 
F = A.dot(B)
G = B.dot(A)

# 転置
H = A.transpose()
# または
H = A.T

さらに、NumPyの中の線形代数(linalg)ライブラリをさらに読み込むことで、以下の関数が使えるようになる。 関数を呼び出す前に、

from numpy.linalg import det,inv,solve

のように、使用する関数をあらかじめインポートしておく。

diag()

trace()

det()

eig()

inv()

pinv()

qr()

svd()

solve()

lstsq()

以下に、線形代数ライブラリ関数を使って、行列式の計算と、連立方程式の解を２通りの方法で求めるコードの例を示す。

# coding: utf-8

import numpy as np
from numpy.linalg import det,solve,inv

A = np.array([
   [1,3,2,4,5],
   [2,4,3,1,3],
   [3,1,2,3,4],
   [4,5,3,2,1],
   [5,2,1,4,3]]
   )
b = np.array([1,0,0,0,1])

# 行列式の計算
print(det(A))

# 連立方程式 A x = b を解く
x = solve(A,b)
print(x)

# 今度は、A^{-1} b で解を計算する
x2 = inv(A).dot(b)
print(x2)

# 両者の自乗差をチェックする
diff = (x-x2).dot((x-x2))
print(diff)

　練習：行列式ふたたび

このページの最初の余因子展開による行列式の計算結果を、NumPyで検算してみなさい。

サイズの大きな行列（8程度以上）を用意し、両者の計算時間も比較してみなさい。

　ヒント

import numpy as np

A = np.random.uniform(-1, 1, (10, 10))

X = A.tolist()

　解説: ランダム行列の固有値分布

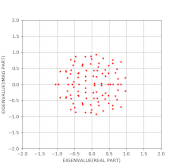
上のヒントで、検算のためにランダムな行列を生成する方法を紹介したが、ランダムな行列の振る舞い方には興味深い「規則性」がいろいろと見つかっている。 例えば、各要素が、平均0で、分散 $1/n$ のガウス分布するようなランダムな値の $n \times n$ 正方行列の固有値を複素平面にプロットすると、 $n$ が大きい場合、半径１の円の内部に一様に分布することがわかっている （円則(circular law)）。

その様子を、NumPyとmatplotlibを使って確認するコードの例を以下に示す：

# coding: utf-8
import math
import numpy as np
from numpy.linalg import eig
import matplotlib.pyplot as plt

n = 100

A = np.random.normal(0, 1/math.sqrt(n), (n, n))

z,v = eig(A)

xdata = np.real(z)
ydata = np.imag(z)

plt.plot(xdata,ydata, '.', color=(1.0,0,0.0))
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.xlabel('EIGENVALUE(REAL PART)')
plt.ylabel('EIGENVALUE(IMAG PART)')
plt.grid(True)
plt.show()

この例の中では、関数 np.random.normal(平均, 標準偏差, (行数, 列数))によって、正規（ガウス）分布に従うランダム行列を生成している。