情報基礎「Pythonプログラミング」（書を携えて家に籠ろう）

Pythonプログラミング（書を携えて家に籠ろう）

このページでは、（Pythonの学習とは関係ありませんが）新型コロナウィルスの感染拡大防止のために「自宅待機」が有効と期待できる理由について考えてみる。

感染が拡大する基本的なメカニズムと基本再生産数

感染症が拡大するのは、患者がまだ病気になっていない人に病原体（ウイルス）を移すからである。ここで、『病気にかかっている間に、何人と接触して病気をうつすか』 が重要になってくる。

完治するまでに、１人にしかうつさなかったとすると、バトンリレーのように、患者の数は１人のままで、それ以上増えることはない。

もし、治るまでに２人にうつすとすると、倍々ゲームで、患者数が激増するのは明らかである。

治るまでに 0.5人にしかうつさないとすると（うつす確率が0.5）、いずれ感染は止まるはずである。

この「倍率」は基本再生算数 $R_0$ と呼ばれている。新型コロナウィルスの場合、$R_0$は2よりも大きいと言われているので、倍々（あるいはそれ以上）の勢いで患者数が増えてしまうわけである。

$$ \textrm{基本再生産数} = \frac{\textrm{完治するまでに要する日数 }}{\textrm{人との接触の間隔（日）}} = \textrm{感染の倍率} $$

基本再生産数を下げるための方策

感染を止めるには、感染してしまった人が、完治するまでに、新たな感染を１人以上引き起こさないことが重要である。同じことだが、罹患していない人が患者に接する頻度を、病気が完治するくらい（数週間程度）の間に１回程度以下に押さえる必要がある、とも言い換えられる。

そこで、無自覚な人も含めた患者、そして健康な人、いずれも、人との接触の機会を減らす努力が求められているわけである。

ここで、人との接触の機会（頻度）を減らす以外にも、もうひとつ重要な注意点がある。それは、移動をできるだけ減らす、という観点である。

同じ接触頻度であったとしても、隣近所の人たちとしか会わないのであれば、もし不幸にも感染者が出てしまったとしても、拡大の仕方は比較的緩やかなものとなるだろう。

それはちょうど森林火災に例えることができる。炎を上げて燃えている木が感染者、燃え落ちてしまった場所が回復者（または死者）と考えれば、感染（火災）は、その規模を別とすれば、「徐々に」しか広がらないはずである。

ところが、火の粉が数十キロメートル先まで飛んで、あちこちで新たな火災を引き起こすとしたら、火災はあっという間に全土に広がってしまうだろう。これは、人々が飛行機や電車で遠くまで移動し接触する状況に対応する。

おもちゃモデル

現実の世界とはかなりかけ離れてはいるものの、移動の抑制の効果について感じをつかむために、以下のような「おもちゃモデル」を考えてみよう。

ここでは、人々の「家」からの移動は、標準偏差$\sigma$のガウス分布に従うと仮定する。

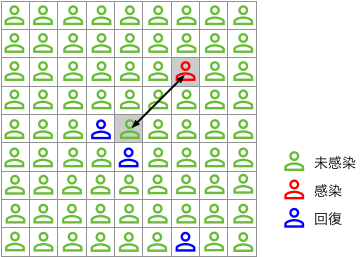
人々は碁板のマス目状の世界に暮らしており、買い物や、通勤などのため、一定時間間隔で移動する。人々の行動は「自宅」を起点としてマス目を単位としたある距離の範囲に制限されており、その中でランダムに人との接触を繰り返す。その平均的な移動距離を$\sigma$で表すことにしよう。

そして、初期に、ごく少数の感染者が分布してるような状況を想定し、接触した相手が運悪く発病していた場合は、自分も感染してしまう。

$\sigma$を1, 3, 10, 30にそれぞれ変えてシミュレーションした結果の例が以下の動画である。いずれの場合も、基本再生産数$R_0$は 2.5 で、日本の新型コロナウイルスの感染もこれくらいの値ではないかと言われている。 $\sigma=1$が自宅の向こう三軒両隣としか接触しないような状況とすれば、$\sigma=30$は近隣の職場やスーパーと自由に往来できるような状況を模していると言えるかもしれない。

注目すべきは、移動距離が小さい場合は、基本再生算数が1より大きくても、感染の拡大が緩慢になる（場合によっては終息する）という点である。仮に患者が周囲に感染させても、回復者がさらなる感染を「ブロック」するので、それ以上の拡大にブレーキがかかる。できるだけ移動を控えるべき理由が、ここからも想像できる。

当面のあいだは、書を携えて家に籠ろう！

基本再生産数 $R_0 = 2.5$ の場合のシミュレーション

モデルについてはこちらを参照

シミュレーションに用いたPythonコード

実行にはpyglet(バージョン1.5.27以前）が必要です

# coding: utf-8
import pyglet
from pyglet.gl import *
import random
import math
import numpy as np

# グローバル変数
p0=0.0005 # 初期感染密度
N=100     # １辺の格子数
r0=2.5    # 基本再生産数
SCALE=10  # 格子のサイズ
sigma=1   # 平均的な移動距離

gamma = 1.0/r0
s=np.zeros([N,N])
counter=0
n_i=0

# 初期化
def init_state():
    global s,n_i
    for i in range(N):
        for j in range(N):
            if random.random()<p0:
                s[i,j] = 1
                n_i += 1

# 状態更新
def update_state(n):
    global s,counter,n_i
    for _ in range(n):
        i = random.randrange(0,N,1)
        j = random.randrange(0,N,1)
        if s[i,j]==0:
            di = int(random.gauss(0,sigma))
            dj = int(random.gauss(0,sigma))
            i2 = (i+di) % N
            j2 = (j+dj) % N
            if s[i2,j2]==1:
                s[i,j]=1
                n_i += 1
        elif s[i,j]==1:
            if random.random()<gamma:
                s[i,j]=2
                n_i -= 1
        counter += 1

def next_frame(dt):
    return

def redraw():
    update_state(1000)
    for i in range(N):
        for j in range(N):
            if s[i,j]==0:
                glColor3d(0.2,0.6,0.7)
            elif s[i,j]==1:
                glColor3d(0.8,0.3,0.1)
            else:
                glColor3d(0.2,0.2,0.2)

            glBegin(GL_POLYGON)
            glVertex2d((i+0)*SCALE,(j+0)*SCALE)
            glVertex2d((i+1)*SCALE,(j+0)*SCALE)
            glVertex2d((i+1)*SCALE,(j+1)*SCALE)
            glVertex2d((i+0)*SCALE,(j+1)*SCALE)
            glEnd()

    t = counter/(N*N)
    r_i = n_i/(N*N)
    label = pyglet.text.Label('t='+str(t)+'   I='+str(r_i), 
                              font_name='Helvetica', color=(255,255,255,255),
                              font_size=12, x=10, y=10)
    label.draw()


init_state()
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
win.set_caption('SIR Model in 2d')

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0,1)
    redraw()

pyglet.clock.schedule_interval(next_frame, 1/10.0)
pyglet.app.run()