Pythonプログラミング（ステップ７・多変数のニュートン法）

このページでは、多変数の方程式の数値解法（ニュートン法）について考える。

多変数の場合のニュートン法

ニュートン法は非線形な方程式を解く場合に非常に協力なツールである。１変数の場合についてはこちらのページで説明したが、 ２変数以上の問題についても、同様の手続きで連立方程式の根を求めることができる。

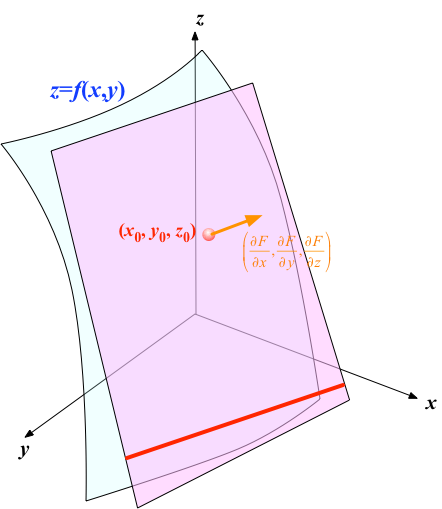
ここでは、２変数関数の連立方程式 $$ \begin{eqnarray} f(x,y) = 0\\ g(x,y) = 0 \end{eqnarray} $$ の解 $x, y$を求める方法について考えることにする。 $f$を点$(x,y)$からの「高さ」$z$ と考え、$f$が表す曲面を想像してみよう。 $$ F(x,y,z) = f(x,y) - z = 0 $$ とおくと、点$(x_0,y_0,z_0)$で曲面に接する平面の方程式は $$ \frac{\partial F(x_0,y_0,z_0)}{\partial x} (x-x_0) + \frac{\partial F(x_0,y_0,z_0)}{\partial y} (y-y_0) + \frac{\partial F(x_0,y_0,z_0)}{\partial z} (z-z_0) = 0 $$ で与えられるから、すなわち $$ \frac{\partial f(x_0,y_0)}{\partial x} (x-x_0) + \frac{\partial f(x_0,y_0)}{\partial y} (y-y_0) - (z-f(x_0,y_0)) = 0 $$ となる。 よって、x,y平面（高さが$z=0$）と、この接平面の交差は、 $$ \frac{\partial f(x_0,y_0)}{\partial x} (x-x_0) + \frac{\partial f(x_0,y_0)}{\partial y} (y-y_0) = - f(x_0,y_0) $$ で与えられる。

また$g$についても全く同様に $$ \frac{\partial g(x_0,y_0)}{\partial x} (x-x_0) + \frac{\partial g(x_0,y_0)}{\partial y} (y-y_0) = - g(x_0,y_0) $$ となる。

２つの接平面とx,y平面（高さ0）とが交差する点$(x,y)$は、行列で表現し直すと、式 $$ \left( \begin{array}{cc} \frac{\partial f(x_0,y_0)}{\partial x} & \frac{\partial f(x_0,y_0)}{\partial y} \\ \frac{\partial g(x_0,y_0)}{\partial x} & \frac{\partial g(x_0,y_0)}{\partial y} \end{array} \right) \left( \begin{array}{c} x - x_0 \\ y - y_0 \end{array} \right) = - \left( \begin{array}{c} f(x_0,y_0) \\ g(x_0,y_0) \end{array} \right) \tag{1} $$ を満たさなければならない。

ヤコビ行列を$J$とし、ベクトルを $$ \boldsymbol{x} = \left( \begin{array}{c} x \\ y \end{array} \right) $$ $$ \boldsymbol{f}(\boldsymbol{x}) = \left( \begin{array}{c} f(x,y) \\ g(x,y) \end{array} \right) $$ と定義すれば、式(1)は $$ J \left[ \boldsymbol{x} - \boldsymbol{x}_0 \right] = - \boldsymbol{f}(\boldsymbol{x}_0) \tag{2} $$ となるから、$J$の逆行列$J^{-1}$を使って、高さ0の面との交点が $$ \boldsymbol{x} = \boldsymbol{x}_0 - J^{-1} \boldsymbol{f}(\boldsymbol{x}_0) $$ で得られる。3変数以上の場合も全く同様である。

この過程を $$ \boldsymbol{x}_{k+1} \leftarrow \boldsymbol{x}_k - J^{-1} \boldsymbol{f}(\boldsymbol{x}_k) \tag{3} $$ のように反復することで、 $\boldsymbol{f}(\boldsymbol{x}) = \boldsymbol{0}$ の根を効率的に求めることができる（多変数のニュートン法）。

２次方程式の解

では、上記のやり方で、$w$の２次方程式 $$ w^2 + a w + b = 0 $$ の２根を$x,y$を、解の公式に頼らずに求めてみよう。２次方程式の解と係数の関係から $$ \begin{eqnarray} f(x,y) = x + y + a = 0\\ g(x,y) = x y - b = 0 \end{eqnarray} $$ となる。ヤコビ行列は $$ J = \left( \begin{array}{cc} 1 & 1 \\ y & x \end{array} \right) $$ であり、その逆行列は $$ J^{-1} = \frac{1}{x-y} \left( \begin{array}{cc} x & -1 \\ -y & 1 \end{array} \right) $$ これを使って式(3)に従って反復すると、２つの解が同時に求まる（ただし、重根を持つ場合は逆行列が求まらないので、この方法は使えない）。

# coding: utf-8

a = -5
b = 6
eps = 1.0E-8

def f(x,y):
    return x+y+a

def g(x,y):
    return x*y-b

x=0
y=1
for _ in range(20):
    x2 = x - ( x*f(x,y) - 1*g(x,y))/(x-y)
    y2 = y - (-y*f(x,y) + 1*g(x,y))/(x-y)
    if (x2-x)**2 + (y2-y)**2 < eps**2:
        break
    x=x2
    y=y2

print(x2,y2)

　練習：三次方程式の数値解

２次方程式の例に倣って、３つの異なる実根を持つ三次方程式をニュートン法で解くコードを作成し、動作を確認してみなさい。

　ヒント

ラグランジュの未定乗数法

２変数の関数 $f(x,y)$ が与えられているとき、別の関数が $g(x,y)=0$ となる状況で、$f$を最大にするような$(x,y)$の組を求めたい。 このとき $g(x,y)=0$ を拘束条件と呼ぶ。

例えば、放物面 $f(x,y)= -(x^2+y^2)$ を考えると、拘束条件がなければ、$f$が最大になるのは明らかに$(0,0)$である。

ここで、$g(x,y) = x + y - 1$ として、拘束条件 $g(x,y)=0$ を与えると、$y = 1 - x$であるから、 $$ f(x,y) = -x^2 - (1-x)^2 = -2 x^2 + 2 x - 1 = -2 (x - 1/2)^2 - 1/2 $$ となり、$x=1/2$、$y=1-1/2=1/2$で$f$が最大となることがわかる。

ところが、拘束条件が複雑な場合、例えば $g(x,y)= \tanh(x) + \tanh(y) - 1$ のように非線形の場合や、変数の数が増えると、直接的に解くのは難しい。

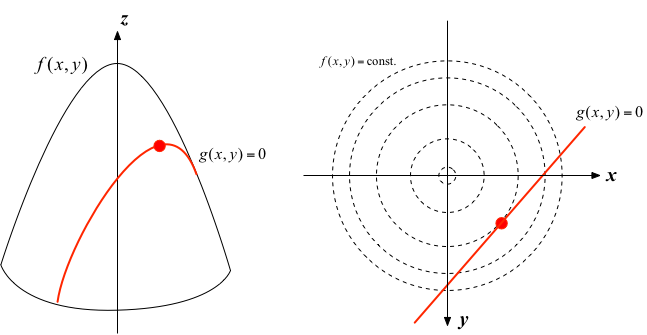
そこで、もう少し一般的に考えてみよう。 $f(x,y)$を「高さ $z$」であると考えると、図のように、山のような地形（放物面）を描くことができる。 その面上に$g(x,y)=0$を満たす「山道」描いてみよう（赤色の線）。すると、山道上の高さが最大となる点（つまり$f$が最大化される点）は、 x,y面上で、道の方向と山の等高線がちょうど平行になるようなところ、になることが分かる。

「山の等高線と山道の方向が並行になる」は、90度だけ方向を変えて表現し直せば、「山の勾配方向と山道の法線が並行になる」と言っても構わない。 山の勾配は、ベクトル $$ \textrm{grad}\, f= \left( \begin{array}{c} \frac{\partial f(x,y)}{\partial x} \\ \frac{\partial f(x,y)}{\partial y} \end{array} \right) $$ で表すことができる。 一方、山道の法線方向も同様に $$ \textrm{grad}\, g= \left( \begin{array}{c} \frac{\partial g(x,y)}{\partial x} \\ \frac{\partial g(x,y)}{\partial y} \end{array} \right) $$ となる。両者が並行になるとは２つのベクトルの向きが揃うことに他ならないから、比例定数を$\lambda$として、 $$ \textrm{grad}\; f = \lambda \, \textrm{grad}\; g $$ あるいは $$ \textrm{grad}\, \left\{ f + \lambda\, g \right\} = \boldsymbol{0} $$ と表現できる。 この表式は、変数の数が増えても全く変わらない。 このようにして拘束条件付きの多変数関数の最大値（最小値）を求める方法を、ラグランジュの未定乗数法と呼ぶ。 ここで、未定定数とは「とりあえずの比例定数」として導入された$\lambda$のことを指す。

目的関数 $f(x,y)= -x^2 -y^2$, 拘束条件 $g(x,y)= \tanh(x) + \tanh(y) - 1 = 0$ の場合に当てはめると、 $f$が最大になるための条件は $$ \begin{eqnarray} \frac{\partial}{\partial x} \left\{ -x^2-y^2 + \lambda \, (\tanh(x) + \tanh(y) - 1) \right\} =0\\ \frac{\partial}{\partial y} \left\{ -x^2-y^2 + \lambda \, (\tanh(x) + \tanh(y) - 1) \right\} =0 \end{eqnarray} $$ となる。実際に微分を行うと、 $$ \begin{eqnarray} -2 x + \lambda \,(1- \tanh^2(x)) = 0\\ -2 y + \lambda \,(1- \tanh^2(y)) = 0 \end{eqnarray} $$ これと、拘束条件 $$ \tanh(x) + \tanh(y) - 1 = 0 $$ を連立させて解くことで、$f$を最大にする$x, y$、 そして未定定数の $\lambda$ を求めることができる （ただし、容易に連立方程式の解が見つかるかどうかは別の話である）。

　練習：非線形連立方程式

上記の問題について、具体的な数値解を求めてみなさい。 $$ \begin{eqnarray} F(x,z) = -2 x + z \,(1- \tanh^2(x)) = 0\\ G(y,z) = -2 y + z \,(1- \tanh^2(y)) = 0\\ H(x,y) = \tanh(x) + \tanh(y) - 1 = 0 \end{eqnarray} $$ と置いて、ニュートン法を用いること。

　解説: SciPyの利用

理工学分野で良く使われる数値計算をまとめ、Pythonから簡単に呼び出せるようにパッケージ化したのがSciPyである。 SciPyの中のoptimizeパッケージの中にはニュートン法を含め、方程式の根を求めるアルゴリズムが複数、利用可能である。

元々のニュートン法は、ヤコビ行列（関数の偏微分）を求め、連立方程式(2)を、反復の都度、解かなければならないが、大規模な問題になると、なかなか大変である。 そこで、偏微分を差分で近似し、連立方程式をクリロフ部分空間法と呼ばれる効率のよい方法で解くことができる関数がSciPyには含まれている。 以下はそのコードの例である：

# coding: utf-8

import math
from scipy.optimize import newton_krylov

def F(x):
    return [
        -2 * x[0] + x[2]*(1-math.tanh(x[0])**2),
         -2 * x[1] + x[2]*(1-math.tanh(x[1])**2),
         math.tanh(x[0]) + math.tanh(x[1]) - 1
         ]

guess = [1,1,0]

sol = newton_krylov(F, guess, method='lgmres')

print(sol)

コードの補足