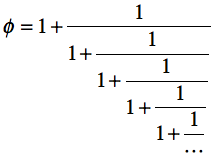Pythonプログラミング（ステップ４・ニュートン法）

このページは、方程式の数値解を反復によって求める方法について考える。

１．反復によって方程式を解く

二次方程式 $x^2 - x - 1 =0$ の解を求める方法について考えてみよう。もちろん我々は解の公式を知っているので、直ちに $$ x = \frac{1 \pm \sqrt{5}}{2} $$ で一件落着なのだが、仮に、解の公式を知らず、しかも、数値的に値が求まれば十分、といったケースをここでは想定する。 事実、世の中には「解の公式」が無い（まだ見つかっていない、仮に見つかったとして複雑すぎて使えない、あるいは、公式そのものが存在しない）場合がほとんどである。

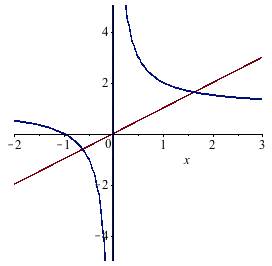
まず、元々の方程式を少し変形して $$ x = 1 + \frac{1}{x} $$ と書き直してみる。そして、その右辺と左辺をそれぞれ $x$ の関数だと思ってプロットすると、以下のようになる（茶色が$x$、青が$1+1/x$)。

このとき、二つの線の交点の $x$ の値を求めることができれば、方程式が解けたことになる。

そのアルゴリズムは案外と単純である：

• 1: $x$の出発値をセットする
• 2: $x^\prime \leftarrow 1 + 1/x$
• 3: 値の変化量 $\left| x^\prime - x \right|$ が十分小さい値になれば反復を終了し、5:に進む
• 4: $x^\prime$ を改めて $x$とおいて、2:からを繰り返す
• 5: 解として $x^\prime$ を出力し、終了する

実は、このパターンの計算はすでに登場していて、連分数

の例題プログラム4cが、まさに「これ」である。

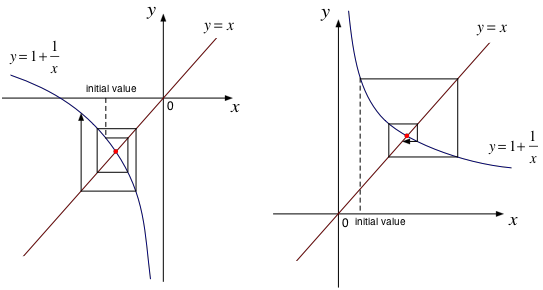
ここで、注意深い諸君は、上の計算では二次方程式の２つの解のどちらが求まるのか（あるいは両方求まるのか）が気になるだろう。 それについて考えるため、「まず $x$ の出発値を選んでおいてから、$1+1/x$ を新しい $x$ だと考えて繰り返す」というプロセスを図で表してみたのが以下である。 波線は出発値のセット、矢印付きの線分は反復を表している。 図の左側では反復の度に交点から遠ざかる一方で、右側では値が交点に収束するように見える。

つまり、上記の計算法によって求めることができるのは、解のうち片方（図で右側の$(1 + \sqrt{5})/2$)だけなのだ。

この違いは、交点 $x=x^*$ での関数 $y(x)=1+1/x$ の傾きの大きさによって決まり、以下で述べるように、$\left| y'(x^*) \right| < 1$ であれば、値が交点（固定点と呼ぶ）に収束することがわかる。

以上で述べた方程式を解くための手順を、もう少し一般化してまとめると、

• 元々の方程式 $f(x)=0$ を変形して $x=y(x)$ のパターンにする
• 解の近傍に出発値を設定した上で、$x \leftarrow y(x)$ を反復し、解 $x=x^*$ に収束させる
• ただし、$\left| y'(x^*) \right| < 1$ の条件が満たされていないと、この方法では解に収束しない*

となる。

* ということは、$x=y(x)$ のパターンの作り方を工夫することで、別の解まで探し出すことができる可能性がある。 例えば、上の二次方程式の例では、$z=1/x$ と変数変換してから、$z \leftarrow 1/z - 1$ を反復すると、他方の解を得ることができる。

　練習：非線形方程式の数値解

反復法を使って、非線形方程式 $\exp(-x) - \frac{x}{x+1}=0$ の解を求めるプログラムを作成し、動作を確認せよ。

　ヒント

解は $x=-1.349976485 \cdots$ 、および $x= 0.8064659942\cdots$ である。

　解説 : 固定点の安定性

解くべき方程式 $x=y(x)$ を見ると、これは、関数 $y(x)$ の値が再び $x$ になっている状態を探すことに他ならず、 そのような $x=x^*$ は $y(x)$ の固定点(fixed point)と呼ばれる。 いま、反復の過程で、固定点の近くの $x=x^* + \delta$ の状態にあったとすると、次の反復では、値は $y(x^* + \delta)$ に更新される。 固定点の周りで $y(x)$ を展開し、$y(x^*)=x^*$ であることを思い出して、式を整理すると $$ y(x^* + \delta) = x^* + y'(x^*) \delta + O(\delta^2) $$ となる。これは、最初の「ずれ」$\delta$が、反復の過程で（高次の項が無視できるような状況では） $$ \delta \to y'(x^*) \delta $$ と変換されることに対応する（$y(x)$ は $x=x^*$ の近傍で縮小写像になっている）。つまり、$n$回の反復で、「ずれ」は $(y'(x^*))^n \delta$ のように変化することになるので、 それが$0$に収束するための条件（あるいは、固定点が安定である条件）は $\left| y'(x^*) \right| < 1$ となる。

２．ニュートン法による求根

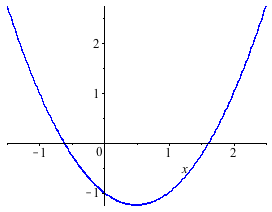
ここで、再び $x^2 - x - 1 = 0$ の数値解法を考えよう。 $f(x)=x^2-x-1$ とおいて、$y=f(x)$ をプロットすると下図のようになるが、x軸とグラフの交点の位置を我々は求めたいわけである。

この種の問題に対しては、ニュートン法（Newton's method)と呼ばれる、非常に効率のよい反復法のアルゴリズムが知られている。 その手順はそれほど難しいものではない：

• 1: $x$ の出発値をセットする
• 2: その位置で $y=f(x)$ の接線を引き、接線がx軸と交叉する点の $x^\prime$ の値を求める
• 3: 値の変化量 $\left| x^\prime - x \right|$ が十分小さい値になれば反復を終了し、5:に進む
• 4: $x^\prime$ を改めて $x$とおいて、2:からを繰り返す
• 5: 解として $x^\prime$ を出力し、終了する

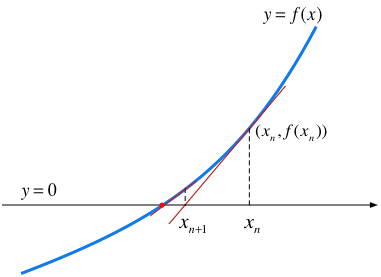
ここで、より具体的な計算手順を得るために、$n$ 回目の反復の際の $x$ の値を $x_n$ と置いて、反復の過程を考えてみよう。 まず、ステップ２〜４の反復の様子を図で表すと、次のようになる。赤線が接線である。

ここで、座標 $(x_n,f(x_n))$ を通り、勾配が $f'(x_n)$ の直線の方程式は $$ y = f'(x_n) (x - x_n) + f(x_n) $$ であるから、この式で $y=0$ とおいて、$x$ について解くと、 $$ x = x_n - \frac{f(x_n)}{f'(x_n)} $$ となる。この値を、次のステップの$x$とするわけだから、ニュートン法の反復の「ステップ２」では、 $$ x_{n+1} \leftarrow x_n - \frac{f(x_n)}{f'(x_n)} $$ という処理を行えばよいことが分かった。

例えば、$f(x)=x^2-x-1$ の場合、その導関数は $f'(x)=2x-1$ とすぐ計算できるので、具体的なコードは以下のようになるだろう：

# coding:utf-8
import math

x=float(input("出発値:"))
while True:
    xp = x - (x*x-x-1)/(2*x-1)
    if abs(xp-x)<0.00001:
       break
    x = xp

print("x=",xp)

　練習：ニュートン法（その１）

Pythonの関数機能math.sqrt( )を使わないで、 任意の正の$x$について $\frac{1}{\sqrt{x}}$ をニュートン法で計算するプログラムを作成してみなさい。

　練習：ニュートン法（その２）

ニュートン法を使って、非線形方程式 $\exp(-x) - \frac{x}{x+1}=0$ の解を求めるプログラムを作成し、動作を確認せよ。

　解説 : ニュートン法の収束性

ニュートン法で $f(x)=0$ の数値解を計算する際、$n$回目の反復を行なった時点で、解 $x^*$ からまだ $\delta$ だけずれていた、すなわち、 $$ x_n = x^* + \delta $$ であったとしよう。

この状態で、さらに反復を続けると、次のステップでは $$ x_{n+1} = x^* + \delta - \frac{f(x^* + \delta)}{f'(x^* + \delta)} $$ となるが、関数を$x^*$の周りでテイラー展開 $$ \begin{eqnarray} f(x^*+\delta) = f(x^*) + f'(x^*) \delta + \frac{1}{2} f''(x^*)\delta^2 + O(\delta^3), \\ f'(x^*+\delta) = f'(x^*) + f''(x^*) \delta + O(\delta^2) \end{eqnarray} $$ して、定義から $f(x^*)=0$ であることを思い出しながら、式を整理すると $$ x_{n+1} = x^* + \frac{1}{2} \frac{f''(x^*)}{f'(x^*)} \delta^2 + O(\delta^3) $$ となる（$\delta$の一乗の項は相殺されて消えるところがミソである）。

つまり、テイラー展開で $\delta$ の3次以上の項が無視できるくらいに $|\delta|$ が十分小さければ、1回の反復によって、誤差が $\delta$の２乗に依存して、 $$ \delta \to \frac{1}{2} \frac{f''(x^*)}{f'(x^*)} \delta^2 $$ のように変化することになる。 このことは（感覚的には）誤差が $1/10 \to 1/100 \to 1/10000 \to \cdots$ と急激に減少することを意味している。

　解説 : 割線法

ニュートン法では各点での関数の微分があらかじめ分かっている必要があるが、その計算に手間がかかるような場合は、微分を $$ f'(x_n) \approx \frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}} $$ で近似して、 $$ x_{n+1} \leftarrow x_n - \frac{f(x_n) (x_n - x_{n-1})}{f(x_n) - f(x_{n-1})} $$ を反復する方法も有効である。これは割線法（secant method)と呼ばれる。 微分を差で近似する「ズル」の代償として、ニュートン法に比べて収束は若干遅い（誤差は$\delta^{1.61}$程度で減少する）ことが分かっている。

亀場で練習：反復写像

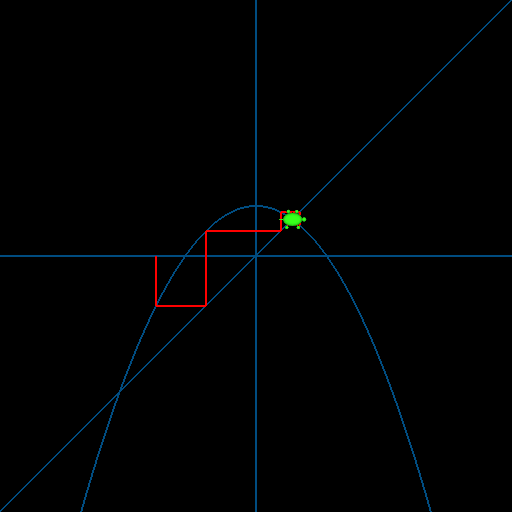
$x$ の方程式 $x^2/100 +x-C = 0$ の解をこのページで説明した反復法で解こうと考え、$y(x)=-x^2/100+C$ とおいた。 下図は、$C=50$ の場合に、$x$の出発値を-100とおいて反復計算を行った過程を亀場を使って表示した例である。

これと同様にして、反復を亀の軌跡によって可視化するプログラムを作成してみよ。さらに、$C$ の値を色々と変え、亀の挙動を観察してみよ（例えば$C=150$）。

　ヒント