Pythonプログラミング(ステップ6・SIRモデル・補足)
このページでは、Pythonの学習とは関係無いが、伝染病の流行の基本的なモデルであるSIRモデルを、潜伏期間を考慮したモデルに拡張する方法について、あれこれ考えてみる。(このページは書きかけ)
潜伏期間まで考えたモデル:SEIRモデル
罹患していない人(S)が感染者(I)と接触しても、感染力を持つまでには一定の時間がかかると言われている。 つまり、SとIが接触しても、その時点ではまだIには変化せず、暴露された(exposed)状態 E に一旦変わり、その後、潜伏期を経て、Iに変化する、というのがより現実的なプロセスである。 そこで、$t$日目でのEの状態の人数を新たな変数$w(t)$で表現することにしよう。 また、Sの人数を $x(t)$, Iを$y(t)$、そしてRを$z(t)$と置く。
この様子を化学反応に倣って表すと、以下のとおり: $$ \begin{eqnarray} \textrm{S} + \textrm{I} & \to & \textrm{E} + \textrm{I} \\ \textrm{E} & \to & \textrm{I} \\ \textrm{I} & \to & \textrm{R} \end{eqnarray} $$
SIRモデルの考察と同様に、$t$日目から$t+\Delta t$日目の間にSとIの接触によって、Eは $$ \beta \, x(t) \, y(t) \, \Delta t $$ だけ増加する。 その一方で、 現在から$\tau$だけ過去のEが、どれくらいの重みでIの生成に寄与するかを、関数$f(\tau)$で表することにして、 潜伏期が「明けた」者が I へと状態が遷移することによる E の減少分を畳み込み $$ - \int_0^{t} w(t-\tau) \, f(\tau) \, d\tau \Delta t = - \int_{0}^{t} w(t') \, f(t-t') \, dt' \Delta t $$ で表すことにする。すると、$w(t)$の変化率は $$ \frac{dw(t)}{dt} = \beta \, x(t) \, y(t) - \int_{0}^{t} w(t') \, f(t-t') \, dt' \tag{1} $$ となる。
ここで、$f(\tau)$ がそのまま潜伏期間の分布を表しているわけではない点に注意したい。
最も単純な例 $f(\tau) = \sigma \delta(\tau)$ について考えてみよう。 初期値$w(0)$で、感染者が全くいない $y(t)=0$ とすると $$ \frac{dw(t)}{dt} = - \sigma w(t) $$ すなわち $$ w(t) = w(0) \exp(-\sigma t) $$ 符号と規格化定数を別にすれば、$w(t)$ の時間変化率が潜伏時間の分布に他ならないので、この場合、潜伏期間は指数分布となることがわかる (潜伏期間の平均は$1/\sigma$)。
実際に、$f(\tau) = \sigma \delta(\tau)$と置いたモデルは SEIR モデルとして知られている: $$ \begin{eqnarray} \frac{dx(t)}{dt} & = & - \beta \, x(t) \, y(t) \\ \frac{dw(t)}{dt} & = & \beta \, x(t) \, y(t) - \sigma w(t) \\ \frac{dy(t)}{dt} & = & \sigma w(t) - \gamma y(t) \\ \frac{dz(t)}{dt} & = & \gamma y(t) \end{eqnarray} $$
以上の考察から、SEIRモデルは、潜伏期間が平均 $1/\sigma$ で指数分布する場合のモデルである。
時間遅れを陽に取り入れたSEIRモデルの拡張
病原体が長期間体内に潜むような場合は、時間遅れ$T$を陽に入れて $$ f(\tau) = \sigma \, \delta(\tau - T) $$ としたほうが、現象をよく記述できる可能性がある。その場合、Eの変動は形式的に $$ \frac{dw(t)}{dt} = \beta \, x(t) \, y(t) - \sigma \, w(t-T) $$ となる。
簡単のため、初期の感染者がいない($y=0$)場合 $$ \frac{dw(t)}{dt} = - \sigma \, w(t-T) \tag{2} $$ について考えてみよう。 一般にこの種の微分方程式の解は振動的であって、長期的には$w(t) \lt 0$となる可能性もあるので、人口動態のモデルとして妥当であるためには、パラメータの範囲に制限が必要となる。
時間遅れがあるSEIRモデルの潜伏期間の分布
LambertのW関数を使うと $$ \lambda_1 = -\frac{W_0(-\sigma T)}{T} $$ $$ \lambda_2 = -\frac{W_{-1}(-\sigma T)}{T} $$
解の形を $w(t)= \exp(-\lambda t)$ とおいて、(2)式に代入すると、$\lambda$についての非線形方程式 $$ \lambda = \sigma \exp(\lambda T) $$ が得られる。 $\sigma$と$T$が適切な範囲にあれば($0\le \sigma T \lt 1/e$)、これは2つの異なる実数解(ここでは$\lambda_1, \lambda_2$とする)を持つことがわかり、 解は2つの指数関数の重ね合わせ $$ w(t) = A \exp(-\lambda_1 t) + B \exp(-\lambda_2 t) $$ で表せる。
$-T \le t \le 0$ で $w(t)=0$ という初期条件を課すと、$\frac{d w}{dt} = 0 \; (t \lt T)$ であるから $$ w(t) = C \; (0 \le t \lt T) $$ この定数 $C$ が E の数の初期値に対応し、EからI への遷移に伴って、(2)式に従ってその数が減少することになる。
解の連続性 $w(T) = C$ から $$ A \exp(-\lambda_1 T) + B \exp(-\lambda_2 T) = C $$
さらに、微分の初期条件 $w'(T)= -\sigma C$ を課すと $$ A \lambda_1 \exp(-\lambda_1 T) + B \lambda_2 \exp(-\lambda_2 T) = \sigma C $$
これらを解いて $$ A = \frac{C (\lambda_2 - \sigma) }{(\lambda_2 - \lambda_1) e^{-\lambda_1 T}}, \;\;\; B = \frac{C (\sigma - \lambda_1)}{(\lambda_2 - \lambda_1) e^{-\lambda_2 T}} $$
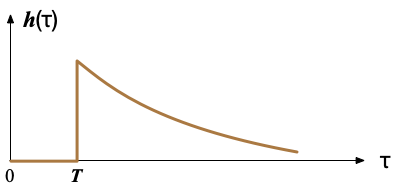
$h(t) = \left| \frac{d w(t)}{dt} \right| $ が潜伏期間の分布に対応するので、 分布関数を得る際には、規格化条件 $\int_0^\infty h(t) dt = 1$ より $C$ を決めればよい。
このとき、潜伏期間の分布関数$h(\tau)$は、以下のような概形となる(時間遅れ $T$ 以下では0、$T$ 以上では裾の広がりが異なる2つの指数関数の合成)。
以上のように、時間遅れを考慮したSEIRモデルの拡張版のひとつとして $$ \begin{eqnarray} \frac{dx(t)}{dt} & = & - \beta \, x(t) \, y(t) \\ \frac{dw(t)}{dt} & = & \beta \, x(t) \, y(t) - \sigma w(t-T) \\ \frac{dy(t)}{dt} & = & \sigma w(t-T) - \gamma y(t) \\ \frac{dz(t)}{dt} & = & \gamma y(t) \end{eqnarray} $$ が考えられる。 こうした遅延を取り入れた微分方程式を解くには、$T$だけ過去の値を初期条件として与える必要があるし、 数値的に扱う際は、現時点よりも$T$だけ以前までの各ステップの値を全て記憶しながら計算を進める必要がある。
潜伏期と発症している人数をまとめたモデル
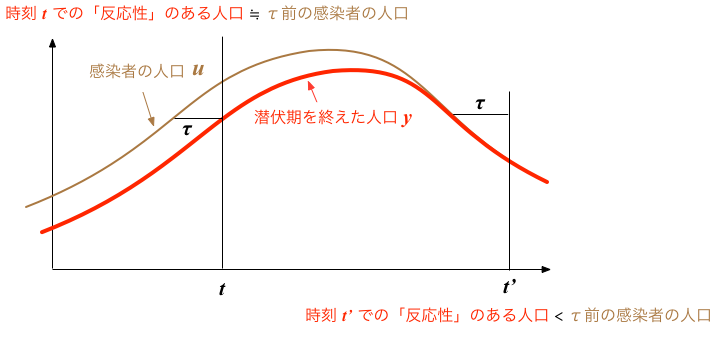
前節の、潜伏期の人数 $w(t)$ と発症者の人数 $y(t)$ を合算して、 $$ u(t) = w(t) + y(t) $$ と置き直してみると、 $$ \frac{du(t)}{dt} = \beta \, x(t) \, y(t) - \gamma y(t) $$ となる。 このままでは $x(t), u(t)$ だけで閉じた形にならないから、 罹患している者の総数 $u(t)$ の履歴から、発症者の数 $y(t)$ を与える関係を、畳み込み積分を使って $$ y(t) = \int_0^t u(t') \, g(t - t') \, d t' \tag{3} $$ と仮定(あるいは近似)してみよう。
ここで、$g(t) = \delta(t-T)$ と置いた場合、すなわち 時刻 $t$ での発症者人数が、ある時間 $T$ だけ以前の罹患者 $u(t-T)$ で近似できる $$ y(t) \approx u(t-T) \tag{4} $$ と考えると、 $$ \begin{eqnarray} \frac{dx(t)}{dt} & = & - \beta \, x(t) \, u(t-T) \\ \frac{du(t)}{dt} & = & \beta \, x(t) \, u(t-T) - \gamma \, u(t-T) \\ \frac{dz(t)}{dt} & = & \gamma \, u(t-T) \end{eqnarray} $$ のようなモデルも可能かもしれない。
または、患者の回復過程を I から R への変化として、ではなくて、EとIの全体 から R への緩和過程と捉えて $$ \begin{eqnarray} \frac{dx(t)}{dt} & = & - \beta \, x(t) \, u(t-T) \\ \frac{du(t)}{dt} & = & \beta \, x(t) \, u(t-T) - \gamma u(t) \\ \frac{dz(t)}{dt} & = & \gamma u(t) \end{eqnarray} $$ とする考えもあるかもしれない。 事実、後者は潜伏期を考慮したモデルとして、文献でも取り扱われている。
では、発症者数の見積もり ((4)式) は、どれくらい尤もらしいのだろうか。
感染の拡大期には、時刻$t$での感染者のうち、まだ潜伏期にあって、他者への感染に寄与しない人口が一定数あるはずである。 潜伏期間を$T$とすると、現在の感染者数$u(t)$の中で、すでに潜伏期間に達している者の見積もりとして $u(t-T)$ は妥当のように思われる。
その一方で、感染者数が定常的、あるいは減少傾向にある場合は、上記の見積もりは過大となる。 例えば、ある種の均衡が達成されて I の数が横ばいの場合でも、$u(t)$の中には一定の数の潜伏期にある人口が含まれるべきであるが、$u(t-T)$はそのことを反映しない。 さらに、感染が終息傾向にあって、潜伏期間にある者の比率が無視できるような状況では、さらに有効感染者を多く見積もり過ぎてしまうことになるだろう。 こうした観点からは、積分核 $g(t)$ をデルタ関数と置いてしまうような上記のモデリングは少なからず「乱暴」で、あまり素性が良くないように思われる。
 練習:時間遅れを含む常微分方程式
練習:時間遅れを含む常微分方程式
SIRモデルのコードを元にして、時間遅れのあるSEIRモデルを数値的に解くコードを作成してみなさい。
 ヒント
ヒント
時間遅れのある微分方程式 $$ \frac{dw(t)}{dt} = -\sigma \, w(t-T) $$ をオイラー法で計算するコードの例を以下に示す。 初期条件として $t \lt 0$ で $w(t)=0$ としている。 $\sigma \, T \gt 1/e$ の領域で解は振動的になる。
# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt
taxis=[ ]
waxis=[ ]
sigma = 0.05
T = 5
dt=0.001
nt = int(T/dt)
wmem = np.zeros((nt+1,))
w = 100
t = 0
cnt=0
while t<60:
wmem = np.roll(wmem,1)
wmem[0] = w
if cnt%100==0:
taxis.append(t)
waxis.append(w)
w = w - sigma * wmem[nt] * dt
t = t + dt
cnt = cnt + 1
plt.title("DELAY DE")
plt.plot(taxis,waxis, color=(1.0,0,0.0), linewidth=1.0, label='x')
plt.xlim(0,60)
plt.legend()
plt.xlabel('DAY')
plt.ylabel('W')
plt.grid(True)
plt.show()