Pythonプログラミング（ステップ５・多重ループ・整数の組み合わせ問題）
このページの目標
- 多重ループ構造を含むプログラムが、その変数の動きとともに、理解できる。
- 問題解決に向けてのアルゴリズムの選択、およびそれらの効率（計算量）について意識し、それらをプログラムに反映できること。
１．ピタゴラス数探し
いろいろな数（整数）の組み合わせの中から、ある条件にマッチしたものを見つけ出す、といった類の問題は多い。 「何の役に立つのだろう？ 」という疑問はさておいて、以下の課題にまず取り組んでみよう：
練習：ピタゴラス数探し
$a,b,c$ を正の整数としたとき $$ a^2 = b^2 + c^2 \tag{1} $$ を満たすような組$(a,b,c)$をピタゴラス数と呼ぶ。 $0< a,b,c < 100$ の範囲のピタゴラス数を探すプログラムを作成し、その範囲のピタゴラス数を全て列挙してみなさい。
ヒント
$n>2$の場合には$a^n = b^n + c^n$を満たす整数の組 a,b,c は存在しない、という有名なフェルマーの定理がワイルズによって証明されたのは（数学の歴史上は）つい最近のこと。これに触れている書籍なども多い（例えば、「数学ガール・フェルマーの最終定理」（結城浩・ソフトバンク））。 つまり、$n>2$の場合に、$(a,b,c)$の組を探そうとしても、それははじめから無理と「分かって」いる。 $n=2$の場合には、この等式を満たすような$(a,b,c)$が無限個存在することが証明でき、ピタゴラス数と呼ばれている。
ピタゴラスを探すもっとも素朴な方法は「a,b,cをそれぞれ1から100まで変化させてみて、実際に上の等式を満たすかどうかチェックし、もしそれを満たしたら画面のa,b,cの値をプリントする」というものだろう。そうすると、プログラムの骨格は
# coding: utf-8
for a in range (1,101,1):
for b in range (1,101,1):
for c in range (1,101,1):
if 等式が成り立つかどうか判定:
値をプリント
|
のようになるだろう。for文が「三重ループ」になっている点に注目。
ただし、この方法はあまり効率が良くない。高々100までの範囲でも100×100×100=100万回のチェックをしなければならない。 さらに大きなa,b,c にまで探索の範囲を拡大しようとすると、それなりの工夫が必要になるだろう。
効率化のためのアイデアとしては、例えば、
- 等式が成り立つ場合には、$a, b, c$ は直角三角形の辺の長さ（$a$が長辺）と解釈できるはず。すると、そもそも三角形を構成できないような$a,b,c$の組については調べる必要がないはずだ。
- $b,c$ がともに偶数であれば、$a$ はかならず偶数。$b,c$ がともに奇数の場合も $a$ は必ず偶数。つまり、これらの場合に奇数の $a$ を調べる必要はない。等々。
腕に覚えのある者は、$a,b,c$ が互いに素（最大公約数が1）であるような $a,b,c$ の組（原始ピタゴラス数）のみを出力するよう、プログラムを改造してみなさい。 最大公約数を計算するためのよく知られたアルゴリズムとして、ユークリッドの互除法がある。詳しくは、こちらのページや 情報基礎講義ノート（学内限定） を参照。
ヒント
円の方程式 $x^2 + y^2 = 1$ はパラメータ $t$ を使って $x(t)=\frac{1-t^2}{1+t^2},\ y(t)=\frac{2t}{1+t^2}$ と表示することができる。 この$t$は、左図のように、円を「串刺し」にする直線$y=t(x+1)$の傾きを意味している。
ここで、$t$ を有理数 $t=m/n$ （$n,m$は整数）と置けば、$x, y$ が有理数であるような組みを全て得られるはずである。 すなわち、有理数となるような$x, y$ は $x = \frac{n^2-m^2}{n^2+m^2}, \ y=\frac{2nm}{n^2 + m^2}$ で尽くされる。
一方、式 (1) を $\left( \frac{b}{a} \right)^2 + \left( \frac{c}{a} \right)^2 = 1$ と変形して、$x = \frac{b}{a}, \ y=\frac{c}{a}$ と考えれば、 上との対応から $a=n^2 + m^2, \ b = n^2 - m^2, \ c=2nm$ と表すことができる。 すなわち、２つの整数 $n,m$ についての組み合わせを与えれば、有理数であるような$t$が表す直角三角形と相似な三角形に対応したピタゴラス数を得ることができる。
発展練習：アームストロング数
$n$桁の10進数の各桁の$n$乗を加えると、その数に等しくなるような数（例えば $1^1=1$, $1^3 + 5^3 + 3^3 = 153$）はアームストロング数（ナルシスト数の一種）と呼ばれている。
10000までの範囲のアームストロング数を全て出力するプログラムを書きなさい。
ヒント
任意の $n$ 桁の10進数を $x$ とすると、$10^{n-1} \le x$ である。 一方、各桁を $n$ 乗した和 $y$ は $ n \times 9^n$ を超えることはない($y \le n \times 9^n$)。 ところが、べき乗関数の性質から、ある $N \lt n$ に対して必ず $ n \times 9^n \lt 10^{n-1}$ が成り立つような $N$ が存在するから、 $N$ よりも大きな $n$ については $y \lt x$、すなわち、各桁の $n$ 乗の和は、元の数よりも必ず小さくなる。 すなわち、$N$ より大きい桁のアームストロング数は存在しない。
$N$ の値を具体的に見積もるには、上記の不等式が成り立つようになる $n$ の値を1から順に調べてもよいし、 $n \times 9^n = 10^{n-1}$ の根から求めることもできる（その結果は、$N=60$ である）。
発展練習：四平方定理
ラグランジェの四平方定理によれば、全ての自然数 $n$ は、高々4つの自然数の平方の和で表すことができる。 つまり、任意の $n$ に対して $n = a^2 + b^2 + c^2 + d^2$ となるような非負の整数の組 $a, b, c, d$ が必ず存在する（そのうちのいくつかは0である場合を含む）。
$n$を入力すると、$(a, b, c, d)$の組を探索し、出力するプログラムを作成してみなさい。
2．線形整数計画問題
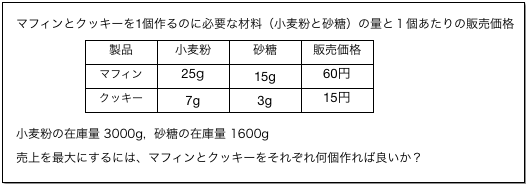
以下に、参考書の 3.8節『プラネタリウムカフェへようこそ』で、某高校の天文部に持ち上がった問題を示す：
ここで、作るマフィンの個数を$x$, クッキーの個数を$y$とする（もちろんどちらも整数）と、 売上額(円）は $$ 60 x + 15 y $$ となる。一方、小麦粉の使用量は$25 x + 7 y$ (g)、砂糖は$15 x + 3 y$ (g)となるが、いずれも在庫量を超えて使うことはできないから、 $$ \begin{eqnarray} 25 x + 7 y \le 3000 \\ 15 x + 3 y \le 1600 \end{eqnarray} $$ および、非負条件 $$ x \ge 0, \ \ y \ge 0 $$ が満たされていなければならない。 これは線形計画問題の一種で、特に、解が整数値に制限された 線形整数計画問題の例となっている。
一般の整数計画問題を効率的に解くアルゴリズムは知られていないので、最悪、「総当り」で 臨むしかない。 この例のように２変数の場合は、コンピュータを使えば、ほとんど瞬間的に解くことができるだろうが、 変数の数が増えると、可能な組み合わせが爆発的に増えてしまい、総当りは絶望的になる。 仮に、取り得る値が10通りしかなくても、10変数ならば、 $10^{10}$=100億通りの組み合わせとなってしまう。
練習：マフィンとクッキー問題
正の整数 $x, y$ の組み合わせを総当りで調べ、売上（作ったお菓子が売れ残ることは無いと仮定する）を最大にする個数の組とその時の売上金額を求めるプログラムを書いてみなさい。
ヒント
全ての非負の整数にわたって調べることは、無論、不可能なので、探索する範囲を限定する必要がある。 参考書 p.105-も参照に、探索の範囲をできるだけ絞り込むよう工夫すること。