Pythonプログラミング（ステップ８・関数・再帰処理）

６．関数の再起呼び出し

二つの整数$a,b$の最大公約数(greatest common divisor; gcd)を計算で求める方法を考えてみよう。 6と8だったら、すぐ2と判るけれども、494932553と162648336だったらどうなるだろう？ そこで、aとbを与えると、最大公約数を返すようなPythonの関数 gcd(a,b)を 設計してみたい。

アルゴリズム：ユークリッドの互除法

この問題の定番アルゴリズムは「ユークリッドの互除法」である。$a$と$b$（$a>b$)の最大公約数を$c$とすると、 互いに素な二つの数$\alpha$と$\beta$を使って $a = c \alpha$, $b=c \beta$と書き直すことができる。

このことを踏まえて、$a$を$b$で割った余りを$r$とすると、ある整数$n$を使って、 $$ a = n b + r $$ すなわち $$ c \alpha = n c \beta + r $$ となる。ここで$\alpha$と$\beta$は共通の因数を持たないのだから、$r$も$c$の倍数でなければならない。 つまり、ある整数$\gamma$を使って、$r = c \gamma$と書くことができる。 このとき、$\beta$と$\gamma$も互いに素でなければならない（そうでないと、共通因数をくくり出すことで、商$n$の値が変わってしまうから）。 以上の考察から、$a$と$b$の最大公約数は、$b$と$r$の最大公約数でもあることがわかった。

これを式で表すと$\gcd(a,b) = \gcd(b,r)$となる。このとき、常に$a>b>r$であることに注目しよう。 そして、$\gcd(b,r)$に対しても、同様の操作を繰り返す・・・・。 すると、いずれ$\gcd(c,0)$というパターンに到達するはずだ。

以上を踏まえると、以下のアルゴリズムで$a,b$の最大公約数を求めることができる：

1. a, bを与える
2. a = n*b + r となるような r を求める
3. r==0 ならば b が最大公約数 → 計算終了
4. (b,r)を(a,b)と読み替えて、2のステップから再び繰り返す

コーディング：再帰関数

これを、「素直に」Pythonの関数として表現すると、以下のようになるだろう：

gcd(a, b) {
  if (b==0):
     return a
  else:
     r = a%b
     return gcd(b,r)

この関数gcd()は、関数の定義の内部にgcd()自体が含まれる格好になっている。 このように、関数の計算の中にその関数の値が使われているような関数の定義のやり方を、関数の再帰的な定義、と呼ぶ。

このコードを使って、先ほどの大きな二つの数のgcdを出力するプログラムを書くと、以下のようになる（ rの計算を、関数の引数のところにまとめ、より簡潔に書き直した。結果は1であった）：

# coding: utf-8

def gcd(a, b):
  if (b==0):
     return a
  else:
     return gcd(b,a%b)


print(gcd(494932553,162648336))

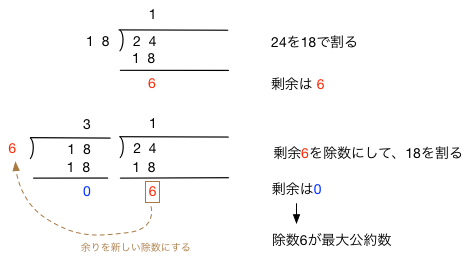
ここで、コンピュータの気持ちになって、gcd()関数がどのように計算を進めているのか、考えてみよう。 例えば、24と18の最大公約数を求めるプロセスを筆算で表すと

となる。これに対応して、gcd(24,18)は、 gcd()関数が全部で3回呼び出されて結果に至ることがわかる：

gcd(24,18)
    b(18) is NOT zero
     r←6 (24%18)
     RETURN gcd(18,6)
                b(6) is NOT zero
                 r←0 (18%6)
                 RETURN gcd(6,0)
                            b(0) is ZERO
                             RETURN 6

いちばん深いところで返された値 6 が、１つ上の gcd(6,0) の値となり、その値がさらに１つ上の gcd(18,6) の値になり、 そして、その値が gcd(24,18) の値となって return され、結果が確定する。

再帰を使うか、ループで表現するか

gcd(a,b)の関数定義の中で、gcd()が現れたのは、関数定義の末尾であった。 このようなパターンの再帰関数は、特に「末尾再帰」と呼ばれている。 末尾再帰の関数は、比較的簡単に、単純な繰り返しで書き直すことができることが知られている。 gcd()関数の場合は、例えば、以下のようにも表現でき、こちらのほうが計算は効率的である：

def gcd(a, b):
    while b!=0:
        r = a%b
        a = b
        b = r
    return a

こうしたケースを除けば、再帰を用いるとアルゴリズムを自然に表現できる場合が少なくないので、 是非、基本的なプログラミング手法のひとつとして、マスターしておきたい。

最後に、これまでに何度も登場した階乗計算を、再帰を使って表現したプログラム例を示す。

# coding: utf-8

def factorial(n):
    if n<=1:
       return 1
    else:
       return n*factorial(n-1)

# メイン部
print(factorial(10))

　練習：再帰を用いた総和計算

配列に入っているデータの総和を求める関数を、以下のアイデアに従って、設計しなさい。

• 配列に $n$個のデータ $a_i$ ($i=0, \cdots, n-1$)のデータが入っている。
• $j$番目から$k$番目までの要素の和を $\textrm{sum}(j,k)$ と書くと、配列の総和は $\textrm{sum}(0,n-1)$ と書ける。 また、$\textrm{sum}(j,j)=a_j$である。
• $j \le k < \ell$であるような数に対して $\textrm{sum}(j,\ell) = \textrm{sum}(j,k) + \textrm{sum}(k+1,\ell)$である。

# coding: utf-8

def sum(i,j,a):
    if i==j:
       return a[i]
    else:
    ....
    ....

# メイン部
a = [2,5,1,8,6,5,4]
print("SUM=",sum(0,len(a),a))

　ヒント

　練習：集合の要素の組み合わせ

こちらの練習問題に、再帰的な関数を使って取り組んでみなさい。

亀場で練習：フラクタル曲線

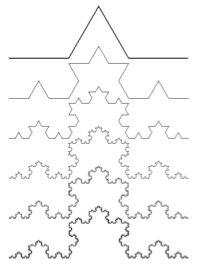
図のように、長さLの線分を、長さL/3の4本の線分で置き換える操作を考える。 置き換えられた線分にもまた同様の操作を繰り返すと、Koch曲線と呼ばれる（一見）複雑な曲線が得られる。 これは、フラクタル(fractal)な図形の例としてよく知られている。

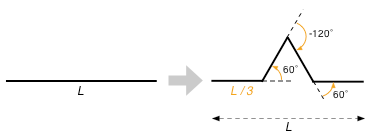
各線分に対して１回辺りに行う操作は下図のとおりである。この操作の再帰性に着目し、タートルグラフィックスを使って、Koch曲線を描くプログラムを作成しなさい。

　ヒント：

長さxの線分に対して、一回分の操作（折りたたみ）を施すということは、FD(x) ; という操作を

ttl.fd(x/3)
ttl.lt(60)  # 左に60°
ttl.fd(x/3)
ttl.rt(120) # 右に120°
ttl.fd(x/3)
ttl.lt(60)  # 左に60°
ttl.fd(x/3)

で置き換えることに他ならない。そしてまた、ttl.fd(x/3)の各部分に対して、同様の操作を繰り返せばよいはずだ。

操作はどこかで停止させなければならないから、折りたたまれた各線分の長さがある値（例えば1）よりも小さくなったら、 繰り返しを止めて、その部分は直線を描いて終了、とすればよい。

最初の線分の長さがxであるようなKoch曲線を描く関数をkoch(x)として、プログラムを完成させなさい。

from turtle3 import Turtle

def koch(x)
    if x<=1.0: 
    	ttl.fd(x)
    else:
       ??????
       ??????

# メイン部

ttl=Turtle("localhost")
ttl.clr()
ttl.rst()
ttl.pd()
koch(200)
ttl.pu()