Pythonプログラミング（ステップ４・反復処理・円周率の計算）

１．円周率の数値計算

円周率は、数学や自然科学・理工学のあらゆる領域に登場する、極めて重要な数であることは言うまでもなく、実際にそれを使った計算を行う機会が無くても、 $\pi \approx 3.14$ 程度の値であることは誰でも知っている。

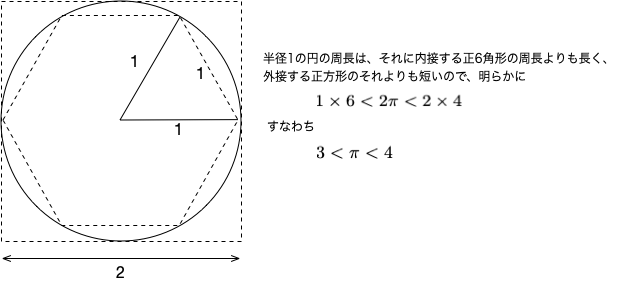
円周率は直径1の円の周長（半径1の円の周長の1/2）に他ならないから、円を多角形で近似した上で、正多角形の周の長さから見積もることができて、辺の数を増やすことで、近似の精度を上げることができる。 実際に、膨大な数の辺の正多角形を使った計算が続けられてきた。 こうした計算方法はとても手間がかかるため、一生をそれに費やした例さえもあったようである。

ニュートンの登場とともに、解析学的なアプローチによって、こうした計算は劇的に効率されることとなる。例えば、ニュートンは従来の計算方法を一新するような公式 $$ \pi = \frac{3 \sqrt{3}}{4} + 24 \left( \frac{2}{3 \cdot 2^3} - \frac{1}{5 \cdot 2^5} - \frac{1}{28 \cdot 2^7} - \frac{1}{72\cdot 2^9} - \frac{5}{704 \cdot 2^{11}} - \frac{7}{1664 \cdot 2^{13}} \cdots \right) $$ を得ている。

ニュートンがゲームチェンジャーとなって、その後は、円周率を効率的に計算する公式や手法が開発されるようになり、 現在(2021年8月）では、スーパーコンピュータを使って、62兆8000億桁まで計算されているようである。 また、民生品のパソコンを使って5兆桁の計算を行なった例もある（こちらを参照）。

効率的な計算方法のうちで、比較的むかしから知られていなものに、マチンの公式 $$ \pi = 16 \arctan\left(\frac{1}{5}\right) - 4 \arctan\left(\frac{1}{239}\right) $$ がある。 ここで、逆正接関数の近似値はテイラー級数 $$ \arctan(x) \approx \sum_{n=0}^M \frac{(-1)^n}{2n+1} x^{2n+1} $$ によって四則演算だけで求めることができる。

Pythonには、任意の精度で計算を行うことができるdecimalモジュールが標準で備わっているので、それを用いてマチンの公式によって円周率を1000桁計算するコードの例の以下に示す。

# coding: utf-8
from decimal import *

getcontext().prec = 1000

def arctan(x,N):
    s = Decimal(0)
    p = x
    for n in range(N):
        k = Decimal(2*n+1)
        if n%2==0:
            s = s + Decimal(1)/k * p
        else:
            s = s - Decimal(1)/k * p
        p = p * x * x
    return s

m = 250
pi = Decimal(16)*arctan(Decimal(1)/Decimal(5), 3*m+2) - Decimal(4)*arctan(Decimal(1)/Decimal(239), m)

print(pi)

　練習：検算

数値計算で求めた円周率の値が正しいかどうかを検算するためにはどのような方法があるか、考えてみなさい。

２．非効率な計算方法

以下では、Pythonプログラミングの演習の題材として、敢えて効率の悪い円周率の計算方法を試してみることにしよう。

方法１．ライプニッツの公式

円周率と関係する無限級数は多数知られているが、比較的古くから知られている公式のひとつにライプニッツの級数 $$ \frac{\pi}{4} = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} \cdots $$ がある。 これは、等式 $$ \arctan(1) = \frac{\pi}{4} $$ の左辺をテイラー級数で展開して得られる。

ニュートンの公式やマチンの公式とは違い、この交代級数はとても収束性が悪いことで知られている。

　練習： ライプニッツ級数

ライプニッツの公式に基づいて円周率を計算するコードを書いて、動作を確認してみなさい。

　ヒント

方法２．写像の反復回数

漸化式 $x_{n+1} = {x_n}^2 + c$ (ただし $x_0=0$）を考える。

$c \gt 1/4$ で $x_n$は最終的に発散するが、十分に小さな $\epsilon \gt 0$を考えて、$c = 1/4 + \epsilon$と置くと、 値が「爆発」するまでに一定の猶予期間が生じることとなる。

そこで、ある$\epsilon$に対して $x_n \lt 2$に留まっている状態で何回反復したかを $N(\epsilon)$で表すことにすると、 $$ N(\epsilon) \sqrt{\epsilon} \approx \pi $$ となることが示せる。

すなわち、0から出発して、値が2を超えるまで反復した「回数」に $\sqrt{\epsilon}$を乗じることで、円周率が得られる。

　練習： 漸化式の発散までの回数

上記の方法で実際に反復回数を計算し、それに基づいて$\pi$を見積もるPythonコードを書いてみなさい。

　ヒント

方法３．物体の衝突回数

高校で習った力学を思い出そう。ふたつの物体１と２が摩擦の無い床に置かれていて、x軸に沿って運動することができる。 $x=0$には壁があって、物体同士、そして物体と壁は完全弾性衝突（衝突の跳ね返り係数1）するとしよう。

ここで、物体1の質量を$m_1$, 速度を$v_1$と表記する。物体２についても同様に質量と速度を $m_2$, $v_2$ とする。

最初、物体２は静止しており($v_2=0$）、右側から物体１がそれに衝突する。そのときの速さを$V$とすれば、$v_1 = -V$である。

衝突される側（物体２）の質量が十分に小さければ（$m_2 \lt m_1$）、物体２は左側に弾き飛ばされ、壁に衝突する。そして、壁で向きが180度反転して、 再び物体１と衝突する。

このように「小さな」物体２は、物体１と壁の間を何回か往復運動する過程で、物体１は右向きの運動量を得て、運動の向きが反転し、物体同士の衝突も終了する。

速度 $v_1, v_2$の物体同士が衝突する際、衝突後の速度 $v'_1, v'_2$は、運動量保存とエネルギー保存の式 $$ \begin{eqnarray} m_1 v_1 + m_2 v_2 = m_1 v'_1 + m_2 v'_2 \\ \frac{1}{2} m_1 {v_1}^2 + \frac{1}{2} m_2 {v_2}^2 = \frac{1}{2} m_1 {v'_1}^2 + \frac{1}{2} m_2 {v'_2}^2 \end{eqnarray} $$ を連立させることで解くことができる。

また、物体２が壁に衝突すると、単純に速度の向きが反転する、すなわち $$ v'_2 = -v_2 $$ である。

$n$回目の衝突後の速度の組を$(v^{(n)}_1, v^{(n)}_2)$で表すことにすれば、以上の関係を使って、 $$ (-V, 0) \to \left(v^{(1)}_1, v^{(1)}_2 \right) \to \left(v^{(2)}_1, v^{(2)}_2 \right) \to \cdots $$ のように速度が変化し、最終的に $$ 0 \lt v_2 \lt v_1 $$ となった状態で、もはや衝突は生じなくなる。

物体２の質量が十分に小さな場合（$m_2 \ll m_1$）、物体２の衝突回数（物体１との衝突と壁との衝突の総数）を$N$とすると、驚くべきことに $$ N \sqrt{\frac{m_2}{m_1}} \approx \pi $$ すなわち、衝突回数をカウントして、質量比の平方根を乗ずると、円周率の近似値が得られる。

　練習： 衝突のシミュレーション

速度の変化を計算して衝突回数を見積り、円周率との関係性を確認してみなさい。

　ヒント

方法４．モンテカルロ法

モンテカルロ法を使って、半径1の二次元球（円）の面積（すなわち$\pi$)を求めることができる。 具体的な計算方法については、こちらのページを参照のこと。