暦と日付の計算（詳細編）

以下に進む前に、まず、 教材の暦と日付けについての基本編の内容を理解しておくこと。

基準日からの日数とその逆算

暦の基準（原点）となる日を、西暦0年3月1日に設定した場合、それから西暦 $y$ 年 $m$ 月 $d$ 日までの日数は、 $$ D(y,m,d) = 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor + \lfloor (153 m - 457)/5 \rfloor + (d-1) $$ と表すことができた。ただし、この式を使う場合、1月と2月の場合のみ、$m$ を（前年の）13, 14 と置かねばならなかった。

では、上記の基準日から $D$ 日だけ経過したら、それは何年何月何日にあたるのだろうか。 これは、例えば、「誕生日から1000日後は何月何日？」を知る際に必要となる計算である。

西暦0年から何年経過したか

基準日から $D$ 日経過した日は、何年目のサイクルにあたるかを求めるには、上記の日数を求める式が

2月末までの日数（きっちりy年分の日数） + 3月1日からの日数

という形をしていたことをまず思い出す。$D$ 日目は、$y$ 年目から $y+1$ 年目の間に無ければならないから、$y$ を求めるには不等式

$$ 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor \le D \lt 365 (y+1) + \lfloor (y+1)/4 \rfloor - \lfloor (y+1)/100 \rfloor + \lfloor (y+1)/400 \rfloor $$ を満たすような整数値 $y$ を探せば良い。 ここで、「切り捨て操作」について成り立つ関係 $$ \begin{eqnarray} -\lfloor x \rfloor = \lfloor -x \rfloor ,\\ x - 1 \lt \lfloor x \rfloor \le x \end{eqnarray} $$ を使うと、 $$ 365 y + y/4 - y/100 + y/400 - 3 \lt D \lt 365 (y+1) + (y+1)/4 - (y+1)/100 + (y+1)/400 $$ すなわち、$y$の必要条件として、 $$ {365.2425} y - 3 \lt D \lt {365.2425} {(y+1)} $$ が得られる。そうすると、$y$は、少なくとも、 $$ \frac{D}{365.2425} - 1 \lt y \lt \frac{D+3}{365.2425} $$ の範囲の整数であることがわかる。この不等式が与える$y$の範囲を考えると、この範囲にある整数はたかだか2つなので、 結局、以下のようにすれば$y$を一意に決めることができる：

(i) $y \leftarrow \lfloor \frac{D+3}{365.2425} \rfloor$ を仮の $y$ とおく

(ii) $y$が不等式(1)を満たす場合はその $y$、そうでなければ $y-1$ を改めて $y$ とおく

3月1日からの日数

こうして、基準日から $D$ 日目が、年数にして $y$ 年目にあたることがわかると、その年の3月1日からの日数（すなわち「残り」の日数）は $$ R = D - \left( 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor \right) $$ となる。 では、3月1日から $R$ 日目は何月何日になるのだろうか？

3月1日から各月のはじまりまでの日数を順に並べると、 $$ 0, 31, 61, 92, 122, 153, 184, 214, 245, 275, 306, 337 $$ となるから、対応する月を知るには、$R$ がどの区間に入っているかを調べればよいことになる。 例えば、$R=123$ ならば、$122 \le R \lt 153$ なので、7月、といった具合である。 $R$から月を換算する（効率の悪い）アルゴリズムを、Python風に書くと、以下のようになるだろう：

tab = [0, 31, 61, 92, 122, 153, 184, 214, 245, 275, 306, 337, 366]
i=0
while i<=11:
   if tab[i] <= R and R < tab[i+1]:
      break
   i=i+1
m=i+3

その日が何月かまでわかったら、 $$ S = D - \left( 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor + \lfloor (153 m - 457)/5 \rfloor \right) $$ が、その月のはじめから何日目かを表すことになる（$m$月1日の場合は $S=0$）。つまり、$d \leftarrow S+1$。

最後に、$m=13, 14$の場合のみ、$m=1, 2$ および $y \leftarrow y+1$ と読み替えれば、通常の日付けが得られる。

3月1日からの日数を返す関数の設計

これまでの説明で、各年の基点となる3月1日から$m$月1日までに日数を（怪しい式） $\lfloor (153 m - 457)/5 \rfloor$ とおいてきたが、 何故これで大丈夫なのだろうか。

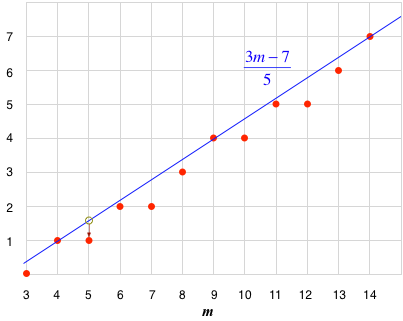
基点から日数の並びは $$ 0, 31, 61, 92, 122, 153, 184, 214, 245, 275, 306, 337 $$ であったが、1ヶ月の日数を30日+αと考えて（αは0か1）、αの部分だけの増分を見ると、この数値の列は $$ 0, 1, 1, 2, 2, 3, 4, 4, 5, 5, 6, 7 $$ となる。$m$ との対応が分かりやすいようグラフに描くと以下のとおりである（赤丸がデータ点）。

ここで直線 $(3m-7)/5$ を引くと、$m=4, 9, 14$ の値はぴったりデータ点を通り、それ以外の点は、全て直線の下側に位置することがわかる。 しかも、直線と赤丸は、縦方向に1以上は離れていない。 つまり、$(3m-7)/5$ の小数点以下を切り捨てると（つまり $\lfloor (3m-7)/5 \rfloor$ は）、どの月でも赤丸の値に一致する（たとえば、グラフの $m=5$ のところを参照）。

上の議論は、各月の30日からの「お釣り」についてのものだったから、3月1日からの日数は $$ \lfloor (3m-7)/5 \rfloor + 30 (m-3) $$ となるが、あとから加えた分は整数なので（小数点以下を持たないので）、「切り捨て」の中に入れてしまっても、結果に影響しない。 式を整理すると $$ \lfloor (153m-457)/5 \rfloor $$ が得られる。

上記はひとつの例に過ぎず、たとえば、赤点の下側すれすれを通る直線を引いて、その値を切り上げることでも、別バージョンの関数がすぐ作れそうだ。 $m=0, \cdots, 14$ の範囲に限れば、同じ結果が得られる式のパターンは他にも沢山あるに違いない。 例えば、日本語版のWikipediaには $$ \left\lfloor \frac{306 (m+1)}{10} \right\rfloor - 122 $$ という式が紹介されている。

別のアイデア