Pythonプログラミング（その他のトピック・チューリングパターン）

アラン・チューリングの予見

インクを紙や布に上に垂らすと、乾燥してしまわないうちは、そのシミはじわじわと周りに広がってゆく。 位置 $x$、時刻 $t$ でのインクの濃度を $u(x,t)$ とすると、このような過程は拡散方程式 $$ \require{physics} \frac{\partial u(x,t)}{\partial t} = \laplacian u(x,t) $$ で表現される。 ここで、右辺のラプラス演算子 $ \laplacian = \nabla \cdot \grad $ は、二次元デカルト座標の場合は $$ \laplacian = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} $$ のように比較的簡単な形をしているが、座標系が変わると、その座標系での勾配と発散から求める必要があって、案外と複雑な 形になることは、数学の授業で学んだとおりである。

インクに限らず、物質の拡散は「ボヤケながら広がる」性質を持つのであって、広がったインクが一点に集まってくるようなことは無い。

このことは生物でも同様で、細胞や組織の中の様々な化学物質は、ミクロなスケールでは、拡散によって受動的に輸送されている （それだけでは機能的に不十分な箇所では、細胞レベルでミオシンモーターやイオンポンプ等の能動的な輸送が行われているし、長距離の輸送のために 循環器が発達するわけであるが、ここではその中間的な空間スケールでの現象を想定することにする。）

多細胞生物では、すべての細胞が同じ遺伝情報を持つにもかかわらず、様々に分化しながら、全体としての形や機能が維持されている。 そうすると、発生の過程でそれぞれの細胞は自分がどのように分化すべきかの情報を、何らかのやり方で知る必要がある。 生命は様々な化学物質とそれらの複雑な反応を通じて維持されていることを考えると、そうした化学物質の濃度や勾配を介して位置情報が 細胞に伝えられているのではないか、と考えるのは自然であろう。

ところが、化学物質の輸送が拡散によるとすれば、物質濃度は本来的に一様になろうとするはずで、 自発的にある物質の濃度が高い場所が生成されるとは考えにくい。

そこに、数学や計算機科学の分野でよく知られるアラン・チューリングは、新しいシナリオを提案した(1952)。 彼は、二種（以上）の化学物質が反応を伴いながら拡散することで、濃度の不均一（濃度の波）が自発的に生じることを数学的な解析によって明らかにしたのである。 当初、このチューリングのアイデアは数学的なモデルに過ぎず、実際の生物現象の説明には使えないだろうと思われていたが、 論文発表から半世紀ほどを経て、魚の体表の模様を使った実験によって、チューリングのモデルにより現象を定量的に予見できることが実証されている。

さらに詳しくは、この分野の第一人者である近藤滋先生の講演『キリンの模様がつなぐ物理学と生物学』も参照のこと。

生物の形態形成の反応拡散モデル

チューリングの提案したモデルは、反応拡散方程式と呼ばれ一組の偏微分方程式の一種で、 ２種の物質が関係する場合、空間と時間に依存する変数 $u(x,t)$, $v(x,t)$ が、 $$ \begin{eqnarray} \frac{\partial u}{\partial t} & = & D_u \laplacian u + f(u,v) \\ \frac{\partial v}{\partial t} & = & D_v \laplacian v + g(u,v) \end{eqnarray} $$ によって時間発展する。 ここで、$f(u,v)$, $g(u,v)$ は反応速度を表す一般には非線形な関数を表し、 $D_u$および$D_v$がそれぞれの物質の拡散定数である。 ここで、拡散定数と反応速度を適切に選ぶと、$u$や$v$が空間的に非一様に自己発展するような場合があることを、 チューリングは理論的に示したのである。

この種のモデルには、変数の数や非線形関数、界条件によって、様々なバリエーションが存在するが、 ここではその一例として、ゼブラフィッシュの体表のパターンの研究( Yamaguchi et al., PNAS(2007)) で使われているモデル $$ \begin{eqnarray} \frac{\partial u}{\partial t} & = & D_u \laplacian u + a - bu + \frac{u^2}{v(1+cu^2)} \tag{1}\\ \frac{\partial v}{\partial t} & = & D_v \laplacian v + u^2 - v \tag{2} \end{eqnarray} $$ をPythonを使って数値シミュレーションしてみよう。 化学反応速度を与える関数は、この場合、$f(u,v) = a - bu + \frac{u^2}{v(1+cu^2)}$, $g(u,v) = u^2 - v$ ということになる。 ここで、$a, b, c$はパラメータ（数値）である。

また、体表のモデルということで空間は二次元とするので、具体的には$u=u(x,y,t)$、$v=v(x,y,t)$の時間・空間発展を調べることになる。

フーリエ変換を使ったラプラス演算子の計算

反応拡散方程式のシミュレーションを行うには、ラプラシアンを計算する必要がある。 ラプラシアン等の微分を数値的に計算するには差分近似を用いることも多いが、ここで、離散フーリエ変換を使った方法について考えてみよう。

まずは簡単のため、一次元の周期境界の系を考え、$N$個の等間隔に並んだ点の上の、$\ell$番目の値を $u_\ell$ と置くことにしよう （以下では$u_\ell$が実数の場合のみを考える）。 そのようなデータを離散フーリエ変換 $$ U_k = \sum_{\ell} u_\ell \exp\left( - \frac{2 \pi k \ell}{N} i \right) $$ したデータセット $\{ U_k \}$ が与えられると、元のデータは、その逆変換 $$ u_\ell = \frac{1}{N} \sum_{k} U_k \exp\left( \frac{2 \pi k \ell}{N} i \right) \tag{3} $$ によって再構成できる。

上式は、$u_\ell$の値というのは、格子間隔を単位として、周期が2から最大周期が$N$までの複数の「波」の重ね合わせとして表現できる ことを意味しており、フーリエ空間では$k=1$が周期$N$の、そして$k=N/2$が周期2の波（振動）のモードに対応している。 このことは、$k \ge N/2$ の振動モードは、$k' = 1,2,\cdots,N/2-1$ として $$ \begin{eqnarray} \exp\left(2\pi i (N-k') \ell \big/ N \right) & = & \exp\left(- 2\pi i k' \ell \big/ N \right) \exp\left(2\pi i \ell \right) \\ & = & \exp\left(- 2\pi i k' \ell \big/ N \right) \end{eqnarray} $$ のような波が「折り返された」ものとして扱う必要があることを意味している。

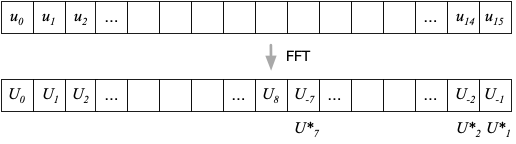
以上を踏まえ、式(3)の和の前半と後半に分けてた上で、後半を「折り返した」かたちに書き直すと $$ \begin{eqnarray} u_\ell &=& \frac{1}{N} \sum_{k=0}^{N/2} U_k \exp\left( \frac{2 \pi k \ell}{N} i \right) + \frac{1}{N} \sum_{k'=1}^{N/2-1} U_{N-k'} \exp\left( \frac{-2 \pi k' \ell}{N} i \right) \end{eqnarray} $$ となる。 NumPyなどの計算ライブラリの離散フーリエ変換では、配列の前半部分に $U_k$に相当する部分が、 そして配列の後半部分に$U_{N-k'}$に相当する部分が格納されている。 さらに、$U_{N-k} = U^*_k$が一般に成り立つので、例えば配列の最後の要素は、$U_1$の複素共役が格納されていることになる。

次に、$\ell$を座標(すなわち$x=\ell$)と考え、上式の$u$の$\ell$について微分を取ると $$ \begin{eqnarray} \frac{\partial u_\ell}{\partial \ell} & = & \frac{1}{N} \sum_{k=0}^{N/2} \left[ \frac{2\pi k}{N} i \right] U_k \exp\left( \frac{2 \pi k \ell}{N} i \right) \\ &+& \frac{1}{N} \sum_{k'=1}^{N/2-1} \left[ - \frac{2\pi k'}{N} i \right] U_{N-k'} \exp\left( -\frac{2 \pi k' \ell}{N} i \right) \end{eqnarray} $$ となる。

同様に、二階微分（ラプラシアン）は $$ \begin{eqnarray} \frac{\partial^2 u_\ell}{\partial \ell^2} & = & \frac{1}{N} \sum_{k=0}^{N/2} \left[ - \left( \frac{2\pi k}{N} \right)^2 \right] U_k \exp\left( \frac{2 \pi k \ell}{N} i \right) \\ &+& \frac{1}{N} \sum_{k'=1}^{N/2-1} \left[ - \left( \frac{2\pi k'}{N} \right)^2 \right] U_{N-k'} \exp\left( -\frac{2 \pi k' \ell}{N} i \right) \end{eqnarray} $$ となる。 すなわち、$k$番目のフーリエ成分 $U_k$ には因子 $- \left( \frac{2\pi k}{N} \right)^2$ を、 $U_{N-k'}$ には因子 $- \left( \frac{2\pi k'}{N} \right)^2$ を乗じた上で 逆変換することで、$\ell$番目のデータ点のラプラシアンが求まるわけである。

上記は、データが$N$毎に周期的に配置されていること（すなわち周期境界条件）が前提であるので、境界条件が異なる場合は別途工夫が必要となる。

同様に、二次元の場合も、矩形の格子状に等間隔に並んだデータ点 $(x,y)$を考えると（ただし、$x$方向に$N$点、$y$方向には$M$とする）、 離散フーリエ変換 $$ U_{pq} = \sum_x \sum_y u_{xy} \exp\left( - \frac{2 \pi p x}{N} i - \frac{2 \pi q y}{M} i \right) $$ の逆変換は $$ u_{xy} = \frac{1}{NM} \sum_p \sum_q U_{pq} \exp\left( \frac{2 \pi p x}{N} i + \frac{2 \pi q y}{M} i \right) $$ となるから、それを使うと、ラプラシアンは同様に $$ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \frac{1}{NM} \sum_p \sum_q \left[ - \left( \frac{2\pi p}{N} \right)^2 - \left( \frac{2\pi q}{M} \right)^2 \right] U_{pq} \exp\left( \frac{2 \pi p x}{N} i + \frac{2 \pi q y}{M} i \right) $$ で評価できる。 すなわち、この場合、各フーリエ成分に因子 $- \left( \frac{2\pi p}{N} \right)^2 - \left( \frac{2\pi q}{M} \right)^2$ を乗じて、逆変換すればよい。 ここでは式が煩雑になるため、折り返しについては省いたが、1次元と同様に、x方向には$N/2 \lt x$, y方向には$M/2 \lt y$で処理を分ける必要がある。

上記のようなフーリエ変換を用いた方法は手間がかかる一方で、１点の微分の評価に全てのフーリエ成分（周期関数）の寄与まで考慮されることから、差分を用いる方法に比べて著しく誤差が小さくなることが知られており、その性質は spectral accuracy などと呼ばれている。

シミュレーションコード

では、具体的に、(1), (2)式のモデルをシミュレーションするコードを書いてみよう。

二次元空間をNumPyの二次元配列で表現すると、NumPyのブロードキャスト機能によって、要素毎の計算を陽に書かなくても済ませることができる。 また、前節のとおり、配列を離散フーリエ変換して適切な係数を乗じた上で逆変換することで、全ての点のラプラシアンを求めることができる

これらを踏まえてコーディングした例を以下に示す。このコードは、時間発展の様子を可視化するため、アニメーション表示するようにしている。

ここで、prep_laplacian_op(n,m)は、ラプラス変換の際に必要な各係数を予め求めておいて再利用するための関数で、 関数laplacian(a, op)は、一旦求めた係数配列opを使って、二次元配列のラプラス変換を返す。 データ点数を$N$とするとき、ラプラシアンを求めるためにフーリエ変換された配列の$k$番目の要素に掛け合わせるべき係数は、 $k \le N/2$では$-\left(\frac{2\pi k}{N}\right)^2$、 $k \gt N/2$では$-\left(\frac{2\pi (k-N)}{N}\right)^2$ であることに注意。

変数の時間発展を計算しているのは、関数redraw()の中の

for cnt in range(100):
  dudt = D_u * laplacian(u,op) + p_a - p_b*u + u*u/(v*(1.0+p_c*u*u))
  dvdt = D_v * laplacian(v,op) + u*u - v
  u = u + dudt*dt
  v = v + dvdt*dt
  t = t + dt

の部分で、オイラーの前進差分を用いている。 forループで100回繰り返しているのは、反復の都度描画すると変化が感じられないため、100回の更新毎に表示するようにしているためである。

# coding: utf-8

import numpy as np
import random
import math
import pyglet
from pyglet.gl import *

def prep_laplacian_op(n,m):
    A = np.zeros((n,m))
    for p in range(0,n):
        xi = 2*math.pi*p/n if p<=n//2 else 2*math.pi*(p-n)/n
        for q in range(0,m):
            eta = 2*math.pi*q/m if q<=m//2 else 2*math.pi*(q-m)/m
            A[p,q] = -xi*xi-eta*eta
    return A
            
def laplacian(a, op):
    a2 = np.fft.fft2(a)
    a2 = op * a2
    return np.fft.ifft2(a2).real

###

N = 128

p_a = 0.0
p_b = 1.2
p_c = 0.4

D_u = 0.2
D_v = 4.0

t = 0
dt = 0.001

op = prep_laplacian_op(N,N)

u = np.random.uniform(low=0.0, high=1.0, size=(N,N))
v = np.random.uniform(low=0.0, high=1.0, size=(N,N))

SCALE = 4
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
win.set_caption('Fish Skin Pattern')

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0,1)
    for i in range(N):
        for j in range(N):
            col = u[i,j]
            r = 0.4 + (1 + math.cos(math.pi*col))*0.25
            g = 0.4 + (1 + math.cos(math.pi*col*0.125))*0.25
            b = 0.5 + (1 + math.sin(math.pi*col*0.3333333333333333))*0.25
            glColor3d(r,g,b)
            glBegin(GL_POLYGON)
            glVertex2d((i+0)*SCALE,(j+0)*SCALE)
            glVertex2d((i+1)*SCALE,(j+0)*SCALE)
            glVertex2d((i+1)*SCALE,(j+1)*SCALE)
            glVertex2d((i+0)*SCALE,(j+1)*SCALE)
            glEnd()

    str = 'T={0:.3f}'.format(t)
    label = pyglet.text.Label(str,
                              font_name='Helvetica', color=(255,255,255,255),
                              font_size=12, x=10, y=10)
    label.draw()

def update(deltat):
    global u,v,t
    for cnt in range(100):
        dudt = D_u * laplacian(u,op) + p_a - p_b*u + u*u/(v*(1.0+p_c*u*u))
        dvdt = D_v * laplacian(v,op) + u*u - v
        u = u + dudt*dt
        v = v + dvdt*dt
        t = t + dt

pyglet.clock.schedule_interval(update, 1/20.0)
pyglet.app.run()

上記のコードを実行すると、パソコンによっては時間がかかるかもしれないが、ランダムな初期条件から、 以下のようなパターンが徐々に浮かびかがってくるはずである。 スーパーの鮮魚コーナーを歩いていると、真さばの背中の表面は、ちょうどこんな感じのパターンになっている。

写真は Honda釣り倶楽部 へのリンク

Google Colaboratory用のコード

Google Colabのノートブック上では上記のpygletを使用したコードは動作しないため、 代わりにmatplotlibの機能でアニメーション表示する例を記載しておく。

import numpy as np
import random
import math
import matplotlib.pyplot as plt
from matplotlib import animation, rc, cm

def prep_laplacian_op(n,m):
    A = np.zeros((n,m))
    for p in range(0,n):
        xi = 2*math.pi*p/n if p<=n//2 else 2*math.pi*(p-n)/n
        for q in range(0,m):
            eta = 2*math.pi*q/m if q<=m//2 else 2*math.pi*(q-m)/m
            A[p,q] = -xi*xi-eta*eta
    return A
            
def laplacian(a, op):
    a2 = np.fft.fft2(a)
    a2 = op * a2
    return np.fft.ifft2(a2).real

###

N = 128

p_a = 0.0
p_b = 1.2
p_c = 0.4

D_u = 0.2
D_v = 4.0

op = prep_laplacian_op(N,N)

u = np.random.uniform(low=0.0, high=1.0, size=(N,N))
v = np.random.uniform(low=0.0, high=1.0, size=(N,N))
t = 0
dt = 0.005

def nextstep():
    global u,v,t
    for cnt in range(100):
        dudt = D_u * laplacian(u,op) + p_a - p_b*u + u*u/(v*(1.0+p_c*u*u))
        dvdt = D_v * laplacian(v,op) + u*u - v
        u = u + dudt*dt
        v = v + dvdt*dt
        t = t + dt

fig = plt.figure()
images = []
while t<10.0:
    img = plt.imshow(u,cmap="summer")
    images.append([img])
    nextstep()

anim = animation.ArtistAnimation(fig, images, interval=200)
rc('animation', html='jshtml')
plt.close()
anim

　練習：時間方向の差分スキームの改良

上のサンプルコードでは、時間方向にはオイラーの前進差分を用いている。ルンゲクッタ法等を使ってさらに精度を高める工夫を施してみなさい。

　練習： Gray-Scott モデル

Gray-Scottモデルと呼ばれる反応拡散方程式 $$ \begin{eqnarray} \frac{\partial u}{\partial t} & = & D_u \laplacian u - u v^2 + a(1-u) \\ \frac{\partial v}{\partial t} & = & D_v \laplacian v + u v^2 - v(a+b) \end{eqnarray} $$ について、同様にシミュレーションしてみなさい。

パラメータとしては、 $D_u=0.2, D_v = 0.1, a=0.02, b=0.05$ でまず試してみると良い。 また、初期条件として、$u$を全体に分布させた上で、$v$の濃度が高いスポットを設けてみること。

　練習： Cahn-Hilliard 方程式

チューリングパターンとは全く異なる機構で「縞模様」が生じる数理モデルとして、 合金や高分子ブレンド系の相分離を理想化したCahn-Hilliard方程式が知られている。 $c(x,y,t)$を、座標$(x,y)$ 時刻$t$での秩序変数（仮にA, Bの２つの相が存在する場合、$c=1$がA相、$c=-1$がB相を表すような量）とすると、その時間発展は 偏微分方程式 $$ \frac{\partial c}{\partial t} = \nabla^2 \left(c^3 - c \right) - \gamma \nabla^4 c $$ によって記述される。

$c=0$に近いランダムな初期状態から出発して、$c$がどのように時間発展するか、チューリングパターンの計算方法に倣って、その様子をシミュレーションしてみなさい。

　ヒント

$\nabla^4$は重調和演算を表し、二次元デカルト座標の場合は $$ \nabla^4 c = \frac{\partial^4 c}{\partial x^4} + 2 \frac{\partial^4 c}{\partial x^2 \partial y^2} + \frac{\partial^4 c}{\partial y^4} $$ である。これをフーリエ変換によって計算するには、各フーリエ因子に $$ \left( \frac{2\pi p}{N} \right)^4 + 2 \left( \frac{2\pi p}{N} \right)^2 \left( \frac{2\pi q}{M} \right)^2 + \left( \frac{2\pi q}{M} \right)^4 $$ を乗じてから逆変換すれば良い。

（書きかけ）