Pythonプログラミング（鞍点法）

このページでは、複素解析の授業で登場する鞍点法の様子をPythonを使って観察する（このページはこれから）。

１．階乗関数とスターリングの公式

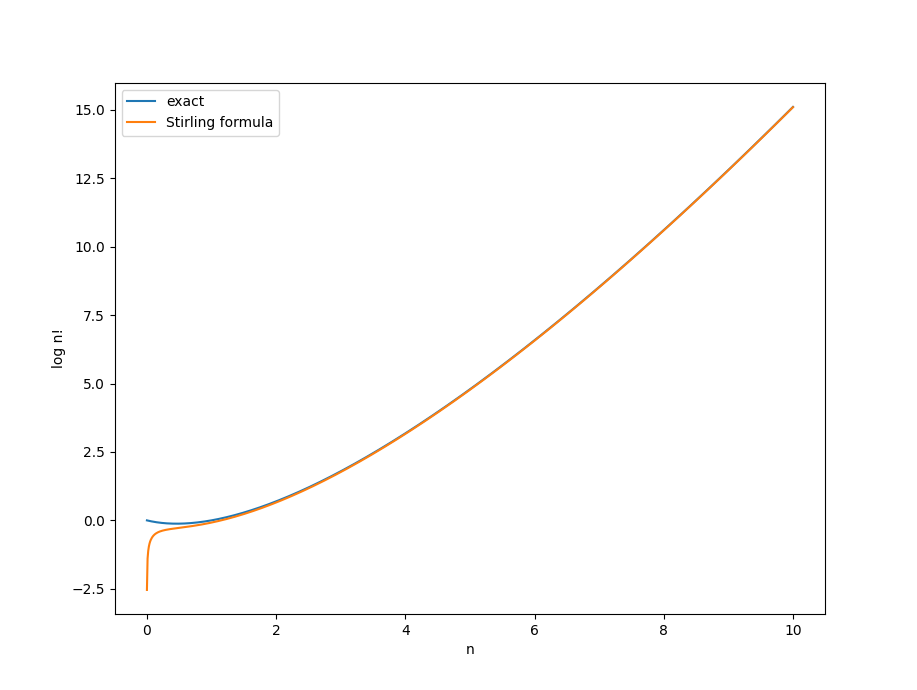
ガンマ関数、あるいは階乗の値をよく近似する式として、スターリングの公式がよく知られている。 $n$の階乗は、ガンマ関数を使うと $$ n ! = \Gamma(n+1) $$ であることを思い出し、どれくらい「良い」近似になっているのかを確かめてみよう。 階乗が急激に増大することから、その値の対数値 $\log \Gamma(n+1)$と、スターリングの公式が与える $$ \log(n!) \approx \left(n+\frac{1}{2}\right) \log n - n + \frac{1}{2}\log(2 \pi) $$ とを比較してプロットしてみたのが以下のコードとグラフである：

# coding: utf-8
import numpy as np
from scipy.special import gamma
import matplotlib.pyplot as plt

n = np.linspace(0.001, 10, 1000)

log_gamma = np.log(gamma(n+1))
log_stirling = (n+0.5)*np.log(n) - n + 0.5*np.log(2*np.pi)

plt.plot(n,log_gamma,label='exact')
plt.plot(n,log_stirling,label='Stirling formula')
plt.xlabel('n')
plt.ylabel('log n!')
plt.legend()
plt.show()

グラフからも読み取れるように、比較的小さな$n$に対しても、２つの曲線はピタリと一致しており、極めて良い近似が得られていることが分かる。

このスターリングの公式は、鞍点法と呼ばれる方法で導出できるのだが、それはどのようなカラクリなのだろうか。

２．鞍点法

ガンマ関数は $$ \Gamma(z+1) = \int_0^{\infty} t^z e^{-t} dt $$ のように定義される（階乗の定義と合わせるため、$\Gamma(z)$ではなく$\Gamma(z+1)$を考えることにする）。

ここで、天下り的ではあるが、$z$を絶対値と偏角に分け、$z = |z| e^{i \alpha}$と置いた上で 積分を $$ \int_a^b e^{|z| \, h(s)} ds \tag{1} $$ のような形になるように変形してみる。 具体的には、$t = z (s+1)$と変数変換すると $$ \Gamma(z+1) = z^{z+1} e^{-z} \int_{-1}^{\infty} e^{|z|\,e^{i \alpha} \left(\log(s+1) - s \right)} ds $$ とできるので $$ h(s) = e^{i \alpha} \left(\log(s+1) - s \right) $$ と見なせば、確かに式1の形になっている。すなわち、 $$ I(z) = \int_{-1}^{\infty} e^{|z|\,h(s)} ds $$ がどのように$z$に依存するかが評価できれば、ガンマ関数の値も評価できることになる。 ここで、一般に$s$は複素数で、積分路は$-1$から$+\infty$まで実軸に沿って取ることになるが、 複素関数論の教えるところによれば、被積分関数が正則な領域では始点と終点さえ同じにしておけば、途中の積分路を変更しても結果は変わらない。

ここで、$h(s)$を実部$u(s)$と虚部$v(s)$に分けて $$ h(s) = u(s) + i v(s) $$ と置くと、被積分関数の絶対値は $$ \left| e^{|z| h(s)} \right| = e^{|z| u(s)} $$ となるから、積分経路のうちでこれが大きい「場所」が積分全体への寄与が大きいことになる。 そうすると、これが最大値を取る場所を探したくなるが、最大絶対値の原理(maximum modulus principle)から、 ある領域を設定しても、その領域の内部に最大値（同様に最小値も）を取るような点は存在しない。

その一方で、$|z| h(s)$の微分が0となるような点$s_0$は存在して、 $$ |z| \frac{d h(s)}{ds} = |z| \left( \frac{1}{1+s} -1 \right) = 0 $$ から$s_0=0$であることが分かる。 $e^{|z| u(s)}$が最大値と最小値のいずれも取らないことから、$s_0$は $|z| u(s)$の鞍点(saddle point)となっていることがわかる （指数関数の性質から、$s_0$は $e^{|z| u(s)}$ の鞍点でもある）。

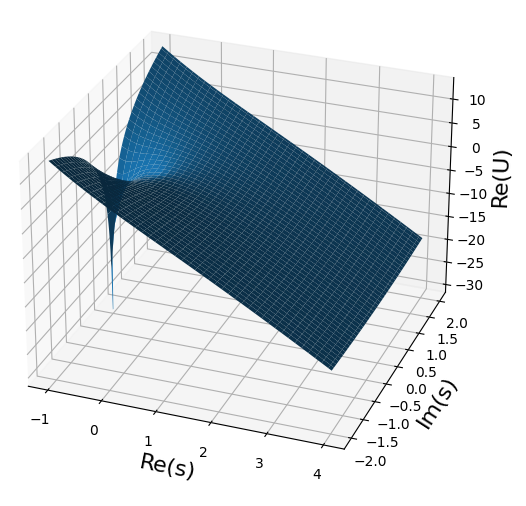
$u(s)$の鞍点の周りの様子を観察するPythonコードの例を以下に示す。

# coding: utf-8                                                                                                                        
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

z_abs = 8
alpha = 0 # radian                                                                                                                     

z = z_abs * (np.cos(alpha) + np.sin(alpha)*(0+1j))

x = np.linspace(-1, 4, 256)
y = np.linspace(-2, 2, 256)
X, Y = np.meshgrid(x, y)
S = X + Y * (0+1j)
H = z * (np.log(1 + S) - S)

U = np.real(H)
V = np.imag(H)

fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111, projection="3d")
ax.set_xlabel("Re(s)", size = 16)
ax.set_ylabel("Im(s)", size = 16)
ax.set_zlabel("Re(U)", size = 16)
ax.plot_surface(X, Y, U)
plt.show()

この例では$\alpha=0$とした。確かに$s=0$が鞍点になっていることと、鞍点を通る切り通しのような経路（最急降下の道）が存在することが確認できる。

他方で、虚部の$|z| v(s)$のほうは、鞍点の周りで最急降下の道に沿って一定値となる（上記のコードを修正して確かめてみよ）。

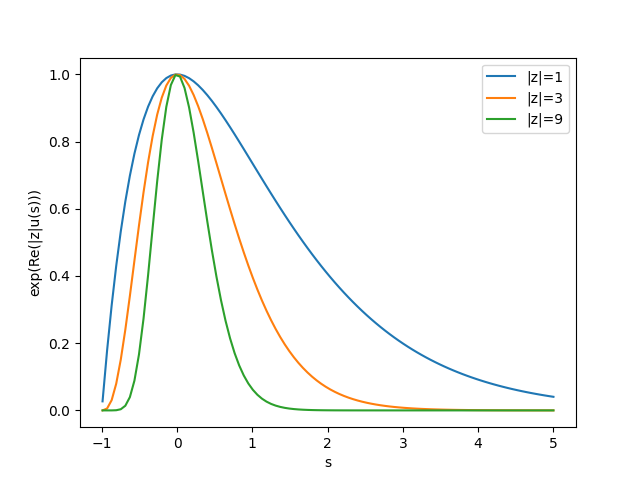
積分路をこの最急降下の道を通るようにして、$|z|$を大きくすると、$e^{|z| u(s)}$ はガウス型の関数形に近づいていく。 簡単のため$\alpha=0$とすると、最急降下の道は実軸に沿った経路となるが、そのときの$e^{|z| u(s)}$の様子を $|z|$を変えながらプロットしてみると以下のようになる。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt

s = np.linspace(-1+0.01, 5, 100)

u1 = np.exp(np.log(1+s) - s)
u3 = np.exp(3*(np.log(1+s) - s))
u9 = np.exp(9*(np.log(1+s) - s))

plt.plot(s,u1,label='|z|=1')
plt.plot(s,u3,label='|z|=3')
plt.plot(s,u9,label='|z|=9')
plt.xlabel('s')
plt.ylabel('exp(Re(|z|u(s)))')
plt.legend()
plt.show()

$|z|$を大きくすると、関数がガウス型に近づくだけでなく、幅も狭まることから、 積分全体の値は鞍点のごく近傍だけの様子に支配されるであろうことも同時に見て取れる。

計算の詳細は専門書を確認していただくこととし、結果だけを示すと、$|z| \gg 1$で $$ \int e^{|z| h(s)} ds \sim e^{|z| h(s_0)} \left( \frac{2\pi}{a |z|} \right)^{1/2} e^{\frac{\pi - \phi}{2} i} \tag{2} $$ となる。 ここで、$a$と$\phi$は$h(s)$の二階微分の鞍点での絶対値と偏角で、 $$ h''(s_0) = a e^{i \phi} $$ である。 式2の中の1/2乗の箇所が、無限区間のガウス積分に由来することはすぐに想像できるだろう。 また、$\frac{\pi - \phi}{2}$は、最急降下の道の方向（偏角）を表している。

今考えている$h(s)=e^{i \alpha} ( \log(1+s) - s )$については $$ h''(0) = e^{(\alpha+\pi) i} $$ すなわち$a=1$, $\phi = \alpha + \pi$である。

以上をまとめた結果、ガンマ関数の漸近形(asymptotic form)、すなわちスターリングの公式 $$ \Gamma(z+1) \sim z^{z+1} e^{-z} \left( \frac{2\pi}{z} \right)^{1/2} $$ が得られる。 この近似式の精度が恐ろしく良いのは、$|z|$がそれほど大きく無い場合でも、式1の積分が鞍点の近傍でガウス積分に極めて近い格好になっているからである。

　練習：鞍点の様子の観察

1. 鞍点の周りで$h(s)$の実部$u(s)$の様子を表示するコードの例を元にして、虚部$v(s)$の様子も観察してみなさい。
2. 同様に、$z$の偏角$\alpha$が$0$以外の場合、鞍点の様子がどのように変わるか、観察してみなさい。
3. $h(s) = s - \frac{1}{s}$の場合、ふたつの鞍点 $s_0= \pm i$ が存在する。そのときの実部$u(s)$の様子を観察してみなさい。

　ヒント：

（この先はこれから）