Pythonプログラミング（その他のトピック・複素写像とスミスチャート）

複素数の写像

複素数$z$を別の複素数$w$に写像する操作 $$ w = f(z) $$ を考えてみよう。実変数の場合は関係をグラフで表現できるので直感的なイメージを得やすいが、 複素数では実部と虚部を対にして考えなければならないので、慣れるには時間がかかるかもしれない。

そこで、ここではNumPyとMatplotlibを使って、複素関数の様子を可視化してみたい。

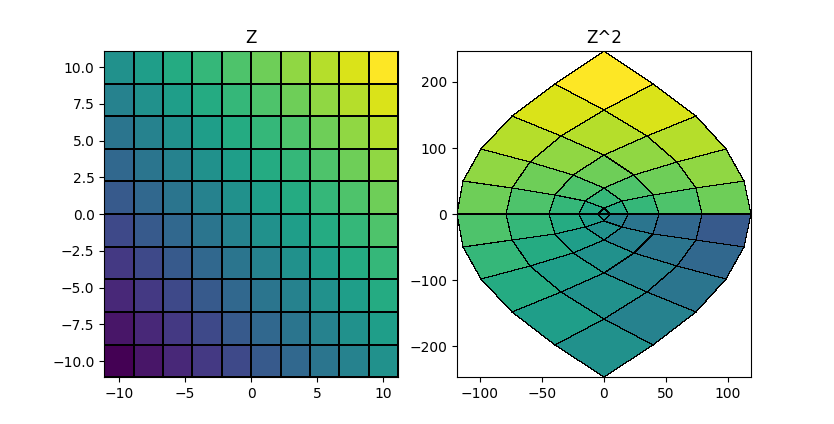
そのために、まず$z$の複素平面を格子状に区切って、格子が$w$のどこに写されるのかを表示することにする。 例えば、$z$の実部を$(-10,10)$の範囲で等間隔に10点、虚軸に沿っても$(-10,10)$の範囲で等間隔に10点に分割し、 それぞれの格子点での実部を配列 ZR、虚部を配列 ZI に設定し、 各格子点での複素値を二次元配列 Z に格納する操作は、 NumPyを使うと、以下のように書くことができる。

import numpy as np

N=10

R = np.linspace(-10,10,N)
X = np.linspace(-10,10,N)
ZR,ZI = np.meshgrid(R,X)

Z = ZR + ZI*1j

ここで、numpy.meshgrid(1次元配列,1次元配列)は、横と縦のそれぞれの格子点の座標を与えると、 それを元に格子（メッシュ）点x座標とy座標のそれぞれを二次元配列として出力する関数である。

複素写像として $f(z) = z^2$を考えてみると、格子点毎の写像先の値の配列は

W = Z*Z

と書くだけで事足りる。

次いで、Wの実部と虚部を取り出して、$w$平面の座標としてプロットする：

WR = np.real(W)
WI = np.imag(W)

import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.pcolormesh(ZR, ZI, ZI+ZR, edgecolors='black', lw=0.005, shading='auto')
ax1.set_title("Z")
ax2.pcolormesh(WR, WI, ZI+ZR, edgecolors='black', lw=0.01, shading='auto')
ax2.set_title("Z^2")
plt.show()

このコードを実行すると、左に$z$平面の格子、右にそれを写像した際の対応する格子がプロットされる。 格子点の色は、$z$平面での格子点の実部と虚部の和に応じてつけられており、同じ色の区画が、写像の前後で対応している。

図で縦横の縮尺が違っているのでわかりにくいが、正則な複素写像は等角写像であることから、$z$平面で直交する格子は、$w$の各点でも直交することも確認できる。

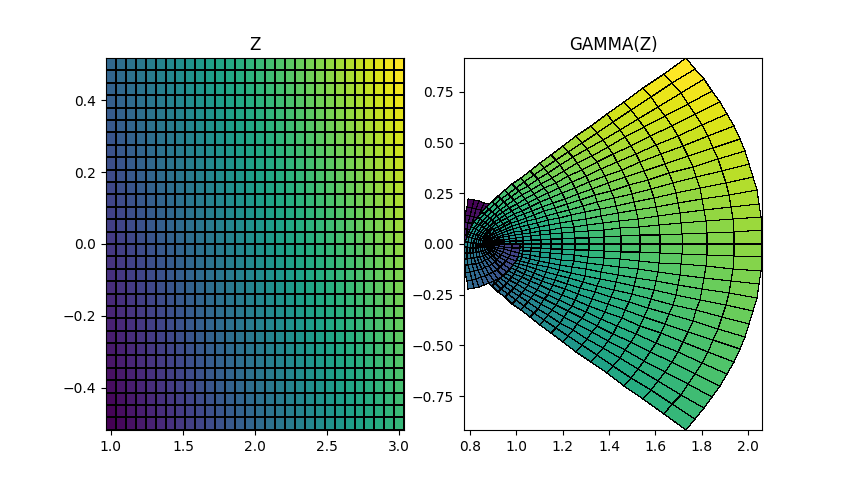
違った例として、ガンマ関数について写像前後の対応関係を格子状にプロットするコードの例を示す：

# coding: utf-8
import numpy as np
from scipy.special import gamma
import matplotlib.pyplot as plt

N=30

R = np.linspace(1,3,N)
X = np.linspace(-0.5,0.5,N)
ZR,ZI = np.meshgrid(R,X)

Z = ZR + ZI*1j

W = gamma(Z)

WR = np.real(W)
WI = np.imag(W)

fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.pcolormesh(ZR, ZI, ZI+ZR, edgecolors='black', lw=0.005, shading='auto')
ax1.set_title("Z")
ax2.pcolormesh(WR, WI, ZI+ZR, edgecolors='black', lw=0.01, shading='auto')
ax2.set_title("GAMMA(Z)")
plt.show()

ガンマ関数は $z=0,-1,-2,-3,\cdots$ に極を持つ（それらの点で発散する）ため、この例では、$\Re(z) \ge 1$の範囲に制限した。

　練習：複素関数

他の複素写像の例について、同様のプロットを作成してみなさい。

スミスチャート

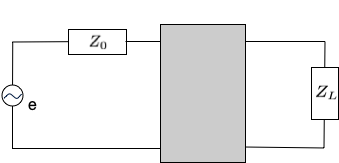
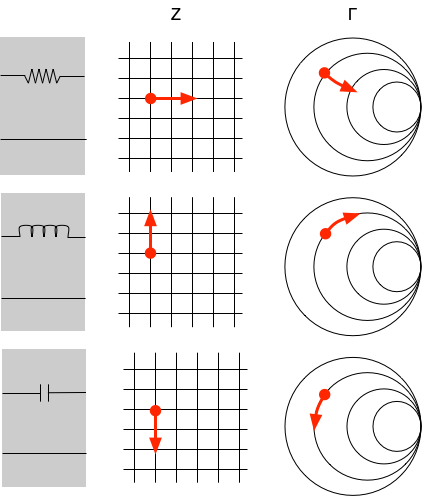
電子回路を学んでいると、信号源のインピーダンス$Z_0$と、負荷のインピーダンス$Z_L$をマッチングさせなければならいケースがしばしば生じる。 そのために、下図のように、グレーの箱の中にどのような（集中定数または分布定数）回路を入れればよいかを考えることになる。

そのような際に登場するのが以下のようなスミスチャート（Smith chart)で、なんだかとても複雑そうな図になっている：

信号源と負荷のインピーダンスが異なる場合、境界で信号の反射が起こる。その程度は、進行波の振幅と反射波の振幅の比$\Gamma$で表すことができて、 信号源側に反射する方向を正にとると、 $$ \Gamma = \frac{Z_L - Z_0}{Z_L + Z_0} $$ と表すことができる。$Z_0$を基準に考えるといろいろと都合が良いので、これを $$ \Gamma = \frac{Z_L/Z_0 - 1}{Z_L/Z_0 + 1} $$ と書き直して、$Z = Z_L/Z_0$ を定義すると、$Z_0$を単位にした反射係数は $$ \Gamma = \frac{Z - 1}{Z + 1} $$ となる。 言うまでもなく、この反射係数が0となるような状態がマッチングが取れた状態、ということになる。

上記の表式は、複素数$Z$から複素数$\Gamma$への写像に他ならない。 そして、$\Gamma$空間の中に、$Z$の値（抵抗値とリアクタンス値）を書き込んで、対応関係を図示したのがスミスチャートに他ならない。

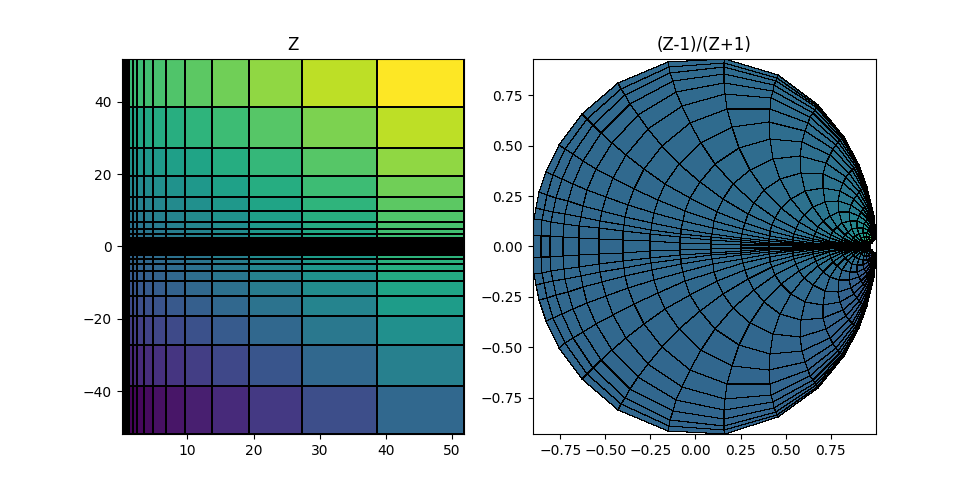
そこで、前節の複素写像の可視化のコードを少し書き換えて、（不格好な）スミスチャートを表示するようにしたコードが以下である。 インピーダンス$Z$の実部（抵抗成分）は非負であるから、それに応じて定義域が異なる点と、$Z$平面での格子の間隔は等比級数的に 変わるようにしている点が、主な変更点である。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt

N=20

R = np.array([2**((i-8)/2) for i in range(N)])

W = np.array([2**((i-8)/2) for i in range(N)])

X = np.hstack([np.flip(W), np.zeros(1), -W])

ZR,ZI = np.meshgrid(R,X)

Z = ZR + ZI*1j

S = np.divide(Z-1,Z+1)

SR = np.real(S)
SI = np.imag(S)

fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.pcolormesh(ZR, ZI, ZI+ZR, edgecolors='black', lw=0.005, shading='auto')
ax1.set_title("Z")
ax2.pcolormesh(SR, SI, ZI+ZR, edgecolors='black', lw=0.01, shading='auto')
ax2.set_title("(Z-1)/(Z+1)")
plt.show()

写像によって、$Z$の虚軸に並行な直線は$\Gamma$平面では実軸上に中心を持つ円に写される。 また、$Z$の実軸に並行な直線も、$\Gamma$では（中心と半径がリアクタンスに依存した）円の一部に写される。

こうした対応関係を念頭に入れると、負荷に直列に素子を追加した際の反射の様子を、図上で表すことが可能となる：

　練習：アドミッタンスチャート

負荷に並列に素子を追加した場合の反射の様子を表すアドミッタンスチャートを、同様にプロットしてみなさい。

　ヒント

　解説: メビウス変換

反射係数をインピーダンス$z$の関数 $$ f(z) = \frac{z-1}{z+1} $$ と思うと、これはメビウス変換(Möbius transformation)と呼ばれる写像 $$ f(z) = \frac{a z + b}{c z + d} $$ (ただし、$ad - bc \neq 0$)の一種に他ならない。 メビウス変換は、複素平面上の円を円に写すことが一般に示すことができる。 ここで、直線も（半径無限大の）円に含めて考える。

ここでは、レジスタンス（$Z$の実部）が一定で、リアクタンス（$Z$の複素部）が変化したときのスミスチャート上の軌跡を考えてみる。 $$ w = \frac{z-1}{z+1} $$ と置くと、逆写像は $$ z = \frac{1+w}{1-w} $$ となる。 ここで、 $$ z = r + x i $$ とおいて、レジスタンス $r$ は一定で、$x$ のみが変化するとする（$r,x$はいずれも実数。また、$r \ge 0$）。

すると $$ r + x i = \frac{1+w}{1-w} $$ となるが、$w \neq 1$の場合 $$ (r + x i) (1-w) = 1+w $$ これを整理して $$ i x (1 - w) = (1-r) + (1+r) w $$ この両辺に $1-\bar{w}$を乗じて（ただし $\bar{w}$は$w$の複素共役） $$ i x (1 - w)(1-\bar{w}) = \left\{ (1-r) + (1+r) w \right\} (1 - \bar{w}) $$

上式の右辺を整理すると $$ i \left(x - (w+\bar{w}) + w \bar{w} \right)= -(w - \bar{w}) + (1-r) + r (w+\bar{w}) - (1+r) w \bar{w} $$ となるが、$w+\bar{w}$は実数、$w-\bar{w}$は純虚数であることに注意して、上式の実部のみを取り出すと $$ (1+r) w \bar{w} - r (w+\bar{w}) - (1-r) = 0 $$ を得る。この式を「平方完成」すると $$ \left( w - \frac{r}{r+1} \right) \left( \bar{w} - \frac{r}{r+1} \right) - \frac{1}{(r+1)^2} = 0 $$ すなわち $$ \left| w - \frac{r}{r+1} \right| = \frac{1}{r+1} $$ であるので、スミスチャート上で中心が$r/(r+1)$、半径が$1/(r+1)$の円を描くことがわかった。

（書きかけ）