「Pythonプログラミング」（その他のトピック・KdV方程式とソリトン）

Pythonプログラミング（その他のトピック・KdV方程式とソリトン）

このページでは、代表的なソリトンの例であるKdV方程式のシミュレーションを試みてみよう。併せて、時間変化する現象の可視化方法についても、何通りか試してみることにする。（ここはこれから）

津波を記述する方程式

底面が平らなプールに水が満たされているとき、その表面に立つ波を考えてみる。波の波長がプールの深さよりも十分に長く、その振幅はプールの深さより十分に小さい状況で、非圧縮（水の密度がどこでも一定）で渦はなく、粘性も無視できるなどの仮定を置くと、いわゆる浅水波を記述する方程式が得られる。プールの縦の断面を取って、横方向をx軸として、水面の平均的な高さを$h$とし、平均水面からの高さの変動を$\eta$で表すことにする。そのような場合、表面が上下に揺れると位相速度$c_0 = \sqrt{gh}$の「重力波」（$g$は重力加速度）が生じること知られている。海洋を伝搬する津波は、水深に比べて十分に長い波長を持つことが知られ、まだその振幅は水深よりも十分に小さいため、「浅い波」とみなすことができる。海洋を津波が高速で伝搬するのは、水深$h$が大きいためである。

表面に立つ波の性質をさらに詳しく調べ、流体力学的な非線形効果まで考慮すると、波の振る舞い方が異なってくることが Korteweg-de Vriesらによって明らかになった（再発見された）。座標を線形波の速さで動いている座標系に取り直すと（$x \leftarrow x - c_0 t$）、波動を表す式は $$ \frac{\partial \eta(x,t)}{\partial t} + \frac{3 c_0}{2h} \eta(x,t) \frac{\partial \eta(x,t)}{\partial x} + \frac{c_0 h^2}{6} \frac{\partial^3 \eta(x,t)}{\partial x^3} = 0 $$ となり、これは（再）発見者の名前にちなんでKorteweg-de Vries (KdV)方程式と呼ばれている。

変数のスケールを取り直すことによって、各項の係数を調整することができる。標準的な形として $$ \frac{\partial u(x,t)}{\partial t} + 6 u(x,t) \frac{\partial u(x,t)}{\partial x} + \frac{\partial^3 u(x,t)}{\partial x^3} = 0 $$ がよく登場するので、以下ではこれを考えることにする。

（書きかけ）

KdV方程式とソリトン

KdV方程式には様々な（無限の）解が存在することが知られている。ひと山のパルスが伝搬する解は1-ソリトン解と呼ばれ、位相速度を$c = 4 \kappa^2$と置くと、 $$ u(x,t) = 2 \kappa^2 \textrm{sech}^2\left(\kappa(x-c t + \delta) \right) $$ と表現される。$c$は正であるから、波動はxが正の方向にのみ伝搬することがわかる。また、山の高さ（振幅）が大きい波ほど、伝搬速度が大きくなるのは、線形波動と大きくことなる点である。

解の導出は専門書に譲って、これが本当に方程式の解になっているかどうか、式に代入して確認してみることにしよう。以下はsympyを使って、上記の解をKdV方程式に代入し、方程式が成り立つかどうか（結果が0になるかどうか）を調べるコードの例である：

from sympy import *

x,t,u,kdveq = symbols("x, t, u, kdveq")
k,c,d = symbols("k, c, d")

c = 4*k**2
u = 2 * k**2 * sech(k*(x-c*t+d))**2

kdveq = diff(u,t) + 6 * u * diff(u,x) + diff(u,x,3)

print(simplify(kdveq))

sympyには代表的な関数はすでに定義されており、双曲線関数 $\textrm{sech}(x) = \frac{2}{e^x + e^{-x}}$ もそのまま記述することができる。

（書きかけ）

離散フーリエ変換による微分の計算

以下では、Numerical Solution of the KdVに述べられている方法を参考に、 KdV方程式を数値的に解くための具体的なコードを考えてみよう。

KdV方程式のシミュレーションには、一階および三階の空間微分を精度よく行う必要がある。そのためには、スペクトル精度を持つFFTを使った微分計算が有効である。具体的、関数 $u(x)$の空間微分は以下の手順で求めることができる。

長さ$L$の区間を$\Delta x = L/N$の幅に等分して（$N$は分割数）、$\ell$番目の区画の座標を $x(\ell) = \Delta x \, \ell$ と置く。説明の便宜上$\ell=0$を原点に対応させるが、座標がシフトしても以下の議論は全く同様である。 $x$の関数$u(x)$を考え、その離散フーリエ変換を $$ U_k = \sum_{\ell=0}^{N-1} u_\ell \exp\left( -\frac{2 \pi k x(\ell)}{L} i\right) $$ と定義することにする。ここで、座標が離散的に指定されていることを明示するため、同じことであるが、 $$ U_k = \sum_{\ell=0}^{N-1} u_\ell \exp\left( -\frac{2 \pi k \ell}{N} i\right) $$ と書いておく。その逆変換は、 $$ u_{\ell} = \frac{1}{N} \sum_{k=0}^{N-1} U_k \exp\left( \frac{2 \pi k x(\ell)}{L} i\right) $$ となる。

これを使うと、一階微分は $$ \begin{eqnarray} \frac{\partial u(x)}{\partial x} & = & \frac{1}{N} \sum_{k} \left(\frac{2 \pi i k}{L} \right) U_k \exp\left( \frac{2 \pi k x(\ell)}{L} i\right) \\ & = & \frac{1}{N} \sum_{k} \left(\frac{2 \pi i k}{\Delta x \, N} \right) U_k \exp\left( \frac{2 \pi i k \ell}{N} i\right) \end{eqnarray} $$ のように、元のフーリエ成分に $\frac{2 \pi i k}{\Delta x \, N}$という因子を乗じると、微分のフーリエ成分が得られることがわかる。ただし、フーリエ空間の折返し構造から、乗ずる因子を、 $k \le N/2$では $$ \frac{2 \pi i k}{\Delta x \, N} $$ $k \gt N/2$ については $$ \frac{2 \pi i (k-N)}{\Delta x \, N} $$ とする必要がある。そのあたりの事情については、チューリングパターンのページで説明したので参照のこと。

全く同様に、$k \le N/2$については $\left( \frac{2 \pi i k}{\Delta x \, N} \right)^3$、 $k \gt N/2$ では $\left(\frac{2 \pi i (k-N)}{\Delta x \, N}\right)^3$を乗じれば、3階微分のフーリエ成分が得られる。

微分方程式の時間発展の記述

解きたいKdV方程式は $$ \frac{\partial u}{\partial t} + 3 \frac{\partial (u^2)}{\partial x} + \frac{\partial^3 u}{\partial x^3} = 0 $$ と書き直すことができる。この式全体を$x$についてフーリエ変換すると $$ \frac{\partial U(q,t)}{\partial t} + 3 i q U_2(q,t) - i q^3 U(q,t) = 0 $$ となる。ただし、ここでは $$ q(k) = \begin{cases} \frac{2 \pi k}{L}, & \text{if } k \leq N/2\\ \frac{2 \pi (k-N)}{L}, & \text{otherwise} \end{cases} $$ と置いて、（離散）フーリエ変換を $$ U(q,t) = \sum_\ell u(x(\ell),t) \exp\left( - i q(k) x(\ell) \right) $$ $$ U_2(q,t) = \sum_\ell \left\{ u(x(\ell),t) \right\}^2 \exp\left( - i q(k) x(\ell) \right) $$ で定義した。

フーリエ変換したKdV方程式は$t$についての常微分方程式と見なせるから、これをオイラー差分で近似すると、$u(x,t)$のフーリエモードの時間発展を表す差分方程式 $$ U(q,t+\Delta t) = U(q,t) + \left[ - 3 i q U_2(q,t) + i q^3 U(q,t) \right] \Delta t $$ が得られる。 $U(q,t)$と$U_2(q,t)$が含まれているように見えるが、 $U_2(q,t)$は、時間ステップ毎に$U(q,t)$を逆フーリエ変換して$u(x,t)$を得てから、それを二乗した関数をフーリエ変換することで得られるので、閉じた関係式を形成できる（その過程で、異なる波数の波の相互作用が生じる）。

ただし、このスキームをそのまま適用すると、誤差が累積して短時間で計算が破綻してしまう。そこで、こちらのサイトでは、 $$ U(q,t+\Delta t) = U(q,t) + 3 i q^3 U(q,t) \Delta t $$ の部分が線形で厳密に解けることから $$ U_1(q,t+\Delta t) = U(q,t) \exp\left(i q^3 \Delta t\right) $$ という途中段階を経てから $$ U(q,t+\Delta t) = U_1(q,t+\Delta t) - 3 i q U_2(q,t+\Delta t) \Delta t $$ を得る方法を提案している。ここで、$U_2(q,t+\Delta t)$は、$U_1(q,t+\Delta t)$を逆フーリエ変換して得た$u_1(x,t+\Delta t)$を自乗してフーリエ変換した $$ \begin{eqnarray} u_1(x,t+\Delta t) & \leftarrow & \mathcal{F}^{-1}[U_1(q,t+\Delta t)] \\ U_2(q,t+\Delta t) & \leftarrow & \mathcal{F}\left[ \left\{ u_1(x,t+\Delta t) \right\}^2 \right] \end{eqnarray} $$ を用いると良いとされている（$\mathcal{F}[\cdot]$はフーリエ変換、$\mathcal{F}^{-1}[\cdot]$はその逆変換）。

Pythonによるコーディングの例

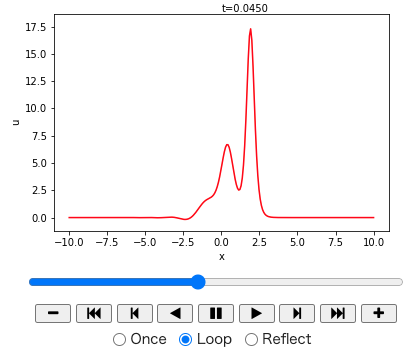
以下は $L=20$の区間（周期境界）で、初期条件 $$ u(x,0) = 12 \exp\left(- x^2 \right) $$ のもとで計算し、アニメーション表示するコードの例である。

時間方向の積分は関数nextstep()の中に書かれており、前節のアルゴリズムそのままではなく、中点法を使って $$ \begin{eqnarray} U_1(q,t+\Delta t) & \leftarrow & U(q,t) \exp\left(i q^3 \Delta t\right) \\ K_1 & \leftarrow & - 3 i q \mathcal{F}[u^2] \\ U_2(q,t+\Delta t/2) & \leftarrow & U_1(q,t+\Delta t) + K_1 \Delta t/2 \\ u_2(x,t+\Delta t/2) & \leftarrow & \mathcal{F}^{-1}[U_2(q,t+\Delta t/2)] \\ K_2 & \leftarrow & - 3 i q * \mathcal{F}[u_2(x,t+\Delta t/2)^2] \\ U(q,t+\Delta t) & \leftarrow & U_1(q,t+\Delta t) + K_2 \Delta t \\ \end{eqnarray} $$ によって行っている。

このコードはGoogle Colaboratoryで実行することを想定。

単体で実行する場合は、末尾付近のplt.close()の行はplt.show()に変更すること。

import numpy as np
import random
import math
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

def prep_3iq(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 3*1j*q
    return A

def prep_iq3(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 1j*q*q*q
    return A

def nextstep():
    global u,t
    U = np.fft.fft(u)    
    for cnt in range(500):
        U1 = U * np.exp(OP_iq3 * dt)
        K1 = - OP_3iq * np.fft.fft(u*u)
        U2 = U1 + K1 * dt/2
        u2 = np.fft.ifft(U2).real
        K2 = - OP_3iq * np.fft.fft(u2*u2)
        U = U1 + K2 * dt
        u = np.fft.ifft(U).real
        t = t + dt

###
N = 256
L = 20
dx = L/N

OP_3iq = prep_3iq(N,dx)
OP_iq3 = prep_iq3(N,dx)

x = np.linspace(-L/2,L/2,N)
u = np.exp(-x*x)*12

HSCALE=4
VSCALE=10
H = 800

fig, ax = plt.subplots()
images = []

t = 0
dt = 0.00001

ax.set_xlabel('x')
ax.set_ylabel('u')

while t<0.1:
    img = ax.plot(x,u,color='red')
    label = plt.text(0.5,1, 't='+'{:.4f}'.format(t), ha='left',va='bottom',color='black', transform=ax.transAxes)
    images.append([img[0],label])
    nextstep()

anim = animation.ArtistAnimation(fig, images, interval=100)
rc('animation', html='jshtml')
plt.close()
anim

上のコードをGoogle Colaboratoryのノートブック上で実行している様子。

上のコード例は、計算結果をプロットした画像をあらかじめ蓄えておいて、紙芝居のように表示するようにしているので、長時間にわたる表示には向いていない。

そこで、pygletを使って、画面に直接描画出力するコードの例も以下に示しておく。

このコードを実行するには pyglet(バージョン1.5.27以前) が必要

pyglet version 2をお使いの方は kdv-eq-pyglet2.pyをダウンロードしてお使いください。

# coding: utf-8

import numpy as np
import random
import math
import pyglet
from pyglet.gl import *

def prep_3iq(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 3*1j*q
    return A

def prep_iq3(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 1j*q*q*q
    return A

###
N = 256
L = 20
dx = L/N

OP_3iq = prep_3iq(N,dx)
OP_iq3 = prep_iq3(N,dx)

x = np.linspace(-L/2,L/2,N)
u = np.exp(-x*x)*12

t = 0
dt = 0.00001

HSCALE=4
VSCALE=10
H = 800
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*HSCALE,H,config=config,resizable=False)
win.set_caption('KdV Equation')

def nextstep():
    global u,t
    U = np.fft.fft(u)    
    for cnt in range(500):
        U1 = U * np.exp(OP_iq3 * dt)
        K1 = - OP_3iq * np.fft.fft(u*u)
        U2 = U1 + K1 * dt/2
        u2 = np.fft.ifft(U2).real
        K2 = - OP_3iq * np.fft.fft(u2*u2)
        U = U1 + K2 * dt
        u = np.fft.ifft(U).real
        t = t + dt
    

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0,1)
    glColor3d(0.2,0.2,0.3)
    glLineWidth(2.0)    
    for j in range(-100,100,10):
        glBegin(GL_LINES)
        glVertex2d(0, H/2 + VSCALE*j)
        glVertex2d(N*HSCALE, H/2 + VSCALE*j)
        glEnd()
        str = '{0}'.format(j)
        label_y = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=20, y=H/2+VSCALE*j-6)
        label_y.draw()
    
    glColor3d(1.0, 0.5, 0.1)
    glLineWidth(4.0)
    glBegin(GL_LINE_STRIP)    
    for i in range(N):
        glVertex2d(i*HSCALE, H/2+u[i]*VSCALE)
    glEnd()

    str = '{0}'.format(-L/2)
    label_x0 = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=0, y=H/2-25)
    label_x0.draw()

    str = '{0}'.format(L/2)
    label_x1 = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=N*HSCALE-40, y=H/2-25)
    label_x1.draw()

    str = 'T={0:.3f}'.format(t)
    label_time = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=10, y=10)
    label_time.draw()

def update(deltat):
    nextstep()    


pyglet.clock.schedule_interval(update, 1/20.0)
pyglet.app.run()

上のコードを実行した様子が以下の動画である（YouTube）。初期条件として単峰の山（ガウス曲線）を与えると、それが複数の孤立波（ソリトン）に分裂し、進行する様子が観察できる。振幅の大きな波ほど伝搬速度（位相速度）が大きいことも判る。

　練習：積分スキームの比較

上のコードの関数 nextstep()中の積分のスキームを

オイラー差分（１次）
4次のルンゲクッタ

に変更し、それぞれの動作や安定性を確認してみなさい。

　解説: Waterfall型のプロット

下図のように、波動の伝搬の様子を時空間的に可視化し、アニメーション表示するコードの例を示す。時間が「上」から「下」に流れるように表示されるので waterfall plotと呼ぶことがある。ソリトンが衝突し、再び分裂して進行する様子がよく確認できる（YouTube動画)。

計算部分は上記の例と全く同様であるが、計算結果を配列に格納・操作し、それを画像として表示することで、画面の更新をいくばくか高速化している。

NumPyの配列を画像として扱う際に、画像の横軸が「列」（axis=1）、画像の縦軸が「行」（axis=0)に対応する点に注意が必要である。

このコードを実行するには pyglet(version 1.5以下)が必要

pyglet version 2をお使いの方は kdv-eq-scroll-pyglet2.pyをダウンロードしてお使いください。

#coding utf-8

import numpy as np
import random
import math
import pyglet
from pyglet.gl import *

def prep_3iq(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 3*1j*q
    return A

def prep_iq3(n,dx):
    A = np.zeros((n,),dtype=np.complex64)
    for k in range(0,n):
        q = 2*math.pi*k/(dx*n) if k<=n//2 else 2*math.pi*(k-n)/(dx*n)
        A[k] = 1j*q*q*q
    return A

###
N = 256
L = 20
dx = L/N

OP_3iq = prep_3iq(N,dx)
OP_iq3 = prep_iq3(N,dx)

x = np.linspace(-L/2,L/2,N)
u = np.exp(-x*x)*12

t = 0
dt = 0.00001

SCALE=1
H = 400

IMG_DATA = np.zeros(shape=(H,N*SCALE,3),dtype=np.uint8)

config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,H,config=config,resizable=False)
win.set_caption('KdV Equation')
def nextstep():
    global u,t,umem
    U = np.fft.fft(u)
    for cnt in range(100):
        U1 = U * np.exp(OP_iq3 * dt)
        K1 = - OP_3iq * np.fft.fft(u*u)
        U2 = U1 + K1 * dt/2
        u2 = np.fft.ifft(U2).real
        K2 = - OP_3iq * np.fft.fft(u2*u2)
        U = U1 + K2 * dt
        u = np.fft.ifft(U).real                
        t = t + dt

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0,1)
    global IMG_DATA,u
    IMG_DATA = np.roll(IMG_DATA,1,axis=0)
    for i in range(N):
        r = int((math.sin(u[i]*0.1)+1)/2*255)
        g = int((math.sin(2*u[i]*0.1)+1)/2*255)
        b = int((1.0+math.cos(u[i]*0.1))/2*255)
        IMG_DATA[0,i*SCALE:(i+1)*SCALE,0] = r
        IMG_DATA[0,i*SCALE:(i+1)*SCALE,1] = g
        IMG_DATA[0,i*SCALE:(i+1)*SCALE,2] = b
    pixels = IMG_DATA.ravel()
    rawData =  (GLubyte * len(pixels))(*pixels)
    imageData = pyglet.image.ImageData(N*SCALE, H, 'RGB', rawData)
    imageData.blit(0, 0)

    glColor3d(1,1,1)
    glLineWidth(1)
    glBegin(GL_LINE_STRIP)
    glVertex2d(1, H-10)
    glVertex2d(1, H-20)
    glVertex2d(N*SCALE, H-20)
    glVertex2d(N*SCALE, H-10)        
    glEnd()
        
    str = '{0}'.format(-L/2)
    label_x0 = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=10, x=0, y=H-30)
    label_x0.draw()

    str = '{0}'.format(L/2)
    label_x1 = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=10, x=N*SCALE-30, y=H-30)
    label_x1.draw()

    str = 'T={0:.3f}'.format(t)
    label_time = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=10, x=N*SCALE/2-30, y=H-12)
    label_time.draw()

def update(deltat):
    nextstep()    

pyglet.clock.schedule_interval(update, 1/20.0)
pyglet.app.run()

（これから）