拡散律速凝集モデル
このページでは、ランダムなフラクタルパターンを生成する拡散律速凝集モデルについて紹介する。
1.ランダムウォークする粒子の非可逆な凝集
何等かの種から出発してモノが成長する現象を考えてみよう。 例えば、ひとつの卵細胞が分裂しながら生物の体が形成されたり、ひとつのカビの胞子から菌糸が伸びて折角の食品を台無しにしたり、 空中の小さなチリ等が核となって雪の結晶となったり、目に見えないくらいの小さな亀裂が広がって構造物全体に広がったり、等々、 考え始めるといくらでも例を挙げることができるだろう。
こうした現象は一般にとても複雑で、取り付く島も無さそうだけれども、一旦そのことは忘れることにして、 以下のような単純化された成長のルール(アルゴリズム)を考えてみよう。
2次元拡散律速凝集
Input: クラスターの粒子数
Output: 凝集した粒子の集合
1: 2次元平面の上に種粒子を1つ置き、初期クラスター(凝集体)とする
2: 8:までを反復する:
3: クラスターから離れた点からランダムウォーカーを放ちランダムウォークさせる:
4: もしランダムウォーカーがクラスターに接したら:
5: そこで動きを止め、クラスターの一部に加える
6: 決められた粒子数に達したら 9:に、そうでなければ 3:から反復する
7: もしランダムウォーカーが遠方に去ってしまったら 3:からやり直す
8: 外側の反復ここまで
9: クラスターを構成する粒子の位置を出力して終了する
このアルゴリズムの様子を掴んでもらうため、ホワイトボード上に種粒子として青色のマグネットを置き、 その周囲からランダムウォーカー(赤色のマグネット)を放って、クラスターに凝集させる様子を ストップモーション動画にしてみたのが以下である。
このアルゴリズムは、理想的には無限遠方から到来するランダムウォーカー(拡散粒子)が非可逆的に凝集を繰り返す過程を模したものである。 ただし、凝集は種を中心としたクラスターの周囲のみで生じ、ランダムウォーカー同士の結合などは考えない(漂っている粒子は常に1個だけ)。 このモデルは、WittenとSanderによって1981年に提案され、拡散律速凝集(diffusion-limited aggregation; DLA)モデルと呼ばれ、 以来、多数の研究が行われてきた。
ランダムウォーカーが表面に到来すると「その瞬間」に付着するということは、拡散が全体を律速している一番「遅い」過程であるということになり、 それが「拡散律速」の由来である。 その反対に、粒子の付着(反応)確率が非常に小さいような場合は、到来した粒子は付着(反応)が成功するまであちらこちらを彷徨うことになり、そのような状況は「反応律速」と呼ばれる。
単純なモデルではあるが、凝集する粒子数を増やしていくと複雑な樹枝状のパターンが出現し、 全体と部分が統計的な意味で相似になっている(一部を拡大すると全体と同様の構造が出現する)ような、フラクタル(自己相似)な性質を持つことが分かっている。
更に、単なるコンピューター上の単なる「おもちゃ」にとどまらず、このDLAモデルは自然現象の理解にも繋がっている。
一例として、雷などの放電現象との関係について、 ラプラス方程式 のページで触れているので、参照のこと。
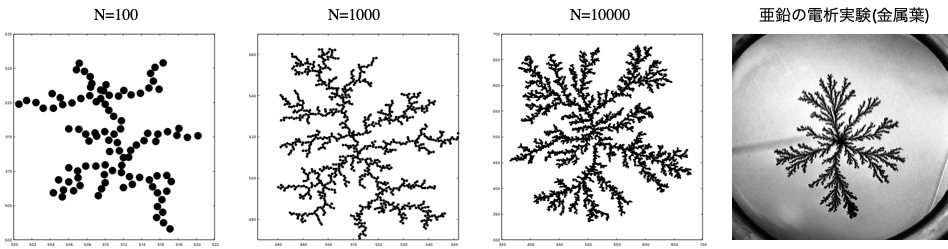
クラスターの数を100,1000,10000と増やしていった際のパターンの様子。 右端は電析実験によって得られた金属結晶(金属葉)の例。
2.DLAのシミュレーション
愚直に一歩ずつ粒子をランダム・ウォークさせながらDLAのシミュレーションを行うことも可能ではあるが、恐ろしく時間がかってしまう。 そこで、以下では、効率よくミュレーションを行うための工夫やポイントをいくつかまとめておく。
2次元ランダムウォーク
ランダム・ウォーカーを動かすには、2次元の格子(正方格子や三角格子)上の近接点に等しい確率で移動させる方法(on-lattice simulation)と、 等しい確率であらゆる方向にジャンプすることを許すやり方(off-lattice simulation)が考えられる。 以下では後者の例について考えることにする。 ここで重要なのは、境界やクラスター(凝集体)が存在しない空間では、ある点$(x_0,y_0)$から出発したランダムウォーカーは その点を中心とした円上にいずれ到達するが、その到達確率は円上の全ての点で等しいことである。 なお、こうしたランダムウォークの等方性は、格子上のランダムウォークであっても同様である。
ランダムウォークの開始位置
無限遠方から出発したランダムウォーカーが、クラスターとは交差しないような、クラスターの外側に設定された円周上の点に初めて到達する確率は、 ランダムウォークの等方性から、その円周上で等しくなる。 したがって、クラスターを包含するような円を描いて、その円周上の点をランダムに選び、そこからランダムウォークを開始すれば十分である。
ランダムウォークの歩幅と方向の設定
境界等の無い領域では、ランダムウォーカーは円周上の点に当確率で到達するため、クラスターのどの点とも交わらないような長さを求めて、 その距離分だけ、ランダムな方向にジャンプさせるのが効率的である。 言い換えれば、DLAでは現象が進行する物理的な時間は全く問題にしない(あるいは、極めて遅い極限を考えている)ので、1ステップずつ拡散過程を追いかける必要は無い。
2次元の場合は、ジャンプする方向角を $(0,2\pi]$ の間の一様乱数で生成しても良いが、より汎用性のある方法としては、 ガウス分布に従う独立な乱数を2つ生成し長さを規格化することで、任意の次元で球面上に一様に分布する乱数が生成できる。
遠方から到達したランダム・ウォーカーは、クラスターより大きな円周上の点に等しい確率で1度目は到達する(左)。 クラスターと交わらない円の半径をステップ長として取ることができる(右)。
付着の判定
格子モデルの場合は、ランダムウォーカーが クラスターとして専有されているサイトの最近接に到来した際に、そこで固定して、クラスターの一部とすればよい。
off-latticeの場合は、クラスターを構成する粒子にウォーカーが一定の距離以下に近づいた際に接触したものと判定し、接触したクラスター側の粒子から、あらかじめ定義しておいた粒子径(例えば1)だけ離れた位置に「微調整」してから固定する。 その細かい手順には任意性が残るが、最終的に出来上がるクラスターの構造(フラクタル性等)には影響しない。
3.コードとシミュレーション
Pythonは実行速度の点でこの種のシミュレーションにあまり向かないものの、著者が過去にFortranで書いたコードをPythonに書き直した例を以下に示す。 クラスターとして専有されている位置を配列を使って「地図化」し、クラスターと重ならない円の大きさを高速で判定できるよう工夫している。 FortranやCほどは速くないものの、このコードでも数万粒子程度までのシミュレーションは可能である。
多数の点をプロットする際にmatplotlibでは効率が悪いので、 datashaderを用いラスター画像を生成してから表示するようにしている。
# Diffusion-Limited Aggregation in 2-d
# originally written in FORTRAN
# 2024, Yoshinori Hayakawa
import numpy as np
import random
import math
LSIZ=513
NCLUSTER=100000
NDIM=2
CGF=2
LAYER=0.2
MF=10
OF=15
NOFFSET=10
class Dla2d:
noa=0
r_tip=0.0
r_kill=0.0
def __init__(self):
self.init_vars()
self.set_seed()
def init_vars(self):
self.u = np.zeros(shape=(LSIZ,LSIZ),dtype=np.uint32)
self.pp = np.zeros(shape=(NCLUSTER,),dtype=np.uint32)
self.x_cluster = np.zeros(shape=(NDIM,NCLUSTER))
self.x_walker = np.zeros(shape=(NDIM,))
self.x_cluster[:,0] = (LSIZ-1)*CGF/2
def set_seed(self):
self.r_tip = 0.0
self.r_kill = OF
self.noa = 0
self.x_walker = self.x_cluster[:,0]
self.grow()
def step_fwd(self):
while True:
rr = 0.0
u0 = np.random.normal(0,1,size=(NDIM,))
rr = np.sqrt(np.sum(u0**2))
u0 = u0 / rr
self.x_walker = (self.r_tip + 5.0) * u0 + self.x_cluster[:,0]
if self.random_walk() > 0:
break ; # random_walk == 0 : fail
def get_dist(self):
index = 0
dd = np.linalg.norm(self.x_walker - self.x_cluster[:,0])
if dd > self.r_tip+5.0:
distance = dd - self.r_tip - LAYER
return (index, distance)
step = 5
while True:
ibd = (1 << step) * CGF
ix = self.x_walker.astype(int) // ibd
if (self.u[ix[0],ix[1]] & (1<<step)) == 0:
distance = (2**step) * CGF - 1.0
return (index, distance)
step = step - 1
if step<0:
break
ix = self.x_walker.astype(int) // CGF
dd = 1.0e+30
for i1 in range(ix[1]-1, ix[1]+2, 1):
for i0 in range(ix[0]-1, ix[0]+2, 1):
ell = self.u[i0,i1] >> NOFFSET
while True:
if ell==0:
break
d = np.sum((self.x_cluster[:,ell] - self.x_walker)**2)
if d < dd:
dd = d
index = ell
ell = self.pp[ell]
dd = math.sqrt(dd) - 1.0 # 1 = diameter of paticle
if dd > CGF:
distance = CGF - 1.0
else:
distance = dd
return (index,distance)
def random_walk(self):
while True:
index,distance = self.get_dist()
if distance > LAYER: # large leap
dx = np.random.normal(0,1,size=(NDIM,))
rr = np.sqrt(np.sum(dx**2))
dx = distance * dx / rr
else: # touching the surface
dx = self.x_walker - self.x_cluster[:,index]
rr = np.sqrt(np.sum(dx**2))
dx = dx / rr * (1.0 - rr) # adjust the location
self.x_walker = self.x_walker + dx
return 1
self.x_walker = self.x_walker + dx
rr = np.linalg.norm(self.x_walker - self.x_cluster[:,0]) # check how far from the origin
if rr > self.r_kill:
return 0
def grow(self):
self.noa += 1
self.x_cluster[:,self.noa] = self.x_walker[:]
dd = np.linalg.norm(self.x_walker - self.x_cluster[:,0])
if dd > self.r_tip:
self.r_tip = dd
self.r_kill = MF * self.r_tip + OF
ix = self.x_walker.astype(int) // CGF
k = (self.u[ix[0],ix[1]]) >> NOFFSET
if k==0:
self.u[ix[0],ix[1]] |= (self.noa * (1<<NOFFSET))
self.pp[self.noa] = 0
else:
ell = self.pp[k]
while True:
if (ell==0):
break
k = ell
ell = self.pp[k]
self.pp[k] = self.noa
self.pp[self.noa] = 0
step=0
while step<8:
ibd = (1<<step) * CGF
ix = self.x_walker.astype(int) // ibd
for i1 in range(ix[1]-1,ix[1]+2,1):
for i0 in range(ix[0]-1,ix[0]+2,1):
if i0>=0 and i0<LSIZ and i1>=0 and i1<LSIZ:
self.u[i0,i1] |= (1<<step)
step += 1
return
def print(self):
print(self.x_cluster[0,self.noa], self.x_cluster[1,self.noa])
###########
dla = Dla2d()
N=20000
while dla.noa <=N:
dla.step_fwd()
dla.grow()
cluster = dla.x_cluster
# plotting
import pandas as pd
import datashader as ds
import datashader.transfer_functions as tf
import matplotlib.pyplot as plt
import matplotlib.cm as cm
SIZE = 513
x = cluster[0,:N] - cluster[0,0]
y = cluster[1,:N] - cluster[1,0]
colors = np.linspace(0, 1, len(x))
df = pd.DataFrame({'x': x, 'y': y, 'colors': colors})
canvas = ds.Canvas(plot_width=SIZE, plot_height=SIZE, x_range=(-SIZE/2,SIZE/2), y_range=(-SIZE/2,SIZE/2))
agg = canvas.points(df,'x','y', ds.mean('colors'))
img = tf.shade(agg, cmap=cm.magma)
plt.imshow(img.to_pil(), origin='lower')
plt.title("Diffusion-Limited Aggregation in 2D")
plt.text(10,SIZE-20,"N=" + str(N))
plt.show()
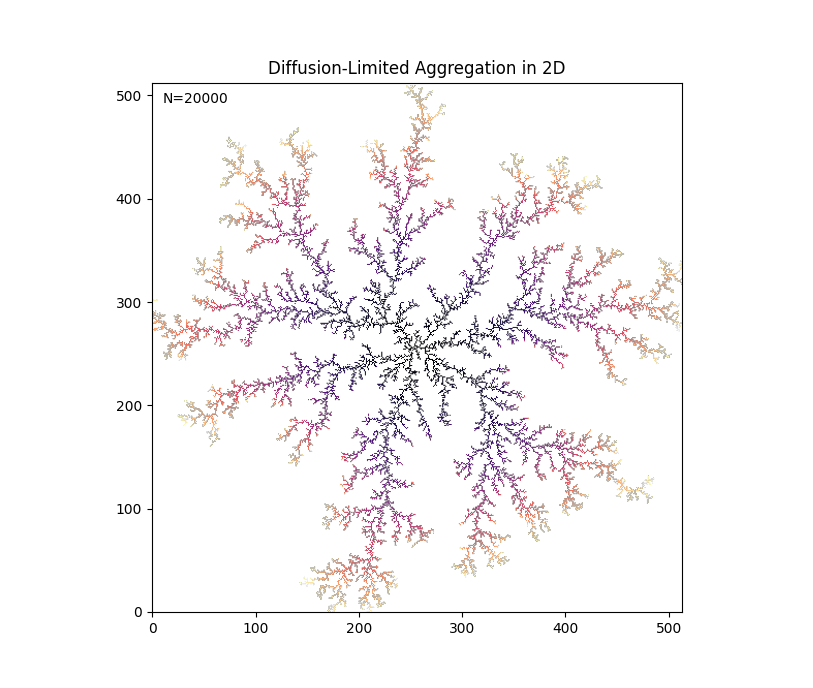
上のコードを走らせて、20000粒子を凝集させた例を以下に示す。
実行には数分程度の時間を要するので、最初はN=20000の箇所をもっと小さな数から試してみるとよい。
成長の様子のアニメーション表示
クラスターに粒子が付着しながら成長する様子をアニメーション表示するコードの例を以下に示す。 実行には pyglet (ver. 2以上) がインストールされたパソコンが必要。 上記のコードのDla2dクラスの定義部分以降を以下で置き換えて実行のこと。
###############
import pyglet
LSIZ=513
CGF=2
WSIZ=LSIZ*CGF
dla = Dla2d()
N=20000
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(WSIZ,WSIZ,config=config,resizable=False)
win.set_caption('Diffusion-limited Aggregation')
circles = [ ]
@win.event
def on_draw():
win.clear()
for c in circles:
c.draw()
n = len(circles)
label = pyglet.text.Label('N='+str(n), font_name='Helvetica', font_size=24, color=(128,128,128,255), \
x=10, y=10, anchor_x='left', anchor_y='bottom')
label.draw()
return
def update(dt):
n = dla.noa
if n < N:
dla.step_fwd()
dla.grow()
cluster = dla.x_cluster
x = (cluster[0,n]-WSIZ/2)*4 + WSIZ/2
y = (cluster[1,n]-WSIZ/2)*4 + WSIZ/2
circle = pyglet.shapes.Circle(x=x, y=y, radius=2, color=(50, 100, 200))
circles.append(circle)
pyglet.clock.schedule(update)
pyglet.app.run()
実行中のウィンドウの様子
 発展練習:3次元DLA
発展練習:3次元DLA
上記のコードを少し手直しすることで、3次元DLAのシミュレーションが可能である。 表示方法も含め、工夫してみなさい。
 ヒント
ヒント
以下にシミュレーションの一例(動画)を示す。構造が確認しやすいように、凝集体をゆっくり回転させている。 3次元DLAはフラクタル的で、そのフラクタル次元は$D \approx 2.5$であることが知られており、中身が「スカスカ」の構造となっている。