Pythonプログラミング（ステップ７・配列・偏微分方程式）

ラプラス方程式とその差分化

物理学などでしばしば登場する代表的な偏微分方程式であるラプラス方程式 $$ \nabla^2 \phi = 0 \tag{1} $$ の数値解法について考えてみよう。 ここでは比較的簡単な二次元の矩形領域について $$ \frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} = 0 \tag{2} $$ を解いてみたい。

まず、$\phi$を$(x,y)$の周りで4通りに展開する： $$ \begin{eqnarray} \phi(x + \delta, y) = \phi(x,y) + \frac{\partial \phi(x,y)}{\partial x} \delta + \frac{1}{2} \frac{\partial^2 \phi(x,y)}{\partial x^2} {\delta}^2 + \cdots \\ \phi(x - \delta, y) = \phi(x,y) - \frac{\partial \phi(x,y)}{\partial x} \delta + \frac{1}{2} \frac{\partial^2 \phi(x,y)}{\partial x^2} {\delta}^2 + \cdots \\ \phi(x, y + \delta) = \phi(x,y) + \frac{\partial \phi(x,y)}{\partial y} \delta + \frac{1}{2} \frac{\partial^2 \phi(x,y)}{\partial y^2} {\delta}^2 + \cdots \\ \phi(x, y - \delta) = \phi(x,y) - \frac{\partial \phi(x,y)}{\partial y} \delta + \frac{1}{2} \frac{\partial^2 \phi(x,y)}{\partial y^2} {\delta}^2 + \cdots \\ \end{eqnarray} $$ そして、上の４式を加えると、一階微分の項はキャンセルされるので $$ \phi(x + \delta, y) + \phi(x - \delta, y) + \phi(x, y + \delta) + \phi(x, y - \delta) = 4 \phi(x,y) + \left[\frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} \right] \delta^2 + \cdots \tag{3} $$ すなわち、ラプラシアンは $$ \frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} \approx \frac{1}{\delta^2} \left[ \phi(x + \delta, y) + \phi(x - \delta, y) + \phi(x, y + \delta) + \phi(x, y - \delta) - 4 \phi(x,y) \right] \tag{4} $$ のようにして差分で近似できることがわかる。

矩形状の空間を碁盤の目状に区切って、左から $i$番目、上から $j$ 番目のマス目の位置を $(i,j)$ で表し、 $\delta=1$とおくと、(2)式のラプラス方程式は、 $$ \phi(i+1, j) + \phi(i-1, j) + \phi(i, j+1) + \phi(i, j-1) - 4 \phi(i, j) = 0 \tag{5} $$ というパターンの差分方程式に帰着される。 この式の形をみると、どの点でも中央の値が周囲の平均値に（「中央」が4つの近傍点の値の和の1/4に等しく）なるように調整されているような状況が、(2)式の解であることがわかる。ラプラス演算子は「エッジ」を検出する作用があるので、ラプラス方程式(1)は、エッジが無くなるような$\phi$の分布を求める式になっている。式(5)は、エッジを無くするための「移動平均」操作と解釈することもできる。

加えて、領域の端点で、$\phi_{i,j}$の値を決めれば（ディリクレ境界条件）、$\{\phi_{i,j}\}$についての連立一次方程式の解として、偏微分方程式の数値解を得ることができる。

空間を　$100\times 100$ に区切った場合でも、変数（未知数）の数は $10000$ 個となるように、解くべき連立方程式は一般に非常に大規模になる。

避雷針の効果のシミュレーション

ラプラス方式で記述できる現象は多数知られているが、静電ポテンシャルはその代表例といえる。 雷雲が発達すると、雲の内部の粒子同士の「摩擦」によって電荷が生じ、上空の電位（電圧）が著しく高まる。 一方地上の電圧は一定なので、上下に大きな電圧の差が生じ、それがある限界を超えると、空気中を短時間に大きな電流が流れる。 こうした雷の発生原理は誰でも知っているが、そのとき、ビルの屋上に立てられた避雷針は、どのような役割を果たしているのだろうか。

矩形領域を$W \times H$の碁盤の目に区切り、 碁盤の目の左からの位置を$x$、上からの位置を $y$、としたとき、 $$ n = x + y \times W $$ というルールで、$n$番目の未知の変数 $\phi_n$ との対応付けを行うことにする： $$ \phi(x,y) = \phi_{x + y W} $$

そして、 矩形の上端（上空）では $ \phi_n = 100 $ 下端（地上）では $ \phi_n = 0 $ とし、さらに、領域の中央に幅1の棒を立て、その棒上でも地上と同じ電位 $\phi_n=0$という境界条件を課す。

左右の辺については、左端が右端と、右端は左端と繋がっていると考える（あるいは、左と右の辺を同一視する）ことで、 横方向にはどこまでも（ただし周期的に）広がる空間を表現することにしよう。

そのとき、(5)式に対応する、解くべき差分方程式は $$ \phi_{x+1+y W} + \phi_{x-1+y W} + \phi_{x+(y+1) W} + \phi_{x+(y-1)W} - 4 \phi_{x+y W} = 0 $$ となる。

上記の式は、連立方程式の1行分に対応するが、連立方程式を行列表現した場合、各行でゼロでない要素は、たかだか5つしか無いことになる。 すなわち、扱うべき行列は 、ほとんどの要素が０であるような疎行列（sparse matrix）となる。 ラプラス方程式に限らず、自然現象においては、各変数が近接の少数の変数としか関係しない場合が多いので、それを扱う際には疎行列よく現れる。 疎行列の計算を行う際は、多くを占める０を記憶しておくのは記憶領域の無駄になるため、各種の工夫を凝らすのが通例である。

以上を踏まえ、実際にPythonでコーディングした例を以下に示す。連立方程式を解くためSciPyの疎行列用のライブラリを用いた。

# coding: utf-8

import numpy as np
from scipy.sparse import lil_matrix,csc_matrix
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt

W = 256
H = 256
N = W*H

A = lil_matrix((N,N))
B = np.zeros((N,))

for y in range(1,H-1):
    for x in range(1,W-1):
        n = x + y * W
        if x==W//2 and y>H//2: # lightning rod
            A[n, n] = 1.0
            B[n] = 0.0
        else:
            A[n, n] = -4.0
            A[n, (x-1) + y*W] = 1.0
            A[n, (x+1) + y*W] = 1.0
            A[n, x + (y-1)*W] = 1.0
            A[n, x + (y+1)*W] = 1.0
            B[n] = 0.0

for x in range(0,W):
    n = x + 0*W
    A[n,n] = 1.0
    B[n] = 100.0
    n = x + (H-1)*W
    A[n,n] = 1.0
    B[n] = 0.0

for y in range(1,H-1):
    n = 0 + y * W
    A[n, n] = -4.0
    A[n, (W-1) + y * W] = 1.0
    A[n, (0+1) + y * W] = 1.0
    A[n, 0 + (y-1) * W] = 1.0
    A[n, 0 + (y+1) * W] = 1.0
    B[n] = 0.0
    n = (W-1) + y * W
    A[n, n] = -4.0
    A[n, (W-2) + y * W] = 1.0
    A[n, (0  ) + y * W] = 1.0
    A[n, (W-1) + (y-1) * W] = 1.0
    A[n, (W-1) + (y+1) * W] = 1.0
    B[n] = 0.0

A = csc_matrix(A)

PHI = spsolve(A,B)

image = np.zeros((H,W))
for x in range(W):
    for y in range(H):
        val = PHI[x + y*W]
        image[y,x] = val

plt.imshow(image)
plt.colorbar()
plt.show()

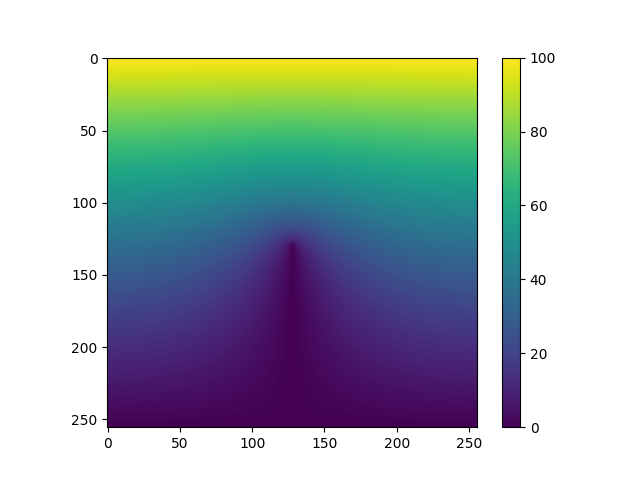
上記のコードの出力結果例が以下である。 確かに中央の避雷針の周囲は比較的遠くまで電位が地上に近く、その勾配もなだらかあることから、落雷が避雷針に誘導されるであろうことが、図からも確かめられる。

避雷針の先端付近では電位の空間変化が大きいので、微分を差分で近似した際の前提が破れてしまっている可能性がある。 そのため、このように空間変化が大きい場所では、マス目の間隔を小さくするなど、計算精度を落とさないための工夫が、実際の現場では、行われている。

　練習： 電場の大きさの表示

上記のコードをもとに、電位（電圧）ではなく、電場の大きさを表示するプログラムを作成しなさい。

ただし、電場の大きさは $$ E = \sqrt{ \left(\frac{\partial \phi}{\partial x}\right)^2 + \left(\frac{\partial \phi}{\partial y}\right)^2 } $$ で与えられる。

　ヒント

　解説: 「雷」のシミュレーション

ラプラス方程式を解く代わりに、ランダムウォークを使うことでも、境界での電場（勾配）の大きさを見積もることができる。

以下は、避雷針の上方からランダム・ウォーカーを放って、避雷針（および放電箇所）や地面に到来したらそこで止めて、「放電箇所」とし、 再び別の場所から放つ操作を繰り返す操作を繰り返すシミュレーションコードの例である。 詳細は割愛するが、ランダム・ウォーカーが到来する確率は、その場所の電場の大きさに比例するので、 確率的な揺らぎを伴いつつ、電場の大きさに比例して、「放電」が生じるようなモデルになっている。

# coding: utf-8

import random
import numpy as np
import matplotlib.pyplot as plt

L=128

def modL(i):
    if i<0:
        return i+L 
    elif i>=L:
        return i-L
    else:
        return i
    

A = np.zeros((L,L),dtype='int')

for j in range(L-1,L//2,-1):
    A[j,L//2]=1

for i in range(L):
    A[L-1,i]=1

htip=L//2

done=False
while not done:
    x = random.randrange(0,L)
    y = htip-2
    redo = False            
    while not redo:
        dx,dy = random.choice([[+1,0],[-1,0],[0,+1],[0,-1]])
        x = modL(x + dx)
        y = y + dy
        if y<=0:
            redo = True
        elif A[y,modL(x+1)]==1 or A[y,modL(x-1)]==1 or A[y-1,x]==1 or A[y+1,x]==1:
            print(x,y,htip)
            A[y,x]=1
            if y<htip:
                htip = y
                if htip<10:
                    done=True
            redo = True
        
plt.imshow(A)
plt.show()

以下は実行結果の例で、避雷針の上方から延びる、稲妻の枝分かれのような構造を確認することができる。 実際の放電現象では、電解の強い箇所に誘電破壊が集中する傾向が一層著しいので、それを反映して、さらに「鋭利」な様相を呈する。