Pythonプログラミング(クラスタリング)
このページは、k-means法によるクラスタリングアルゴリズムについて紹介する。
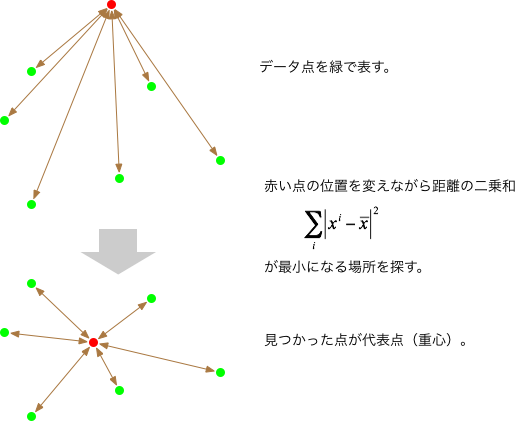
データの代表点
$d$次元空間に多数の点が分布しているとしよう。$i$番目の点の座標を$\boldsymbol{x}^i = (x_1^i, x_2^i, \cdots, x_d^i)$ とする。 これらの点の全体を特徴づける座標の候補となるのが、その平均(重心)で $$ \bar{\boldsymbol{x}} = \frac{1}{N} \sum_{i=1}^N \boldsymbol{x}^i $$ となる。ここで$N$は点の総数である。 平均がデータ点を代表するのはごく自然(自明)な気もするが、以下では改めてその背後にあるモデルについて考えてみよう。
いま、データ点が$d$次元空間にランダムにガウス分布していると想定する。座標 $\boldsymbol{x}$ に点が出現する確率は $$ p(\boldsymbol{x}) = \frac{1}{(2 \pi)^{d/2} \sigma^d} \exp\left( - \frac{\|\boldsymbol{x}- \hat{\boldsymbol{x}}\|^2}{2 \sigma^2} \right) $$ となる(ここで、分布の「中心」を $\hat{\boldsymbol{x}}$、 座標軸毎の分散を$\hat{\sigma}^2$、 $\sum_{j=1}^d (x_j - \hat{x}_j) = \|\boldsymbol{x}- \hat{\boldsymbol{x}}\|^2 $とおいた)。
$N$点から成るデータ $\{\boldsymbol{x}^1, \boldsymbol{x}^2, \cdots, \boldsymbol{x}^N \}$ が与えられているとき、 それらが同一のガウス分布に従いかつ独立であるとの仮定のもとで いちばん尤もらしい $\hat{\boldsymbol{x}}$ と $\hat{\sigma}^2$ は、それらが尤度 $$ p(\boldsymbol{x}^1) p(\boldsymbol{x}^2) \cdots p(\boldsymbol{x}^N) $$ を最大になるような場合である。 ここでは $p(\boldsymbol{x})$ がガウス分布することを仮定しているので、最小二乗法での議論と同様に、尤度が最大になるのは、 $$ \sum_i \|\boldsymbol{x}^i- \hat{\boldsymbol{x}}\|^2 $$ が最小となる場合である。 そこで、その微分を取って $$ \frac{\partial}{\partial \hat{\boldsymbol{x}}} \sum_i \|\boldsymbol{x}^i- \hat{\boldsymbol{x}}\|^2 = - 2 \sum_i \left( \boldsymbol{x}^i- \hat{\boldsymbol{x}} \right) = \boldsymbol{0} $$ から、尤度を最大にするのが重心 $$ \hat{\boldsymbol{x}} = \frac{1}{N} \sum_{i=1}^d \boldsymbol{x}^i $$ であることがわかった。 このように、どの点からも(自乗)平均的に近いような点(重心)を全体の代表とするのは理にかなっているように思える。
複数のデータ点からの距離の二乗和が最小になるような点を探すと、そこが重心(平均)となる。
代表点が異なるデータが混合している場合
次に、確率密度 $$ p_1(\boldsymbol{x}) $$ で分布している点と $$ p_2(\boldsymbol{x}) $$ で分布している点が混じり合っているケースを考えてみよう。
緑の点が確率密度 $p_1(\boldsymbol{x})$ で、青の点が$p_2(\boldsymbol{x})$で、それぞれ分布しているとする。
点の座標のみがデータとして与えられている場合(灰色の点)、どれがどちらの分布から「生成」された点なのかを推定、言い換えれば、 データ点を2つのグループ(クラスタ)に分類する方法を考える。
上では2グループの例を示したが、一般に、グループが$k$個であっても同様である。
$i$番目の点が属するグループを$g(i)$で表すと(例えば、3番目のデータ点が確率密度分布$p_1$から生成されたとすれば、$g(3)=1$、等)、 データ点の独立性を仮定すれば、そのようなデータが得られる尤度は $$ \prod_{i=1}^N p_{g(i)}(\boldsymbol{x}^i) $$ で与えられる。
$p_k(\boldsymbol{x})$がガウス分布で与えられる場合、上記の尤度は、データ点のうちどれだけがどちらのクラスタに属するか(配分数)と、代表点からの二乗和の2つのファクターに影響される: $$ \prod_{i=1}^N \frac{1}{(2 \pi)^{d/2} \sigma_{g(i)}} \exp\left( - \frac{\|\boldsymbol{x}^i- \bar{\boldsymbol{x}}_{g(i)}\|^2}{2 \sigma_{g(i)}^2} \right) $$
対数尤度は $$ L = - \frac{d N}{2} \log(2 \pi) - \sum_i \log(\sigma_{g(i)}) - \sum_i \frac{\|\boldsymbol{x}^i- \bar{\boldsymbol{x}}_{g(i)}\|^2}{2 \sigma_{g(i)}^2} $$ となる。
それぞれのグループの広がり具合(分散 $\sigma_{g(i)}$)の違いが無視できるときは、 対数尤度を最大化するには $$ \sum_{i=1}^N \|\boldsymbol{x}^i- \bar{\boldsymbol{x}}_{g(i)}\|^2 $$ を最小化すれば良いことがわかる。
$k$-means法によるクラスタリング
前節では、代表点(重心)から各点までの隔たりをユークリッド距離 $\|\boldsymbol{x}^i- \bar{\boldsymbol{x}}_{g(i)}\|$ で考慮したが、さらに一般化する余地も考慮して、$\boldsymbol{x}, \boldsymbol{y}$の距離を $$ d(\boldsymbol{x}, \boldsymbol{y} ) $$ と表すことにする。
ここでは、点の分布が$k$個のグループ(クラスター)に分けられることを前提にしよう。 可能な$g(i)$の中から距離の二乗和を最小にする組を見つけるためには、全ての$g(i)$の組み合わせについて調べる距離の二乗和を調べる必要があるが、 データ点の数が増えると膨大な手間となる(データ点が$N$の場合、$k^N$通りの組み合わせとなる)。 そこで、必ずしも最小値が見つかる保証は無いが、少ない手間でそれなりに良い結果が得られるアルゴリズムとして、以下の k-means 法が使われている。
- $k$個の「とりあえずの」代表点(重心)を設定する。
- $S$に「とりあえずの」大きな値をセットしておく。
- データ点$i$に一番近い代表点を探し、$i$をその代表点のグループ割り当てる操作を全ての点について行う。 こうして、割り付けたグループ化の規則を $g(i)$ とする。
- グループ毎の代表点を求める。グループ $\ell$ の代表点は $$ \bar{\boldsymbol{x}}'_{\ell} = \frac{1}{N_\ell} \sum_{g(i)=\ell} \boldsymbol{x}^i $$ ここで、$N_\ell$はグループ$\ell$に属する点の数。
- それに基づいて距離の自乗和 $S$ を計算する: $$ S' = \sum_{i=1}^N d(\boldsymbol{x}^i, \bar{\boldsymbol{x}}'_{g(i)})^2 $$
- もしも $S'\lt S$ ならば、$\bar{\boldsymbol{x}}'$を$\bar{\boldsymbol{x}}$, $S'$を$S$とそれぞれ置き直して、3から繰り返す。 そうでなければ終了する。
上記のアルゴリズムをそのままPythonコードで記述した例を以下に示す:
k-means法によるクラスタリング
sys.float_info.maxはfloat型の最大値。
import sys
import numpy as np
import matplotlib.pyplot as plt
# グループの数
k = 4
# グループ毎の分散
sigma = [[20, 0], [0, 20]]
# データ点の生成
x = np.empty((0,2))
for ell in range(k):
# グループ毎の代表点
pc = np.random.uniform(low=-20, high=20, size=(2,))
xs = np.random.multivariate_normal(pc, sigma,30)
x = np.concatenate([x,xs])
# クラスタリング開始
# 仮の代表点
xc = np.random.normal(0.0, 10.0, (k,2))
s = sys.float_info.max
while True:
g={}
for i in range(x.shape[0]):
d2min=sys.float_info.max
for j in range(k):
d2 = (x[i][0] - xc[j][0])**2 + (x[i][1] - xc[j][1])**2
if d2 < d2min:
d2min=d2
ell = j
g[i]=ell
xc2 = np.zeros((k,2))
n = np.zeros(k)
for i in range(x.shape[0]):
ell = g[i]
xc2[ell][0] += x[i][0]
xc2[ell][1] += x[i][1]
n[ell] += 1.0
for ell in range(k):
if n[ell]>0:
xc2[ell][0] /= n[ell]
xc2[ell][1] /= n[ell]
s2 = 0.0
for i in range(x.shape[0]):
ell = g[i]
d2 = (x[i][0] - xc2[ell][0])**2 + (x[i][1] - xc2[ell][1])**2
s2 = s2 + d2
print("S=",s2)
if s2<s:
xc = xc2
s = s2
else:
break
# 結果のプロット
xdata=[[] for i in range(k)]
ydata=[[] for i in range(k)]
for i in range(x.shape[0]):
ell = g[i]
xdata[ell].append(x[i][0])
ydata[ell].append(x[i][1])
cmap = plt.get_cmap("tab10")
for ell in range(k):
plt.scatter(xdata[ell], ydata[ell], color=cmap(ell))
plt.plot([xc[ell,0]],[xc[ell,1]], marker='+', color='black',markersize=20)
plt.grid(True)
plt.show()
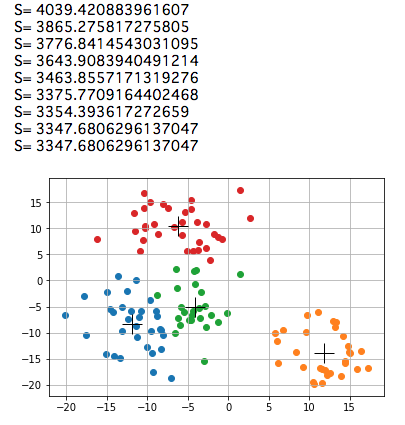
上のコードの実行例
 練習:k-means法の改良
練習:k-means法の改良
データ点のグループ分け(上記のコードでは辞書$g[]$の内容)が決まれば、代表点の位置と代表点からの二乗距離の和はユニークに決まる。 つまり、反復の度に二乗距離の和を計算しなくても、代表点の位置の変化、あるいは、データ点のグループ分けの変化を調べれば、 反復の終了条件が判定できるはずである。
このアイデアに基づいて、上記のコードを「改良」してみなさい。
 練習:k-means法の限界
練習:k-means法の限界
k-means法の発想やアルゴリズムを確認し、意図したようにデータ点がクラスタリングができない可能性があるとすればどんな場合か、考察してみなさい。
 解説:scikit-learnやSciPyの使用
解説:scikit-learnやSciPyの使用
クラスタリングを含む様々なデータ処理を行うためのライブラリとしてscikit-learnやSciPyが広く用いられている。 k-means法によるクラスタリングを、scikit-learnおよびSciPyを用いて行うコードの例を以下に示す:
scikit-learnを使った例
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
# グループの数
k = 4
# グループ毎の分散
sigma = [[20, 0], [0, 20]]
# データ点の生成
x = np.empty((0,2))
for ell in range(k):
# グループ毎の代表点
pc = np.random.uniform(low=-20, high=20, size=(2,))
xs = np.random.multivariate_normal(pc, sigma,30)
x = np.concatenate([x,xs])
# クラスタリング
km = KMeans(n_clusters=k, init='random')
g = km.fit_predict(x)
# 結果のプロット
cmap = plt.get_cmap("tab10")
for ell in range(k):
plt.scatter(x[g==ell,0], x[g==ell,1], color=cmap(ell))
plt.grid(True)
plt.show()
ここでfit_predict(データ配列)は、データが何番目のクラスターに属するかを表す配列を返す。
例えば、0番目のデータがクラスター番号3, 1番目が4, 2番目が0ならば [3,4,0,...] といった具合である。
SciPyを使った例
配列codebookにはクラスターの重心、distortionには重心からの平均距離が返される。
import matplotlib.pyplot as plt
import numpy as np
from scipy.cluster.vq import kmeans
# グループの数
k = 4
# グループ毎の分散
sigma = [[20, 0], [0, 20]]
# データ点の生成
x = np.empty((0,2))
for ell in range(k):
# グループ毎の代表点
pc = np.random.uniform(low=-20, high=20, size=(2,))
xs = np.random.multivariate_normal(pc, sigma,30)
x = np.concatenate([x,xs])
# クラスタリング
codebook,distortion = kmeans(obs=x, k_or_guess=k)
# 結果のプロット
cmap = plt.get_cmap("tab10")
for i in range(x.shape[0]):
plt.scatter(x[i,0], x[i,1], color=cmap(0))
for ell in range(codebook.shape[0]):
plt.scatter(codebook[ell,0], codebook[ell,1], color=cmap(ell+1))
plt.grid(True)
plt.show()
 解説: 高次元のガウス分布
解説: 高次元のガウス分布
ここでは簡単のため、各座標軸毎の分散を等しく$\sigma^2$と仮定している。 こうして構成された$d$次元のガウス分布の分散は、$\sigma^2 \, d$ である。
なお、右の$p(r)$で$\sigma=1$の場合、$r^2=y$と置き直せば、$y$についてのカイ二乗分布に他ならない。
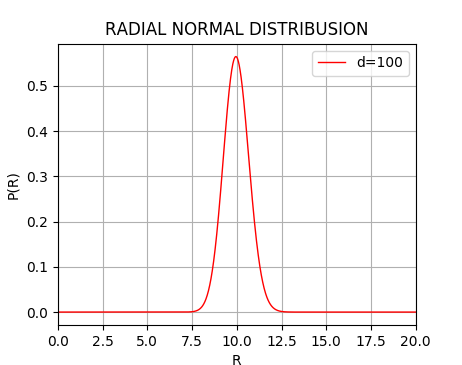
$d$次元の、原点を中心としたベクトル $(x_1, x_2, \cdots, x_d)$の長さを $$ r = \sqrt{ \sum_i (x_i)^2 } $$ とおく。 もし点$(x_1, x_2, \cdots, x_d)$が原点を中心としたガウス分布(各座標変数毎の分散 $\sigma^2$)に従って散らばっているとすると、 $r$についての点の分布密度 $p(r)$ は $$ p(r) dr = \frac{2}{(2 \sigma^2)^{d/2} \Gamma(d/2)} \exp\left( - \frac{r^2}{2\sigma^2} \right) r^{d-1} dr $$ となる。 この $p(r)$は、1次元の場合はよく知られたベル型(の半分)の形となるが、次元が大きくなるにつれて、原点からは離れた位置にピークを持つような形になる (このことは別段ミステリアスではなく、空間次元が高くなると、相対的に原点から距離を置いた点の割合が増えるというだけであって、「ドーナツ」のように原点付近の密度が疎になるわけではない)。
言い換えれば、高次元のデータがガウス分布していると仮定することは、それぞれのデータ点が重心からほぼ等距離の超球面上に分布することを暗に前提(期待)していることに他ならない。
100次元空間でのガウス分布の動径分布をプロットするコードと実行結果の例。 標準偏差(10)の付近に分布が集中することが判る。
# coding:utf-8
import matplotlib.pyplot as plt
import numpy as np
import math
sigma=1
dim=100
rdata = np.arange(0,20,0.01)
n = rdata.shape[0]
pr = np.empty(n)
for i in range(n):
r = rdata[i]
pr[i] = 2/((2*sigma**2)**(dim/2) * math.gamma(dim/2)) * math.exp(-r**2/(2*sigma**2)) * r**(dim-1)
plt.title("RADIAL NORMAL DISTRIBUSION")
plt.plot(rdata,pr, color=(1.0,0,0.0), linewidth=1.0,label="d="+str(dim))
plt.xlim(0,20)
plt.xlabel('R')
plt.ylabel('P(R)')
plt.legend()
plt.grid(True)
plt.show()