情報基礎A 「Cプログラミング」（ステップ４・ニュートン法）

このページは、方程式の数値解を反復によって求める方法について考える。

１．反復によって方程式を解く

二次方程式 $x^2 - x - 1 =0$ の解を求める方法について考えてみよう。もちろん我々は解の公式を知っているので、直ちに $$ x = \frac{1 \pm \sqrt{5}}{2} $$ で一件落着なのだが、仮に、解の公式を知らず、しかも、数値的に値が求まれば十分、といったケースをここでは想定する。 事実、世の中には「解の公式」が無い（まだ見つかっていない、仮に見つかったとして複雑すぎて使えない、あるいは、公式そのものが存在しない）場合がほとんどである。

まず、元々の方程式を少し変形して $$ x = 1 + \frac{1}{x} $$ と書き直してみる。そして、その右辺と左辺をそれぞれ $x$ の関数だと思ってプロットすると、以下のようになる（茶色が$x$、青が$1+1/x$)。

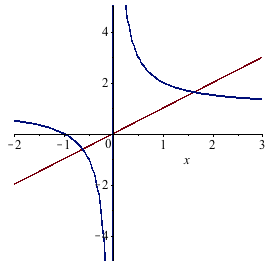
c-4-sup-quad-eq-solution

このとき、二つの線の交点の $x$ の値を求めることができれば、方程式が解けたことになる。

このような方法は一般に反復法と呼ばれ、実用的な数値計算のアルゴリズムのかなりは、反復法に分類できる。

その計算法は案外と単純である：

  1. $x$の出発値をセットする
  2. $x^\prime \leftarrow 1 + 1/x$
  3. 値の変化量 $\left| x^\prime - x \right|$ が十分小さい値になれば反復を終了し、5に進む
  4. $x^\prime$ を改めて $x$とおいて、2からを繰り返す
  5. 解として $x^\prime$ を出力し、終了する

実は、このパターンの計算はすでに登場していて、連分数

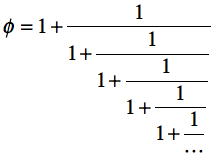
c-4-eq-cont-frac-golden-ratio

の例題プログラム4bが、まさに「これ」である。

ここで、注意深い諸君は、上の計算では二次方程式の２つの解のどちらが求まるのか（あるいは両方求まるのか）が気になるだろう。 それについて考えるため、「まず $x$ の出発値を選んでおいてから、$1+1/x$ を新しい $x$ だと考えて繰り返す」というプロセスを図で表してみたのが以下である。 波線は　出発値のセット、矢印付きの線分は反復を表している。 図の左側では反復の度に交点から遠ざかる一方で、右側では値が交点に収束するように見える。

$y=1+1/x$ の $y$ の高さが $x^\prime$ に対応するので、 そこから水平線を横に伸ばして、$y=x$ との交点の位置を求め、 その点での $x$ の値を次の計算ステップの出発値 にすれば、 $x \leftarrow x^\prime$ とおいて、次の反復へと進んだことになる。

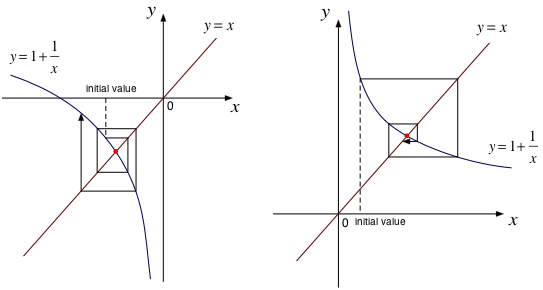
c-4-iteration-sup-quad-eq-fixed-points

つまり、上記の計算法によって求めることができるのは、解のうち片方（図で右側の$(1 + \sqrt{5})/2$)だけなのだ。

この違いは、交点 $x=x^*$ での関数 $y(x)=1+1/x$ の傾きの大きさによって決まり、（以下で述べるように）$\left| y'(x^*) \right| < 1$ であれば、値が交点（固定点と呼ぶ）に収束することがわかる。

この方法はエレガントさは欠くものの、力業で結果を得たい場合には、案外と便利である。

以上で述べた方程式を解くための手順を、もう少し一般化してまとめると、

となる。

* ということは、$x=y(x)$ のパターンの作り方を工夫することで、別の解まで探し出すことができる可能性がある。 例えば、上の二次方程式の例では、$z=1/x$ と変数変換してから、$z \leftarrow 1/z - 1$ を反復すると、他方の解を得ることができる。

icon-pc　練習：非線形方程式の数値解

反復法を使って、非線形方程式 $\exp(-x) - \frac{x}{x+1}=0$ の解を求めるプログラムを作成し、動作を確認せよ。

icon-hint　ヒント

解は $x=-1.349976485 \cdots$ 、および $x= 0.8064659942\cdots$ である。

icon-teacher　解説 : 固定点の安定性

解くべき方程式 $x=y(x)$ を見ると、これは、関数 $y(x)$ の値が再び $x$ になっている状態を探すことに他ならず、 そのような $x=x^*$ は $y(x)$ の固定点(fixed point)と呼ばれる。 いま、反復の過程で、固定点の近くの $x=x^* + \delta$ の状態にあったとすると、次の反復では、値は $y(x^* + \delta)$ に更新される。 固定点の周りで $y(x)$ を展開し、$y(x^*)=x^*$ であることを思い出して、式を整理すると $$ y(x^* + \delta) = x^* + y'(x^*) \delta + O(\delta^2) $$ となる。これは、最初の「ずれ」$\delta$が、反復の過程で（高次の項が無視できるような状況では） $$ \delta \to y'(x^*) \delta $$ と変換されることに対応する。つまり、$n$回の反復で、「ずれ」は $(y'(x^*))^n \delta$ のように変化することになるので、 それが$0$に収束するための条件（あるいは、固定点が安定である条件）は $\left| y'(x^*) \right| < 1$ となる。


２．ニュートン法による求根

ここで、再び $x^2 - x - 1 = 0$ の数値解法を考えよう。 $f(x)=x^2-x-1$ とおいて、$y=f(x)$ をプロットすると下図のようになるが、x軸とグラフの交点の位置を我々は求めたいわけである。

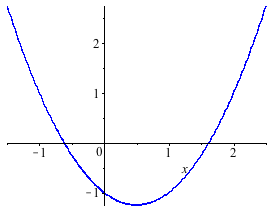
c-4-sup-quad-eq-newton1

この種の問題に対しては、ニュートン法（Newton's method)と呼ばれる、非常に効率のよい反復法のアルゴリズムが知られている。 その計算手順はそれほど難しいものではない：

ニュートン法

  1. $x$ の出発値をセットする
  2. その位置で $y=f(x)$ の接線を引き、接線がx軸と交叉する点の $x^\prime$ の値を求める
  3. 値の変化量 $\left| x^\prime - x \right|$ が十分小さい値になれば反復を終了し、5に進む
  4. $x^\prime$ を改めて $x$とおいて、2からを繰り返す
  5. 解として $x^\prime$ を出力し、終了する

ここで、より具体的な計算手順を得るために、$n$ 回目の反復の際の $x$ の値を $x_n$ と置いて、反復の過程を考えてみよう。 まず、ステップ２〜４の反復の様子を図で表すと、次のようになる。赤線が接線である。

ニュートン法は、単純な反復法に較べ、格段に収束が速く、１回の反復あたり、精度（有効桁数）が倍になることが知られている。

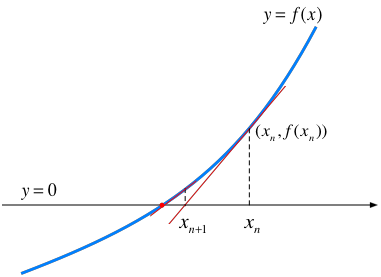
c-4-sup-quad-eq-newton2

ここで、座標 $(x_n,f(x_n))$ を通り、勾配が $f'(x_n)$ の直線の方程式は $$ y = f'(x_n) (x - x_n) + f(x_n) $$ であるから、この式で $y=0$ とおいて、$x$ について解くと、 $$ x = x_n - \frac{f(x_n)}{f'(x_n)} $$ となる。この値を、次のステップの$x$とするわけだから、ニュートン法の反復の「ステップ２」では、 $$ x_{n+1} \leftarrow x_n - \frac{f(x_n)}{f'(x_n)} $$ という処理を行えばよいことが分かった。

例えば、$f(x)=x^2-x-1$ の場合、その導関数は $f'(x)=2x-1$ とすぐ計算できるので、具体的なCのコードは以下のようになるだろう：

例題4c (ex4c.c)

出発値を適切に選ぶことによって、方程式の二つの解がそれぞれ計算できる。 

#include <stdio.h>
#include <math.h>

main()
{
  float x,xp ;
  printf("出発値:") ;
  scanf("%f",&x) ;
  for(;;) {
    xp = x - (x*x-x-1)/(2*x-1) ;
    if (fabs(xp-x)<0.00001) break ;
    x = xp ;
  }
  printf("x= %f\n",xp) ;
}

電卓やパソコンで $a$ の平方根を求める際には $f(x)=x^2-a$ とおいて、実際に、内部でニュートン法による計算処理が行われている。

icon-pc　練習：ニュートン法

ニュートン法を使って、非線形方程式 $\exp(-x) - \frac{x}{x+1}=0$ の解を求めるプログラムを作成し、動作を確認せよ。

icon-teacher　解説 : ニュートン法の収束性

ニュートン法で $f(x)=0$ の数値解を計算する際、$n$回目の反復を行なった時点で、解 $x^*$ からまだ $\delta$ だけずれていた、すなわち、 $$ x_n = x^* + \delta $$ であったとしよう。

この状態で、さらに反復を続けると、次のステップでは $$ x_{n+1} = x^* + \delta - \frac{f(x^* + \delta)}{f'(x^* + \delta)} $$ となるが、関数を$x^*$の周りでテイラー展開 $$ f(x^*+\delta) = f(x^*) + f'(x^*) \delta + \frac{1}{2} f''(x^*)\delta^2 + O(\delta^3), \\ f'(x^*+\delta) = f'(x^*) + f''(x^*) \delta + O(\delta^2) $$ して、定義から $f(x^*)=0$ であることを思い出しながら、式を整理すると $$ x_{n+1} = x^* + \frac{1}{2} \frac{f''(x^*)}{f'(x^*)} \delta^2 + O(\delta^3) $$ となる（$\delta$の一乗の項は相殺されて消えるところがミソである）。

この性質を2次収束(quadratic convergence)という。

$\delta$の「減り具合」の式からは、$f(x)=0$ が重根を持つような場合（$f'(x^*)=0$）、 ニュートン法はうまく働かないことも予想できる。

つまり、テイラー展開で $\delta$ の3次以上の項が無視できるくらいに $|\delta|$ が十分小さければ、1回の反復によって、誤差が $\delta$の２乗に依存して、 $$ \delta \to \frac{1}{2} \frac{f''(x^*)}{f'(x^*)} \delta^2 $$ のように変化することになる。 このことは（感覚的には）誤差が $1/10 \to 1/100 \to 1/10000 \to \cdots$ と急激に減少することを意味している。


tfield-icon亀場で練習：反復写像

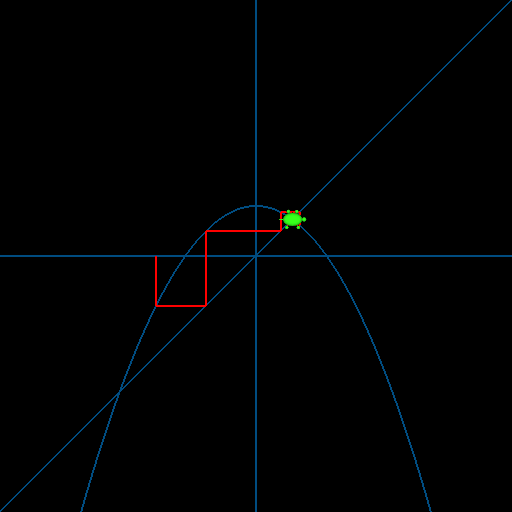
$x$ の方程式 $x^2/100 +x-C = 0$ の解をこのページで説明した反復法で解こうと考え、$y(x)=-x^2/100+C$ とおいた。 下図は、$C=50$ の場合に、$x$の出発値を-100とおいて反復計算を行った過程を亀場を使って表示した例である。

これと同様にして、反復を亀の軌跡によって可視化するプログラムを作成してみよ。さらに、$C$ の値を色々と変え、亀の挙動を観察してみよ（例えば$C=150$）。

c-4-tfield-logistic-map