情報基礎A 「Cプログラミング」(ステップ8・ソーティング)
配列の応用として、データの整列(ソーティング)について、すでに取り上げた。 データの件数が多くなると、整列により時間がかかるのは当然であるが、問題は、その遅くなり方である。 ここでは、データ件数が増えても実用的な、ふたつのアルゴリズムを、再帰的な関数の応用例として、紹介する。(ここは書きかけ)
1.作業を小分けにしてゆく:クイックソート
ソーティングの中で、一番簡単な問題は、要素がひとつだけの配列の並べ替えで、配列$\{a\}$ を並べ替えた結果は $\{a\}$である。
次に簡単なのは、$\{a, b\}$ の並べ替えで、例えば昇順に整列する場合、$a \le b$ であったら、$\{a, b\}$、そうでなければ $\{b, a\}$を結果とすれば良い。
ここで、$a, b$ が配列の場合($a = \{a_1, \cdots, a_n\}, \, b = \{b_1, \cdots, b_m\}$)に、上の議論を拡張してみよう。 そして、$\{a_1, \cdots, a_n\} \le \{b_1, \cdots, b_m\}$とは、全ての要素のペアについて $a_i \le b_j$ が成り立つこと、と定義する。
次に、ある配列 $x = \{x_1, \cdots, x_n\}$ が与えられたとき、それを、$a \le b$ であるようなふたつの配列 $a,b$ に分解する方法を考えてみよう。 集合論の記号を使えば、$a \subseteq x, \,\, b \subseteq x$ であって、かつ、共通要素が無い、つまり $a \cap b = \varnothing$ とする。 例えば、$\{ 3, 1, 7, 2, 5\}$ を $\{3, 1, 2\}$ と $\{7, 5\}$ に分割する手順をどう与えるか、という意味である。 この定義からは、配列に同じ要素が複数含まれている場合、分割の方法は (重複する要素の数)-1 通り存在することになる。
配列を大小ふたつの部分配列に分割するには、ある参照値を決めて、それより小さいグループと大きいグループに選別すればよい。 この参照値はピボット(pivot)と呼ばれている。
ピボットの選び方は大切である。 なぜなら、もし、配列中の最大値以上の数や最小値以下の数を選んでしまうと、片側の配列が「空」になってしまう場合が生じる。 つまり、分割したはずなのに、分割されていない、という状況が生まれてしまうからである。 実用上よく使われるのは、配列の中からいくつか要素をピックアップして、その平均値をピボットとする、という方法である。 そうすれば、よほど運が悪く無い限り、ピボットが極端な値となることは無いはずだ。
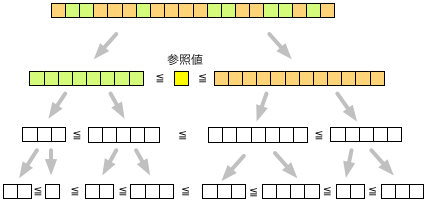
こうして、長い配列 $x$ が、$a \le b$ となるような2つの配列に分解できたとしよう。 そして、さらに $a, b$ も同様に分解して・・・という操作を繰り返していけば、いずれ、要素が1つだけの配列になる。 そのとき、その部分列の整列作業は完了し、かつ、分解されたそれぞれの配列の大小関係も、昇順に揃っているはずである(下図)。
C言語の標準ライブラリ関数には、クィックソートでデータ列をソートする関数(qsort()等)が含まれている。
通常のプログラミングでは、その関数を呼び出せば事足りる場合がほとんどである。
このように、配列を、要素の値の大小によって2つのグループに分割する操作を繰り返し、全体を整列させるアルゴリズムはクイックソート(quicksort)と呼ばれ、その名のとおり、高速な整列アルゴリズムの定番である。
要素数$n$の配列を、半分ずつに分けて、要素数1にまで分解するには、何ステップ必要だろうか。分割が順調に行けば、1ステップあたり部分配列の数は倍ずつ「ねずみ算」式に増えるから、$m$ステップ後には$2^m$個の配列に分解される。 それが全要素数より大きくなればよい($2^m \ge n$)のだから、$m \ge \log_2 n$、つまり、$\log_2 n$ ステップは最低でも必要である。 それら各ステップで要素の入れ替えが $n$ 回程度必要になるので、ソーティング全体としては $n \log_2 n$ 回程度の入れ替えの手間が発生する(計算量$O(n \log n)$)。 バブルソートや選択ソートの計算量$O(n^2)$と較べ、$n$が大きくなると、これは著しい改善となる。
ただし、上記は分割が順調に行われた場合で、長さ $n$ の配列が長さ $1$ と $n-1$ のように分解される状況では「ねずみ算」にはならず、計算量は、最悪で$O(n^2)$になってしまう可能性がある。
配列の分割の具体的な手順
配列の分割を行なう際、データの臨時置き場が必要となるようではメモリー効率が悪いので、ひとつの配列の前半部分にはピボット以下の要素が、後半にはピボットより大きな要素は配されるよう、並べ替えを行なう。そのとき、前半部と後半部それぞれの中では、データの大小関係はでたらめで構わない。
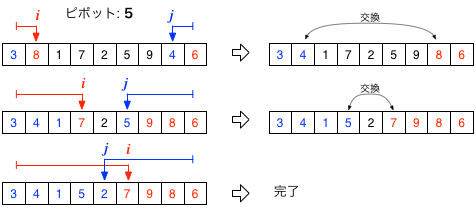
そこで、下図のように、配列の先頭から後方に向かって「動く」変数 $i$ と、後方から前方に向かう変数 $j$ を用意する。 $i$ が指す場所の値がピボットより大きく、$j$ が指す場所がピボット以下なら、$i$と$j$の場所の値を交換しながら、$i$と$j$の大小関係が逆転するまでこれを続けたとしよう。すると、最終的に、$j$以下の場所にはピボット以下の要素、$i$以上の場所にはピボットより大きな要素が並んでいるはずである。
配列の中(in-place)で、値の大小に応じて、ふたつのグループに仕分けを進める例。 この場合のピボットは5。 二つの変数を使って「挟み撃ち」にしている。
クィックソートのコーディングの例
以上のアイデアを元に、配列x[]のfirst番目からlast番目までの区間をソートする関数をCでコーディングした例を示す:
右の例では、まず最初の要素をピボットに設定してみて、分割後、片方が空になっていたら(つまり、分割されていなければ)、 2番目の要素をピボットにし直して、再度分割を試みる・・・、を繰り返すようにプログラムされている。 分割できなければ、全ての要素が同じ値ということなので、ソーティングをそこで止めにする。
void quick_sort(int first, int last, float x[])
{
int i,j,ip ;
float pv,w ;
if (first==last) return ;
ip=first ;
do {
pv=x[ip] ;
i=first ;
j=last ;
for (;;) {
for ( ; i<=last && x[i]<=pv ; i=i+1) ;
for ( ; j>=first && x[j]>pv ; j=j-1) ;
if (i<j) {
w = x[i] ;
x[i] = x[j] ;
x[j] = w ;
} else break ;
}
ip=ip+1 ;
} while (ip<=last && j==last) ;
if (ip>last) return ;
quick_sort(first,j,x) ;
quick_sort(i,last,x) ;
}
 練習:クイックソート
練習:クイックソート
上記の関数の設計を参考に、クイックソートで昇順に配列を整列するCプログラムを完成させ、動作を確認しなさい。
さらに、上記のコードを手直しして、クィックソートで降順に整列するプログラムを作成しなさい。
2.ボトムアップなアプローチ:マージソート
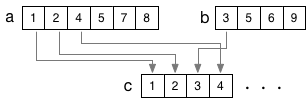
すでに整列済みの2つの配列 $\{a_i\}$ $(i=1,\cdots,n)$ と $\{b_j\}$ $(j=1,\cdots,m)$ が用意されていたとする。 それらを元にすれば、2つの配列を併合(merge)して、整列された配列 $\{ c_k \}$ $(k=1,\cdots,n+m)$ を容易に生成することができる。
具体的には、配列 $a$ と $b$ の先頭から、順にデータを読み、大小を比較して、小さいほうを $c$の末尾に追加していく作業を繰り返せばよい。 配列の最後まで 読み込んだら、その配列の読み込みはそこで止め、まだ読み込みが終わっていないほうの配列の残りの部分をさらに$c$に加える。 こうして、全てのデータを$c$に「転写」したら、作業は完了である。 併合の際、$a$と$b$の(読み出しを終えていない箇所の)先頭のみを比較し・取り出せば良いので、その手間(処理回数)は、配列の要素数程度である。
並べ替えたいデータが、予め、小さな破片に分割されていたとする。すると、上記の手続きを、全体が1つの配列に併合されるまで繰り返して適用すると、最終的に得られる配列の内容は、きちんと整列されているはずである。 その様子を図に示す:
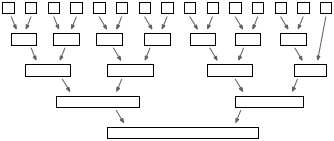
このように、分割と併合を組み合わせてデータを整列するアルゴリズムは併合ソート(マージソート: merge sort)と呼ばれ、高速で性質が良いことが知られており、実用上も重要である。
クイックソートがトップダウン的なアプローチとすれば、マージソートは、ボトムアップ的な手法と言うことができるだろう。
ここでは、マージソートによって配列を並べ替える関数 merge_sort() を設計してみよう:
関数 merge_sort(配列 $\{x_i\}$ の $first$ 要素目から, $last$ 要素目までを整列):
もし $first = last$ なら、整列は必要ないので、その区間の処理は完了
$first \le m \lt last$ であるような中間点 $m$ を決める
2つの部分区間 $[first, \ m]$, $[m+1, \ last]$ それぞれについて、merge_sort()を行なう
整列済みとなった2つの部分区間 $[first, \ m]$, $[m+1, \ last]$ のデータを併合する
これをCの関数としてコーディングした例を示す:
void merge_sort(int first, int last, float x[], float w[])
{
int m ;
if (first==last) return ;
m = (first + last)/2 ;
merge_sort(first,m,x,w) ; merge_sort(m+1,last,x,w) ;
perform_merge(first, m, m+1, last, x, w) ;
}
特別な工夫を凝らさない限り、マージソートでは併合の際に作業用の記憶領域が必要となる。
ここで、配列 w[ ]は、併合の際のデータの「仮置き場」である。
関数の中で、分割した2つの区間の併合を行なうために、さらに別の関数perform_merge()を呼び出している。
そちらをコーディングした例を以下に示す:
void perform_merge(int i1, int i2, int j1, int j2, float x[], float w[])
{
int i,j,k ;
k = i1 ;
i=i1 ; j=j1 ;
for (;;) {
if (i<=i2 && (j>j2 || x[i] <= x[j])) {
w[k] = x[i] ;
i=i+1 ;
} else if (j<=j2 && (i>i2 || x[i] > x[j])) {
w[k] = x[j] ;
j=j+1 ;
} else break ;
k=k+1 ;
}
for (k=i1 ; k<=j2; k=k+1) {
x[k] = w[k] ;
}
}
 練習:マージソート
練習:マージソート
上記の関数の設計を参考に、マージソートで昇順に配列を整列するCプログラムを完成させ、動作を確認しなさい。
さらに、上記のコードを手直しして、マージソートで降順に整列するプログラムを作成しなさい。
3.分割統治アルゴリズム
このページに登場したふたつのアルゴリズム(クイックソートとマージソート)は、いずれも、問題をより規模の小さな問題に分割し、 それぞれの結果を統合して大きな問題を解く、というアプローチで組み立てられている。 このようなアルゴリズムは分割統治アルゴリズム(divide and conquer algorithms) と呼ばれ、ソーティングに限らず、いくつもの実用的で重要な応用例が知られている。
大きな問題が与えられた際、それを小さな問題に分解してみてはどうか、とは誰でも思いつくだろうが、分割統治が上手く働くためには、問題を分割するだけでは不十分で、分割によって生じた部分同士がお互いに依存し合わないようになっていなければならない。 例えば、クィックソートの過程で、生成した部分列内の整列はその部分列の中だけで関係しており、別の部分列の状態は全く処理に関係しない。 マージソートでも、併合は二つの部分列の間だけで行なわれる。 加えて、問題の大小に関わらず、必要な手続きが全く同様(あるいは、「相似」)であれば、以下のように、再帰によって簡潔にそのアルゴリズムを記述できる:
データ $x$ が、いくつかの部分 $\{x_i\}$ に分解することができ、それぞれの「小問題」についての結果(解)が $f(x_i)$ で与えられるとしよう。 さらに、$x$ に対する結果が、部分のそれから「合成」できる、すなわち、$f(x) = g\left(\{ f(x_i) \}\right)$ となるような手続き $g$ が与えられるとき、 「関数」$f$ は、形式的に、
1: 関数 $f(x)$ :
2: $x$ が十分小さいサイズならば「正攻法」で求めた解(又は、自明な解)を返す
3: そうでなければ:
4: $x$ を分割して $\{x_1, \cdots, x_n\}$ を得る
5: $f(x_1), \cdots, f(x_n)$ を計算する
6: $g(\{ f(x_i) \})$を解として返す
によって再帰的に定義できる。
 練習:分割統治アルゴリズムとしてのソーティング
練習:分割統治アルゴリズムとしてのソーティング
このページで示したクィックソートとマージソートのC関数の例を読み、上記の分割統治の形式的な関数定義との対応関係(Cのコードのどの箇所が、形式的な定義の何行目と対応しているか、および、$\{x_i\}$は何に相当しているか)を示せ。