亀場でプログラミング:迷路探索
(ここは書きかけ)
このページでは、亀に迷路を探索させる方法について考察してみたい。
亀場関係のソフトウェアについてのさらに詳しい説明は
亀場サーバー操作マニュアル
を参照のこと。
亀場の上でキーボードの大文字M(シフトm)を押すと迷路モードになる
1. 亀場を迷路にする
亀場サーバーのウィンドウをクリックして前面に出した状態で、半角の大文字 M をタイプすると、亀場の上に毎回異なる迷路が作成される。 もう一度Mを押すと、迷路は消える。 このとき、亀は一旦綺麗に消されて(殺されて)しまう。 画面に迷路が表示されている状態を「迷路モード」とでも呼ぶことにしよう。
迷路モードに入ると、画面の中央に、ドーナッツが4つ、出現する。 この状態で亀場に(CやRubyのプログラムによって)接続すると、亀は画面の左下に現れるようになっている。 そして、プログラミングの目標は、「できるだけ効率よく迷路を通り抜けて、これらのドーナッツをゲットする(砲撃して命中させる)こと」にある。

迷路の壁はもちろん通り抜けることはできないし、砲撃しても、壊れることも決してない。
2. 迷路を抜けるためのアルゴリズムを考える
ループのない迷路を探索する基本的なアルゴリズムとしてよく知られている「右手法(wall follower)」から、まず検討してみよう。 右手法は極めて単純で、迷路の壁を右手でいつも触りながら進めば、いつかは出口に出られる、というものだ。 ただし、迷路が単連結(simply connected)になっていなければならない。 残念ながら亀場が生成する迷路は必ずしも単連結であるとは限らないが、一番単純なアルゴリズムとして、まず、右手法から試してみよう。
右手法をプログラムとして実装するには、亀の右側と前方に障害物があるかどうかをチェックするセンサーが必要だ。 そしてもし、そうしたセンサーが使えるとしたら、亀に迷路を歩かせるための行動プログラムの骨格は
以下を繰り返す 右側と前方にそれぞれ壁があるかどうかをチェックする もし右側が空いていたら、右に曲がる もし右が塞がっていて、かつ、前が空いていたら、直進する それ以外なら(右も前も塞がっていたら)、左に曲がる |
となるはずだ。これをCのプログラムとして表現するためには、「右側と前方に壁があるかどうかチェックする」機能が 必要となるが、我々の亀は案外賢くて、そのためのセンサー(sonar)を備えている。
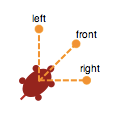
ソナーは、斜め45°左前方、正面、そして斜め45°右前方の、20ピクセルの範囲に障害物があるかどうかを検出するセンサーである。 ただし、FINDERのように障害物の種類を区別したり、到達距離を調整したりすることはできない。
このソナーを使って、上記のアルゴリズムをもうちょっとC言語らしく表現すると、以下のようになる:
int left,front,right ;
...
while(1) {
Q_SONAR(&left,&front,&rignt) ;
if (right==0) { 右に曲がる ;}
else if (right==1 && front==0) { 直進する; }
else { 左に曲がる; }
}
|
 練習:右手法による迷路の探索
練習:右手法による迷路の探索
上で述べた右手法をCプログラムとして実装し、実際に亀が迷路の中を歩き回れるようにしなさい。
 ヒント
ヒント
迷路のコーナーをくるりと回るには、それなりに曲率が大きくなければならないので、 回転角と前進のステップには、それなりのさじ加減が必要。
プログラムの骨格はすでに示した通りなので、「右に曲がる」、「直進する」、「左に曲がる」のところをさじ加減(回転角度、移動量)を調整する のが主な作業となる。 その際、例えば、「右に曲がる」=「右にちょっと曲がって、ちょっと進む」という風にプログラムすると、動きがなめらかになって、 角地で引っかかりにくくなるかもしれない。
上記のアルゴリズムは、いつも壁が近くにあることを前提にしている。 もし、周囲に壁が無ければ、亀は右に回転しつづけることになるだろう(いつもright==0だから)。 偶然、亀が迷路の壁と壁の中間辺りに来ると、実際に、こういう状況に陥る場合がある。 それを回避するには、「右に回りつづけたら、回転せずに壁に達するまで直進する」といった行動プログラムも 付加しておくとよい。
 練習:ドーナッツをゲット
練習:ドーナッツをゲット
上の課題プログラムに、「ドーナッツが見つかったら砲弾を発射する」という行動を追加し、ミッションが達成できるようにしなさい。
3. 全探索を行う
右手法はアルゴリズムの単純さと引き替えに、ループに遭遇すると、同じ場所をぐるぐると回ってしまって、 「先」に進むことができなくなるという難点がある。 それを克服するため、バックトラッキングアルゴリズムの 一種である深さ優先探索アルゴリズムを使って、 迷路を16×16のマス目に区切った場合に、それらの全ての場所を探索できるように工夫したプログラムの例を以下に示す。
プログラム中、search_path(i0, j0, i1, j1)という関数が探索を行っている。関数の引数 i1, j1 が、現在探査中の区画の位置を、 i0, j0が1ステップ前に調べた区画の位置を、それぞれ表しており、この関数の中では以下の処理を行っている:
- 現在訪れた区画に、「訪問済み」の印をつける(下図の赤丸)。
- 隣接する上下左右の区画を調べ、すでに訪問済みではなく、かつ、途中に壁の無い(到達可能な)区画が見つかったら、その区画に移動して、同じ手順を繰り返す。
- 探索が終わったら、1ステップ前の区画に戻る(図の水色の矢印)。
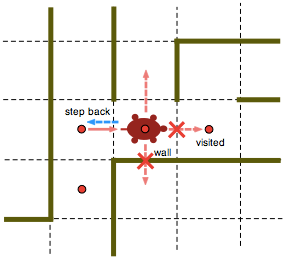
迷路の全探索を行い、ドーナッツがあったら砲撃するプログラムの例。
実行する前に、亀場サーバーのウィンドウ上で M キーを押して、迷路を作成しておくこと。
左下隅の区画を出発したカメは、到達可能な場所を全て訪れ、最後に、左下隅に再び戻ったところでプログラムは終了する。
二次元配列 map[ ][ ]:訪問済みの区画に印をつけるために用いる
set_heading_to(角度):カメの頭を角度の方向に向ける
mov_to_section(i, j):カメを、区画(i, j)に移動する
can_step_forward(角度):現在地からみて、角度の方向に進行可能かどうかチェックする
search_path(i0, j0, i1, j1):区画(i0, j0)からその隣の区画(i1, j1)に進んだ際に、さらにその先の経路を調べる
#include <stdio.h>
#include <math.h>
#include "turtle.h"
#define NDIV 16
#define SQR(x) ((x)*(x))
int map[NDIV][NDIV] ;
void init_map() {
int i,j ;
for (i=0; i<NDIV; i++)
for (j=0; j<NDIV; j++)
map[i][j] = 0 ;
}
void set_heading_to(float angle) {
float a ;
Q_DIR(&a) ;
if (angle-a>180) angle-=360 ;
else if (angle-a<-180) angle += 360 ;
do {
Q_DIR(&a) ;
LT(angle-a) ;
} while (fabs(angle-a)>0.001) ;
}
void mov_to_section(int i, int j) {
float goalx = 32.0*(i-8) + 16.0 ;
float goaly = 32.0*(j-8) + 16.0 ;
float curx,cury,dir,dist ;
Q_POS(&curx,&cury) ;
dir = atan2(goaly-cury,goalx-curx)*180.0/M_PI ;
set_heading_to(dir) ;
do {
Q_POS(&curx,&cury) ;
dist = sqrt(SQR(curx-goalx)+SQR(cury-goaly)) ;
FD(dist) ;
} while (dist>0.001) ;
}
int can_step_forward(float angle) {
int res ;
set_heading_to(angle) ;
RF(32.0) ;
Q_FINDER(&res) ;
if (res==0) return 1 ;
else if (res==2) {
FIRE() ;
IDLE(0.5) ;
return 1 ;
} else return 0 ;
}
int search_path(int i0, int j0, int i1, int j1) {
map[i1][j1]++ ;
if (i1+1<NDIV && map[i1+1][j1]==0 && can_step_forward(0.0)) {
mov_to_section(i1+1,j1) ;
search_path(i1,j1,i1+1,j1) ;
}
if (i1-1>=0 && map[i1-1][j1]==0 && can_step_forward(180.0)) {
mov_to_section(i1-1,j1) ;
search_path(i1,j1,i1-1,j1) ;
}
if (j1+1<NDIV && map[i1][j1+1]==0 && can_step_forward(90.0)) {
mov_to_section(i1,j1+1) ;
search_path(i1,j1,i1,j1+1) ;
}
if (j1-1>=0 && map[i1][j1-1]==0 && can_step_forward(-90.0)) {
mov_to_section(i1,j1-1) ;
search_path(i1,j1,i1,j1-1) ;
}
mov_to_section(i0, j0) ;
}
main()
{
CON("localhost") ;
NM("kame") ;
BMODE() ;
PD() ;
init_map() ;
mov_to_section(0,0) ;
search_path(0, 0, 0, 0) ;
}
 練習:コイン並べ
練習:コイン並べ
上のプログラムを元にして、下図のように、迷路の全ての区画にコインを1枚ずつ並べるプログラムに改造しなさい。ただし、同じ区画内にコインを2枚以上置かないこと。

 ヒント:
ヒント:
最初にカメはコインを持っていないので、最初にBORROWCOIN()を26回呼び出して、260枚のコインを得ておく(必要な枚数=16X16区画=256 < 260)。 DROPCOIN( )を呼び出すと、現在位置にコインが1枚置かれる。