Pythonプログラミング（モンテカルロ・シミュレーション）

「群れ」のシミュレーション

このページでは、抽象化された「群れ」の集団的な挙動のモデルとそのシミュレーションについて考える。

「群れ」を単純化したモデル

鳥や魚の群れや、顕微鏡下で動き回る細胞の集団まで、沢山の動物がひしめき合って動いているを我々はよく目にする。我々ヒトとて例外ではなく、駅や通路で歩いている人混みの様子を眺めていると、牧羊犬に導かれて行進する羊の群れとの間に本質的な違いはあるのだろうか、と、問いたくなることもある。

こうした群れの中での個体の動き方をとことん抽象化すると、以下のように要約することも可能であろう：

だいたい一定の速度で前進し続けている
近くの個体の運動方向に近い向きに進もうとする
しかしながら、完全に向きを揃えるわけでもなく、ばらつきもある

向きを揃える効果が大きければ、軍隊の行進のように、全体として同じ方向揃って運動するようになるように想像されるが、実際のところはどうなのか。

こうした振る舞いを調べるため、20世紀の終わり頃に提案された、単純化した群れのモデル（Vicsek（ビチェック）モデル）をここでは紹介する。

まず、平面上に$N$個の粒子が分散している系を考える。粒子は、長さが1の「矢印」であると考え、$i$番目の座標を $\boldsymbol{r}_i$、矢印の方向ベクトル（長さは1）を$\boldsymbol{n}_i$で表す。そして、それぞれの粒子を動物に見立てて、矢印の方向に速さ $v_0$ で運動させる。

ゆらぎを伴った単独粒子の運動

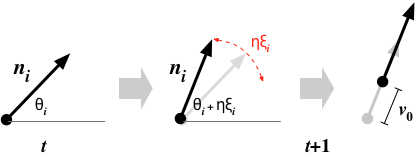
粒子の方向がふらふらと揺らいでいるような状況も想定して、$\boldsymbol{n}_i$ が時間的に変動する効果を取り入れる。時刻 $t$ での $\boldsymbol{n}_i$ の方向角を $\theta_i(t)$とすると、時間ステップ1ごとに方向角を $$ \theta_i(t+1) \leftarrow \theta_i(t) + \eta \xi_i \tag{1} $$ で更新する。ここで、$\xi_i$は、$[-\pi,\pi]$の範囲の一様乱数。 $\eta$が大きくなるほど、粒子は現在の向きを中心としたぶれが増すことになる。

そうして、時間1のあいだに $$ \begin{eqnarray} \boldsymbol{n}_i (t+1) & \leftarrow & (\cos(\theta_i(t+1)) , \sin(\theta_i(t+1)) ) \\ \boldsymbol{r}_i (t+1) & \leftarrow & \boldsymbol{r}_i (t) + v_0 \boldsymbol{n}_i(t+1) \end{eqnarray} \tag{2} $$ で位置と方向を更新する。

周囲と向きを揃える効果

粒子の現在の位置から半径 $R$ 内にある粒子の方向のベクトル和 $$ \bar{\boldsymbol{n}} = \sum_{\| \boldsymbol{r}_j - \boldsymbol{r}_i \| \lt R } \boldsymbol{n}_j \tag{3} $$ は、その領域内の粒子の平均的な方向を与える。そこで、時刻$t$での$\bar{\boldsymbol{n}}(t)$ の方向角を $\bar{\theta}_i(t)$として、(1)式の方向角の更新ルールを $$ \theta_i(t+1) \leftarrow \bar{\theta}_i(t) + \eta \xi_i \tag{4} $$ のように変更することで、粒子が互いに向きを揃える効果を表現する。近くの仲間の多数決で進行方向を決めるようなルールといって良い。

境界の影響

それぞれの粒子は(2)式に従って自走するため、（無限遠方から到来する粒子を考えない限り）いずれはどこか遠方に消え去ってしまうだろう。そこで、有限のサイズでモデルの振る舞いを調べるためには、この種の計算では周期境界条件を貸す場合が多い。矩形領域を考えると、右端と左端を「同じ辺」と考え、右端から飛び出した粒子は、左端から再び登場するようにしておけばよい。上下についても同様である。

近傍の探索

この種の計算では、近傍の粒子を調べる手間をできるだけ省く必要がある。全体で$N$個の粒子があるとすると、ある粒子から見て、半径$R$の円内に存在する粒子は全体のごく一部であるにもかかわらず、それを調べるために$N$回のチェック（距離計算）が必要となるのでは効率が悪い。そこで、空間を粗いマス目に区切り、それぞれのマス目にどの粒子が滞在しているかを登録しながら、計算を進めるとよい。そうすることで、近隣（上下、左右、斜め）のマス目に登録された粒子に対してだけ距離等の計算を行うだけで済むため、大きな$N$に対しても、効率の低下を減らすことができる。

以上を念頭に、$R=1$に固定した場合のVicsekモデルをコーディングした例を示す。ランダムさを表す$\eta$は、TwoDimFieldクラスのETA、 1ステップあたりの移動量（速度）を V0で与えるようになっている。

CやFortran等の機械語を生成するコンパイラ方式の言語に比べ、Pythonは実行速度が著しく遅いので、この種のシミュレーションにはあまり向いていない。ただし、まず、Pythonでモデルやアルゴリズムを検証し、C等に移植するのは生産的かもしれない。

実行にはpyglet(バージョン1.5.27以前）が必要

# coding: utf-8
# Yoshinori Hayakawa
# CDS, Tohoku University

import numpy as np
import random
import math
import pyglet
from pyglet.gl import *

class SDParticle:
    def __init__(self,L):
        x = random.random() * L
        y = random.random() * L
        nx = random.gauss(0,1)
        ny = random.gauss(0,1)
        d = math.sqrt(nx**2 + ny**2)
        nx /= d
        ny /= d
        self.update(x,y,nx,ny)

    def update(self,x,y,nx,ny):
        self.x = x
        self.y = y
        self.nx = nx
        self.ny = ny

class TwoDimField:
    V0=0.2
    ETA=0.2
    def __init__(self,L:int):
        self.L=L
        self.mesh = np.empty((L,L),dtype='object')
        self.list = [ ]
        self.epoch = 0

    def add_particle(self):
        a = SDParticle(self.L)
        ix = int(a.x)
        iy = int(a.y)
        if self.mesh[ix,iy]==None:
            self.mesh[ix,iy] = {a}
        else:
            self.mesh[ix,iy].add(a)
        self.list.append(a)

    def mod_L(self,x):
        if x<0:
            return x+self.L
        elif x>=self.L:
            return x-self.L
        else:
            return x

    def diff(self,d):
        if d > self.L/2:
            return self.L-d
        elif d < -self.L/2:
            return d + self.L
        else:
            return d

    def move(self,particle):
        ix = int(particle.x)
        iy = int(particle.y)
        sx = 0.0
        sy = 0.0
        for i in range(ix-1,ix+2,1):
            k = self.mod_L(i)
            for j in range(iy-1,iy+2,1):
                ell = self.mod_L(j)
                neighbors = self.mesh[k,ell]
                if neighbors == None:
                    continue
                for p in neighbors:
                    if self.diff(particle.x - p.x)**2 + self.diff(particle.y - p.y)**2 < 1.0:
                        sx += p.nx
                        sy += p.ny

        s=math.sqrt(sx**2+sy**2)
        sx /= s
        sy /= s
        xi = TwoDimField.ETA * random.uniform(-0.5*math.pi,0.5*math.pi)
        nx2 = sx * math.cos(xi) - sy * math.sin(xi)
        ny2 = sx * math.sin(xi) + sy * math.cos(xi) 

        x2 = self.mod_L(particle.x + nx2 * TwoDimField.V0)
        y2 = self.mod_L(particle.y + ny2 * TwoDimField.V0)
        if ix != int(x2) or iy != int(y2):
            self.mesh[ix,iy].remove(particle)
            if self.mesh[int(x2),int(y2)] == None:
                self.mesh[int(x2),int(y2)] = {particle}
            else:
                self.mesh[int(x2),int(y2)].add(particle)
        particle.update(x2,y2,nx2,ny2)

    def update(self):
        particle = random.choice(self.list)
        self.move(particle)
        dt = 1.0/len(self.list)
        self.epoch += dt

    def order_param(self):
        sx=0
        sy=0
        for p in self.list:
            sx += p.nx
            sy += p.ny
        return math.sqrt(sx**2+sy**2)/len(self.list)

###
L = 64
SCALE = 8
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(L*SCALE,L*SCALE,config=config,resizable=False)
win.set_caption('Vicsek Model')

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0,1)
    for particle in f.list:
        glColor3d(0.8,0.3,0.1)
        glLineWidth(SCALE/4)
        glBegin(GL_LINES)
        glVertex2d(particle.x*SCALE, particle.y*SCALE)
        glVertex2d(particle.x*SCALE + particle.nx*SCALE, particle.y*SCALE + particle.ny*SCALE)
        glEnd()

    str = 'T={0:.1f} Q={1:1.3f}'.format(f.epoch,f.order_param())
    label = pyglet.text.Label(str, 
                              font_name='Helvetica', color=(255,255,255,255),
                              font_size=12, x=10, y=10)
    label.draw()

def update(deltat):
    for cnt in range(1000):
        f.update()


f = TwoDimField(L)
for k in range(1000):
    f.add_particle()

pyglet.clock.schedule_interval(update, 1/20.0)
pyglet.app.run()

実行中の画面のスクリーンショット

Pygletバージョン2用のコード

Pygletはバージョン1と2とで仕様が変更になり、下位互換性が無い。以下に、バージョン2以上で動かすためのプログラムの例を示しておく。上に掲載したコードの ###以降を以下と置き換えればよい。画像ファイルを読み込むようにしているので、rod.png をダウンロードし、プログラムと同じフォルダに保存しておくこと。

実行にはPygletバージョン2以上、および画像データrod.pngが必要。

###
L = 128
SCALE = 8
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(L*SCALE,L*SCALE,config=config,resizable=False)

win.set_caption('Vicsek Model')

@win.event
def on_draw():
    glClear(GL_COLOR_BUFFER_BIT)
    glClearColor(0,0,0.2,1)
    redraw()

def next_frame(dt):
    return

def redraw():
    for cnt in range(N):
        f.update()
    for particle, rod in zip(f.list, rods):
        x0 = particle.x*SCALE
        y0 = particle.y*SCALE
        angle = math.atan2(particle.ny,particle.nx) * 180.0 / math.pi
        rod.x = x0
        rod.y = y0
        rod.rotation = -angle
        rod.scale = 0.025 * SCALE
        
    batch.draw()
    str = 'T={0:.1f} Q={1:1.3f}'.format(f.epoch,f.order_param())
    label = pyglet.text.Label(str, 
                              font_name='Helvetica', color=(255,255,255,255),
                              font_size=12, x=10, y=10)
    label.draw()


N =3000 # number of elements

f = TwoDimField(L)
for k in range(N):
    f.add_particle()

batch = pyglet.graphics.Batch()

rodimg = pyglet.image.load('rod.png')
rodimg.anchor_x = rodimg.width // 2 
rodimg.anchor_y = rodimg.height // 2

rods = [ ]
for particle in f.list:
    x0 = particle.x*SCALE
    y0 = particle.y*SCALE
    angle = math.atan2(particle.ny,particle.nx) * 180.0 / math.pi
    rod = pyglet.sprite.Sprite(img=rodimg, batch=batch)
    rod.x = x0
    rod.y = y0
    rod.rotation = -angle
    rod.scale = 0.025 * SCALE
    rods.append(rod)
    

pyglet.clock.schedule(next_frame)    

pyglet.app.run()

実行の様子（YouTube動画）

　発展練習：同期型アルゴリズムの実装

上のプログラムでは、$N$個の粒子の中からランダムに1つを選び、それをルールに従って動かす、という動作を繰り返すアルゴリズムを採用している。その点で、粒子の移動そのものにも揺らぎが伴っている。

そうではなく、式(3), (4), (2)に従って、全ての粒子が「同時に」移動するタイプのモデルに変更してみなさい。

相転移

一見、Vicsekモデルはとても単純に見えるが、全体としてどのように振る舞うかを予想することは困難である。粒子が全体として揃っているかどうかの量的な尺度として $$ Q = \frac{1}{N} \left\| \sum_i \boldsymbol{n}_i \right\| $$ がよく用いられている（秩序変数）。全体の向き完全に揃っている場合は$Q$は1に近く、ばらばらの場合はほぼ0となるような定義になっている。

矩形領域のサイズを$L$とすれば、その中の粒子の平均密度$\rho=N/L^2$と、ノイズの振れ幅 $\eta$ がこのモデルの重要なパラメータであり、 $\rho$と$\eta$に対して、上記の秩序変数がどのように依存するかが、このモデルが提案されて以来、久しく研究・議論されてきた。

理論的な予想は難しいので、実際にシミュレーションを行ってみてそれを予想することにならざるを得ないが、粒子数$N$やシステムのサイズ$L$、そして、実行時間が限られる中で、正しいと思われる答えにたどりつくには、何年も要することとなった。

　練習：秩序変数の変化

上記のコードでは、メイン部の変数Lが矩形領域の幅と高さ、そして、

f = TwoDimField(L)
for k in range(1000):
    f.add_particle()

の箇所のループの回数（ここでは1000）が粒子の数を決めている。

何通りかの$\rho$に対して、$\eta$を変えながら、秩序変数の変化の様子を調べ、横軸に$\eta$、縦軸に$Q$のグラフにまとめてみなさい。