Pythonプログラミング（モンテカルロ・シミュレーション）

細胞増殖のモンテカルロ・シミュレーション

このページでは、実験データ等の解析方法としてのモンテカルロ法の例を考える。

バクテリアの突然変異

20世紀の前半、遺伝物質としてDNAがまだ特定されていない頃、生物の突然変異はそれを誘導する因子が引き金になって生じるのか、あるいは、ランダムかつ自発的に生じるのか、よく分かっていなかった。 LuriaとDelbrückは、大腸菌と、大腸菌に寄生するウィルス（バクテリオファージ）を使った実験（「揺らぎ実験」として知られる）によって、この問題に定量的に答えてみせた。

ここでは、LuriaとDelbrückの揺らぎ実験を、コンピュータ上で再現してみたい。

大腸菌には、それに感染するバクテリオファージと呼ばれるウィルスがあって、ウィルスに感染すると、大腸菌は細胞が破壊され死滅する。そのため、ファージを含むような培地で菌を培養しても、大腸菌は増殖できない。ところが、まれにファージに耐性のある株が出現し、同じく耐性のある株に細胞分裂し増殖できることが知られている。大腸菌が生存・増殖しているかどうかは、バクテリアコロニーと呼ばれる斑点状のパターンによって確認することができる。

ランダムに変異が起こる場合のモデル

ここでは、ファージが存在しない環境で、$X$が細胞分裂の際に（一般に非常に小さな）確率$a$で突然変異して$Y$の「子」を生じる場合を考えよう。

ファージに耐性の無いバクテリアの細胞数を$X$、耐性のある細胞の数を$Y$とする。ここでは簡単のために、細胞は世代毎に倍加するものと仮定し、$n$世代目の細胞数をそれぞれ $X_n$、および$Y_n$と表記する。

$N$個に増殖したバクテリアのうちで、全くランダムに$k$個が変異体を生じるとすると、その確率は、$N$から確率$a$で$k$個を選ぶ場合の確率、すなわち二項分布 $$ P(k) = {N \choose k} a^k (1-a)^{N-k} $$ で表される。そして、$a$が小さい場合にこれはポアソン分布 $$ P(k) = \frac{\lambda^k e^{-\lambda}}{k!} $$ で近似できる（ここで$\lambda = a N$）。

一般に細胞数$N$は大きな数になるので、$\lambda = aN$が小さい数になるとは限らない。 $\lambda$が大きな場合、ポアソン分布は正規分布に漸近するので、実際上、$P(k)$を平均$a N$、分散$a N$の正規分布と見なすこともできる。重要なのは、揺らぎ（分散）が$N$に比例する点である。

Luriaらの論文では微分方程式を使って考察されているが、ここでは確率差分方程式で考えてみる。 $a$は、細胞分裂あたり生じる変異細胞の割合、と定義する。ひとつの細胞が分裂すると必ず2つの変異株を生じる場合は$a=1$となる。以下では、分裂は同期的に起こるという単純化をおこなっている。

$n$世代目の$X$細胞が倍加する過程で、そのうちの$\xi_n$個が突然変異するとし、突然変異した細胞は変異体のまま倍加するものとすると、細胞数の変化は漸化式 $$ \begin{eqnarray} X_{n+1} & = & 2 X_n - \xi_n\\ Y_{n+1} & = & 2 Y_n + \xi_n \end{eqnarray} $$ で表現することができる。ここで、$\xi_n$は、平均が$\lambda = 2 a X_n$となるようなポアソン分布に従う確率変数である。

上の２式を加えると $$ X_{n+1} + Y_{n+1} = 2 (X_n + Y_n) $$ であるから、細胞の総数は $$ X_{n+1} + Y_{n+1} = (X_0 + Y_0)\, 2^{n-1} $$ のように、単純に指数関数的に増加することは明らかであるが、$X_n$と$Y_n$のそれぞれは、確率的に大きく変動し、その様子を予想するのは簡単ではない。

単純化されたモデルで変異株の分布を求める試みは、Luriaらの論文が発表された後、あまり時間をおかずに成されたようで、その様子についてはこちらの総説などを参照のこと。

というのは、若い世代で突然変異が生じるかどうかで、その孫子が変異種になるかどうかが決まるため、サンプルごとに得られる$X$と$Y$の比率は、変異が生じるタイミングに依存して大きく揺らぐためである。下図では1個の$X$(白色の楕円）から出発した際、3世代目の$Y$（赤色の楕円）の数がサンプル毎に変動する様子を表現してみた。

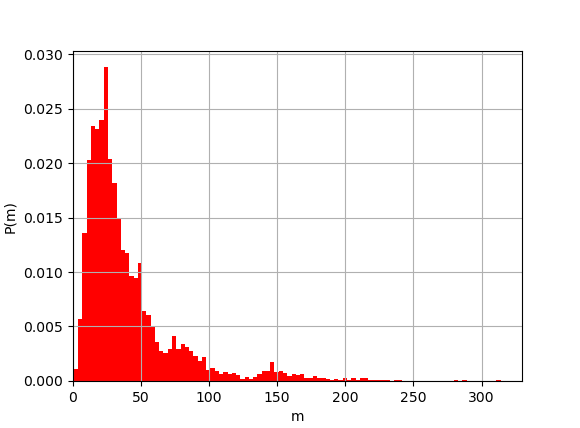
以下は、初期に$X$を1000000、$Y$は0個から出発して、8世代目の細胞数をシミュレーションするコードの例である。コードを実行すると、10000回分の試行を行い、最後に、$Y$の細胞数の平均と分散、そして頻度分布を表示する。

コード中で、ポアソン分布に従う乱数を発生は、NumPyライブラリを使って

import numpy as np
...
z = np.random.poisson(λ, 乱数の数)

のように行っている。すると、指定した個数の乱数がリスト（配列）として返される。

# coding: utf-8

import numpy as np
import matplotlib.pyplot as plt

a=0.00000002
ngen=8
ntrial=10000

mutant=[ ]

for _ in range(ntrial):
    x=1000000
    y=0
    for k in range(ngen):
        lam=2*a*x
        z=np.random.poisson(lam,1)
        x=2*x - z[0]
        y=2*y + z[0]
    mutant.append(y)

avr = np.mean(mutant)
var = np.var(mutant)

print("mean=",avr,"var=",var,"ratio=",var/avr)

plt.hist(mutant, bins=100, density=True, color=(1.0,0,0.0))
plt.xlabel('m')
plt.ylabel('P(m)')
plt.xlim(0)
plt.grid(True)
plt.show()

上のPythonコードの実行例。横軸が変異細胞の数、縦軸がその頻度。

結果を見ると、バクテリアが自発的かつランダムに変異すると仮定したモデルでは、変異した細胞数は大きく揺らいでおり、その分布関数は右側に長い裾野（テール）を持つことがわかる。詳しい解析によれば、この裾の部分は漸近的に $$ P(m) \propto m^{-2} $$ のようなべき乗関数で表されることがわかっている。

ファージによって変異が誘導されるモデル

他方、ファージによって変異が誘導されると仮定すると、ファージの無い環境では突然変異は生じないはずである。そこで、ファージを含まない環境で大腸菌を培養し、それをファージを含む培地に移してみる（下図）。ファージによって変異が誘導されるとすれば、移植した細胞数を$X$、移植から１世代後の変異細胞数を$k$とすれば、 $k$はポアソン分布 $$ P(k) = \frac{\lambda^k e^{-\lambda}}{k!} $$ で近似できるはずである。ここで$a$を変異が生じる確率として、$\lambda = a X$である。

右図の水色の四角の中では、図が煩雑になるため、変異体以外の細胞は省略した。

変異確率$a$は細胞毎に変わらないとしても、変異した細胞の数は移植した細胞数に依存するので、移植した細胞の絶対数がわからなければサンプル間の比較は難しいと思える。ところが、もし$k$がポアソン分布に従うとすると、その平均と分散は共に$\lambda$であるから、それらの比率を計算することで分布がポアソン的かどうかを確認することができる。

変異は自発的にランダムに生じるのか、あるいはファージによって誘導されるのか？

実際に、LuriaとDelbrück は上記のような実験を行い、変異細胞（コロニー）の数の統計量（平均と分散の比率）を吟味することによって、突然変異がファージによって誘導されたものではない（分布がポアソン的ではない）ことを明らかにした。すなわち、得られた変異細胞数のサンプルごとの揺らぎは、ポアソン分布のそれよりも明らかに有意に大きく、分裂過程で自発的に変異が生じたと考えざるを得ない。

突然変異が生じる頻度（パラメータ$a$）は非常に小さいが、実際にはどれくらいの大きさになっているか、実験的にはじめて見積もって見せたのもLuriaらである。推定にあたり、彼らは以下のような巧妙な方法を用いた：

$N$個のバクテリアが倍加して$2N$個に増殖した際に、$0$個の変異株が生じる（つまり変異が生じない）確率は $$ P(0) = \frac{\lambda^0 e^{-\lambda}}{0!} = e^{-2 a N} $$ である($a$は倍加後の細胞あたりの変異が生じる確率）。すると、$X_0$個から出発して、 $n$世代目までの倍加の過程で全く変異株が生じない確率は、世代ごとの確率の積 $$ p_0 = e^{-2 a X_0} e^{-2 a 2 X_0} e^{-2 a 2^2 X_0}\cdots e^{-2 a 2^{n-1} X_0} = e^{-2 a (2^n - 1) X_0} = e^{-2 a (X_n - X_0)} $$ となる（ここで、$X_n$は$n$世代目の細胞数）。

そこで、たくさんのサンプルを用意して、同じ世代（時間）だけ増殖した後でファージを加えた培地に移し、死滅しない細胞数（生じたバクテリアコロニーの数）をカウントし、 $$ p_0 =\frac{\textrm{コロニーが生じていないサンプルの数}}{\textrm{全てのサンプル数}} $$ によって$p_0$を求める。他方でサンプル中の最初の細胞数（$X_0$)と、培養後の細胞数（$X_n$)をカウントし、$p_0$の式に当てはめることによって、$a$を推定することができる。

ここで、コロニーの数（変異した細胞数）からは$a$を求めることはできないことに注意したい。というのは、変異した細胞数は変異がどの世代の倍加によって生じたのかに大きく依存する（揺らぐ）一方で、変異のタイミングを後から知る手立ては無いからである。ところが、変異が生じなかったサンプルについては、全ての世代で変異が無かったことが保証されているので、上記のような推定が可能となるわけだ。

　練習：適合度の検定

LuriaとDelbrückの論文("MUTATIONS OF BACTERIA FROM VIRUS SENSITIVITY TO VIRUS RESISTANCE", 1943)中のデータから、 10個のサンプル（Experimental No. 11)についてのファージ耐性を持った大腸菌の数を以下に転載した：

このデータがポアソン分布に従っていると考えられるかどうかを検定する方法を考え、それを実行してみなさい。