感染症拡大のパラメータ推定
このページでは、感染症拡大の様子をモンテカルロ法で推定する方法を考える。
乗算的な感染症の拡大過程
感染症が拡大する様子を考えてみよう。一人の感染者が複数にウィルス等を感染させ、 新しい感染者がまた複数に感染させるプロセスが繰り返されることによって「感染爆発」が生じる。 他方で、感染者があっても、周囲に感染させる率が十分低ければ、感染は終息する。
その様子を、 $n-1$ 日目に新規感染者が $X_{n-1}$ であったところが、$n$ 日目にはその $a_{n-1}$ 倍に増えて(あるいは減って) $$ X_{n} = a_{n-1} X_{n-1} \tag{1} $$ になるような過程として、表すことにしよう。 ここでの「倍率」$a_n$ は人々の暮らし方や政策に応じて日々変化していると考えられる。 1より大きければ指数関数的に感染が拡大し、1より小さければ急激に減少する。
0日目の感染者を$X_0$とすれば、$n$日目には $$ X_n = a_{n-1} \, a_{n-2} \cdots a_{0} \, X_0 \tag{2} $$ ということになる。両辺の対数を取って、 $$ Y_n = \log X_n $$ $$ b_n = \log a_n $$ と記号を変えれば、(2)式は $$ Y_n = b_{n-1} + \cdots + b_{0} + Y_0 \tag{3} $$ と書くことができる。
拡大倍率の系列($\{a_n\}$)、あるいはその対数($\{b_n\}$)は様々な要因によって確率的に変動すると考えられる。
拡大率と基本再生算数の関係
感性症の拡大の様子を表す重要なパラメータが基本再生産数$R$である。 感染者が1日あたりに新しい感染を引き起こす数を$\beta$、 感染者が回復するまでの平均日数の逆数を$\gamma$とすると、 $R = \beta/\gamma$ と定義される。
感染が拡大している最中を考えると、 $0$日目から起算して、$t$日後の感染者$I(t)$は $$ I(t) = I(0) \exp\left( \gamma (R -1) t \right) $$ のように指数関数的に増大することから、増大率の定義と見比べると $$ a = \exp\left( \gamma (R -1) \right) $$ あるいは $$ R = 1 + \frac{b}{\gamma} $$ という対応関係がある。
感染拡大率の確率的な推定
実際の計測(PCR検査や抗原検査)で、日毎の新規感染者数の系列が $\{x_0, x_1, \cdots, x_N\}$ のように得られたとしよう。 現実には、検査日と発症日は異なるし、市中には未発見の感染者も多数「隠れて」いるかもしれないが、ここでは簡単のため、それらは無視する。
また、それぞれのデータの対数を取った値を $\{y_0, y_1, \cdots, y_N\}$ と表記することにする。
ここで、得られたデータから、尤もらしい $\{a_n\}$ (あるいは$\{b_n\}$。ただし、$n=0,1,\cdots,N-1$) を推定する方法を考えてみよう。 なお、ここで述べる方法は、感染症の専門家のあいだで認められているものではなく、状況をひどく単純化した一例に過ぎない。
この場合、もし$\mu_n$が一定ならば、$X_n$は対数正規分布に従うことになる。
天下り的ではあるが、$y_n$の増分が、平均 $\mu_n$、分散 $\sigma^2$ の正規分布していると仮定してみる。 つまり、$y_n$は、前日の値からランダムに変動し、それが正規分布に従う、と理想化するわけである。 ここでは簡単のため、分散 $\sigma^2$ は日に依らず一定(ある定数)と仮定する。
するとその確率は、規格化定数を除けば、 $$ p(y_{n+1}, y_n | \mu_n) \propto \exp\left(- \frac{(y_{n+1} - y_n - \mu_n)^2}{2 \sigma^2} \right) \tag{4} $$ となる。
ここで、施策や人々の行動変容によって、$\mu_n$は日々変化しているであろう。 ただし、その前後の日で $\mu_n$ が大きく不連続的に変化することも考えにくい。 すなわち、$\mu_n$ 自体はある程度「なめらかに」変化すると想定できる。
そこで、$\mu$の増分が0を中心に正規分布するという風に、$\mu$ の事前確率に対して「拘束条件」を課しておくことにする。 $$ p(\mu_{n+1}, \mu_n) \propto \exp\left[ - \left( \mu_{n+1} - \mu_n\right)^2 \right] \tag{5} $$ 式から明らかなように、$\mu_n$の前後の値とのズレが大きい場合は事前確率が低くなるように調整される。
その上で、$\mu_n$ の尤度 $$ p(\{\mu_{n} \} | \{ y_{n+1} \}) = \frac{ p( \{ y_n \} | \, \{ \mu_{n} \} ) \; p( \{ \mu_{n} \} )}{p( \{ y_n \})} \tag{6} $$ をモンテカルロ法で推定してみよう。 $\mu_n$ ($b_n$ の最尤値)が推定できれば $n$ 日目の拡大率が評価できる。
このモデルは、見方を変えれば、「エネルギー」を $$ H = \sum_{n=0}^{N-1} \left[ \frac{(y_{n+1} - y_n - \mu_n)^2}{2 \sigma^2} + \left( \mu_{n+1} - \mu_n\right)^2 \right] \tag{7} $$ と置いたときの、「温度」1での $\{ \mu_n \}$ の状態を推定する問題とも言える。
メトロポリス法によるサンプリング
では、効率はひとまず度外視して、$\{ \mu_n \}$ の分布をメトロポリス法で推定してみよう。 サンプリングの仕方は自由度が大きいが、ここでは、$n$をひとつずつ均等に選びながら、状態を更新する方法を採ることにする:
- $\sigma$をある値にセット
- $\{\mu_n\}$の初期値をセット
- $n$ をランダムに選ぶ
- $p_0 = p(\mu_{n+1}, \mu_n, \mu_{n-1} | y_{n+1},y_n)$ を評価する
- 乱数 $\xi_n$ を発生させ、$\mu'_n \leftarrow \mu_n + \xi_n$ とおく
- $p_1 = p(\mu_{n+1}, \mu'_n, \mu_{n-1} | y_{n+1}, y_n)$ を評価する。
- $\alpha = \frac{p_1}{p_0} \gt 1$ ならば $\mu_n \leftarrow \mu'_n$ と置き直して、3から繰り返す(状態を更新)
- そうでなければ、$\alpha$の確率で $\mu_n \leftarrow \mu'_n$ と置き直して、3から繰り返す(状態を更新)
- 3から繰り返す(更新を棄却)
これを、初期状態に近い頃は除いて、$\{ \mu_n \}$ を「時々」サンプリングする操作を十分な回数繰り返せばよい。
Pythonによるコーディング
以下は、Pythonによるコーディングの例である。
この例では、2020年3月16日から5月9日までの、東京都の新型コロナウイルスの累積感染者数の時系列から、その増分として、毎日の新規感染者数の系列を得ている。 さらに、その5日間の移動 平均を求め、時系列の両端が除かれた 3月18日〜5月6日分 のデータの対数を取って、$\{y_n\}$ としている。
$\mu_n$の標準偏差 $\sigma$ を0.2、回復日数の逆数$\gamma$は0.2に設定し、最初の10000回は除いて、1000回サンプリングする。 そして、推定された日毎の$\mu_n$から再生算数$R$の変化をプロットしている。
# coding: utf-8
import math
import random
import numpy as np
import matplotlib.pyplot as plt
# 2020/3/16〜5/9の東京都の感染者数(累計)
x_cum =[
90,102,111,118,129,136,138,154,171,212,259,299,362,430,443,521,587,684,773,889,
1032,1115,1194,1338,1516,1703,1900,2066,2157,2316,2442,2590,2791,2972,3079,3181,3304,3436,3570,3731,3834,3906,3945,
4057,4104,4150,4315,4473,4564,4651,4709,4747,4770,4809,4845
]
max_nsamp=1000
sigma2 = 0.2**2
gamma = 0.2
x_cum = np.array(x_cum)
x = np.diff(x_cum)
# 5日分の移動平均
kernel = np.ones((5,))/5.0
xs = np.convolve(x, kernel, mode='valid')
y = np.log(xs)
mu = np.zeros((len(y)-1,))
mu_samp = np.zeros((len(y)-1,max_nsamp))
cnt=0
nsamp=0
while True:
k = random.randint(0,len(y)-2)
if k==0:
g0=math.exp(-(mu[k+1]-mu[k])**2)
if k<=len(y)-3:
g0=math.exp(-(mu[k+1]-mu[k])**2 - (mu[k]-mu[k-1])**2)
else:
g0=math.exp(-(mu[k]-mu[k-1])**2)
p0 = math.exp(-(y[k+1]-y[k]-mu[k])**2/sigma2)*g0
mu1 = mu[k] + random.gauss(0.0,0.1)
if k==0:
g1=math.exp(-(mu[k+1]-mu1)**2)
if k<=len(y)-3:
g1=math.exp(-(mu[k+1]-mu1)**2 - (mu1-mu[k-1])**2)
else:
g1=math.exp(-(mu1-mu[k-1])**2)
p1 = math.exp(-(y[k+1]-y[k]-mu1)**2/sigma2)*g1
alpha = p1/p0
if alpha > random.uniform(0.0,1.0):
mu[k] = mu1
cnt=cnt+1
if cnt>10000 and cnt%1000==0:
for k in range(len(y)-1):
mu_samp[k,nsamp] = mu[k]
nsamp=nsamp+1
if nsamp >= max_nsamp:
break
mean = np.mean(mu_samp,axis=1)
std = np.std(mu_samp,axis=1)
r = 1.0 + mean/gamma
r_std = std/gamma
days = range(0,len(y)-1)
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(days, xs[:-1], color=(0.0,1,0.0), linewidth=1.0)
ax2.errorbar(days, r, yerr=r_std, marker='o', color=(1.0,0.0,0.0), capthick=1, capsize=2, linewidth=0.5)
ax1.set_ylabel('N')
ax2.set_ylabel('R')
ax2.set_xlabel('DAYS')
ax1.grid(True)
ax2.grid(True)
plt.show()
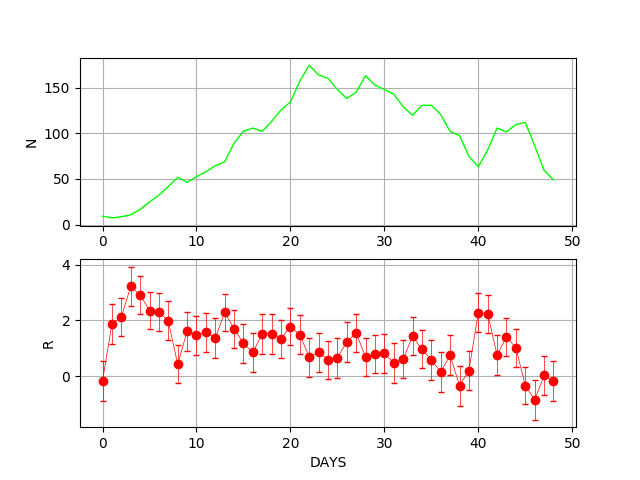
結果のプロットの例。 横軸は2020年3月18日からの日数。 上が東京都の新規患者数の5日間の移動平均。 下が$R$の推定値。 エラーバーは、サンプルされた$\mu_n$の標準偏差。 この場合、モデルで$\sigma$を一定としているので、それに近い値($\sigma/\gamma$)になっている。
実際の推定では、検査日と発症日のずれに加え、発症間隔(serial inverval)の分布等も考慮する必要があるだろう。
 解説: 確率的なプログラミング
解説: 確率的なプログラミング
ここで、上記のPythonコードの例を少し違った角度で考え直してみよう。
式(5) では、$\mu_n$の増分($d \mu_n$と表記する)が、平均0、標準偏差1の正規分布すると仮定している。すなわち $$ d \mu_n \sim N(0,1) $$ と表現できる。
$\mu_n$はその増分の累積なので、出発値を $\mu_0$ とすれば $$ \mu_n = \mu_0 + d \mu_0 + \cdots d \mu_{n-1} $$ となる。
一方で、式(4)では、$y_n$の増分( $d y_n$と表記する)が、平均 $\mu_n$, 標準偏差 $\sigma$ の正規分布すると仮定しているのだから $$ d y_n \sim N(\mu_n, \sigma^2) $$ と表現できる。そして、この$d y_n$ が観測量に対応する。
こうした確率モデルの様子を直接的に記述し実行するアプローチは、確率的プログラミングと呼ばれ、データ分析の現場でも広く使われている。 ここでは、その実装のひとつであるPyMC3を使ってコーディングした例を以下に示す。
コードの一部(モデル)は こちらのサイト の内容を参考に、改変・単純化したものです。
# coding: utf-8
import numpy as np
import pymc3 as pm
import theano.tensor as tt
# 2020/3/16〜5/9の東京都の感染者数(累計)
x_cum =[
90,102,111,118,129,136,138,154,171,212,259,299,362,430,443,521,587,684,773,889,
1032,1115,1194,1338,1516,1703,1900,2066,2157,2316,2442,2590,2791,2972,3079,3181,3304,3436,3570,3731,3834,3906,3945,
4057,4104,4150,4315,4473,4564,4651,4709,4747,4770,4809,4845
]
max_nsamp=1000
sigma2 = 1.0
gamma = 0.2
x_cum = np.array(x_cum)
x = np.diff(x_cum)
# 5日分の移動平均
kernel = np.ones((5,))/5.0
xs = np.convolve(x, kernel, mode='valid')
y = np.log(xs)
dy = np.diff(y)
model = pm.Model()
with model:
mu_0 = pm.Normal('mu_0', mu=0.0, sigma=0.5)
mu_steps = pm.Normal('mu_steps', shape=len(dy)-1)
dmus = tt.concatenate([[mu_0], mu_steps])
mus = pm.Deterministic('mus',dmus.cumsum())
dlog_cases = pm.Normal('dlog_cases', mu=mus, sigma=0.2, observed=dy)
trace = pm.sample(chains=1, tune=2000, draws=1000, target_accept=0.95)
pm.traceplot(trace)
Jupyter Notebookの使用を想定した場合、上記のコードの終了後に以下を実行すると、$R$の推定値がプロットできる:
import matplotlib.pyplot as plt
gamma = 0.2
r = np.mean(trace['mus'],axis=0)/gamma + 1
r_std = np.std(trace['mus'],axis=0)/gamma
days = range(0,len(dy))
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(days, xs[:-1], color=(0.0,1,0.0), linewidth=1.0)
ax2.errorbar(days, r, yerr=r_std, marker='o', color=(1.0,0.0,0.0), capthick=1, capsize=2, linewidth=0.5)
ax1.set_ylabel('N')
ax2.set_ylabel('R')
ax2.set_xlabel('DAYS')
ax1.grid(True)
ax2.grid(True)
plt.show()