最尤推定

このページでは、最尤推定についてあれこれ考える。

コイン投げ

偏りがあるコインを投げたところ、表をH、裏をTで表すことにして、$X=[H, T, T, H, T]$というデータの系列が得られたとしよう。 そのとき、そのコインの表の出る確率 $\theta$ を推定する方法を考えてみよう。

コイン投げの総数は5、表が出た回数は2であるから、すぐに$\theta=\frac{2}{5}$と答えが得られるだろうが、ここでは少し廻り道をして、考えてみたい。

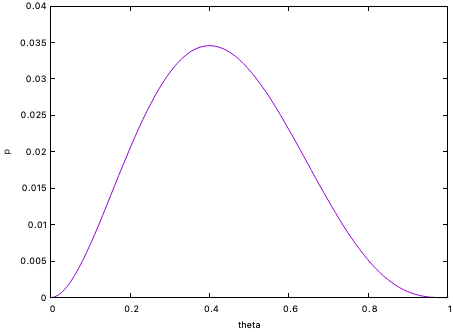
表が出る確率が$\theta$のコインを投げて、[H, T, T, H, T]が生じる確率は $$ p(X=[H, T, T, H, T]|\theta) = \theta \times (1-\theta) \times (1-\theta) \times \theta \times (1-\theta) = \theta^2 (1-\theta)^3 $$ である。 現に得られているデータから見て、もっとありそうな$\theta$の値の候補として、上の$p([H, T, T, H, T]|\theta)$を最大化するような$\theta$を考えるのは理にかなっているように思われる。 実際に、$(0,1)$の区間で $p([H, T, T, H, T]|\theta)$ を $\theta$ の関数としてプロットすると、上に凸な形状をしていることがわかる。

実際に微分をとって最大値を与える$\theta$を求めてみると $$ \frac{\partial}{\partial \theta} p(X=[H, T, T, H, T]|\theta) = 2 \theta (1-\theta)^3 - 3 \theta^2 (1-\theta)^2 = \theta (1-\theta)^2 (2 - 5 \theta) = 0 $$ とおいて $$ \theta = \frac{2}{5} $$ が得られる。

このように、データ$X$が与えられたとき、確率分布（この場合は二項分布）のパラメータ$\theta$の関数 $p(X|\theta)$を尤度と呼ぶ。 そして、尤度を最大化することによって、確率分布の母数（パラメータ）を点推定する方法が最尤推定（maximum likelihood estimate; MLE）法である。

　練習：ベルヌーイ試行の最尤推定

コインを$N$回投げて、表が$N_H$回、裏が$N-N_H$回現れるようなデータが得られた場合、$\theta$を最尤推定してみなさい。

ベイズ推定との関係

今度は、問題設定を変え、$\theta=1/2$と、$\theta=1/3$のコインが沢山入っている箱の中からランダムに１枚を取り出し、何回かそれを投げてみて、どちらのコインか推定してみよう。 $\theta=1/2$のコインの割合（すなわちそれを取り出す確率）を$p(\theta=1/2)$、$\theta=1/3$のそれを$p(\theta=1/3)$と表記する(この場合は$p(\theta=1/3) = 1 - p(\theta=1/2)$)。

すると、試行結果を知った上で$\theta=1/2$である可能性は、ベイズの公式から $$ p(\theta=1/2 | X ) = \frac{p(X|\theta=1/2) p(\theta=1/2)}{p(X|\theta=1/2) p(\theta=1/2) + p(X|\theta=1/3) p(\theta=1/3)} $$ となる。

これらを見比べると、最初に述べた尤度は、$\theta$の事前確率が一様分布している（可能性のあるコインを等しい確率で取り出した）ことを暗に前提していると解釈できる。 ベイズ統計学では、事前確率分布を仮定する根拠が見当たらない場合、可能な事象の確率は全て等しいと仮定するのが通例で、これは理由不十分の原理(principle of insufficient reason) と呼ばれている。

連続的な値を取るデータの尤度関数

連続値を取る$N$個のデータ $\boldsymbol{X} = [x_1, x_2, \cdots, x_N]$があって、それらが同じ確率的な過程で生成され、かつ、互いに独立であるような場合を考える。 ただし、どのような分布関数に従っているのかは未知であるとしよう。 それだけでは話しが始まらないので、ある母数$\theta$を持つ確率分布 $$ p(x|\theta) $$ をまず仮定する。 例えばガウス分布を仮定するときは、$\theta$は平均$\mu$と標準偏差$\sigma$を表す（すなわち$\theta =\{\mu,\sigma\}$)。

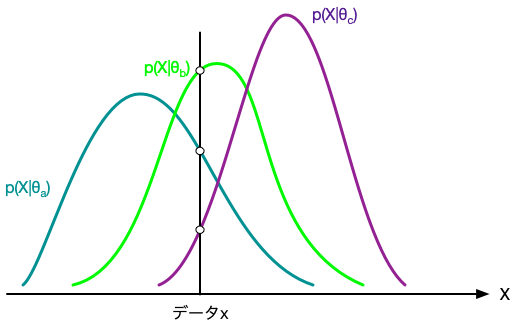
次に、データ$x_i$に照らして、パラメータ$\theta$の尤度として $$ p(x_i|\theta) $$ を採用することにする。 母数$\theta$を変化させると尤度も変化するが、尤度が大きいほど$\theta$がそのような値であったという確信の度合いも大きくなると考える。

上の尤度関数は確率密度関数と同じ形をしているが、$X$についての確率を議論しているわけではない点に注意が必要である。 $x$を幅$\Delta$で等分して、$k$番目の区画を$(k \Delta, (k+1)\Delta)$としてみる。 すると、データがその区間に見いだされる確率は $$ P\left(k \Delta \lt X \lt (k+1)\Delta \right) = \int_{k \Delta}^{(k+1)\Delta} p(x|\theta) dx $$ である。 いま、データ$x_i$が$k$番目の区画にあった場合に、パラメータ$\theta$の尤もらしさの指標として、上記の確率を採用するのは理にかなっているように思える。 ただし、そうすると、尤度は区画の幅$\Delta$のとり方に依存することになってしまう。 同じデータに対する尤度はユニークに定義されるべきであろう。

そこで、$\Delta \to 0$を取って、データ$x_i$に対する尤度を $$ \lim_{\Delta \to 0} \frac{P\left(x_i \lt X \lt x_i+\Delta\right)}{\Delta} = p(x_i|\theta) $$ で定義するのが都合がよい。

尤度はパラメータ$\theta$の関数であるが、パラメータは確率変数ではないので、尤度関数のパラメータの全空間での積分 $$ \int p(x|\theta) d \theta $$ は1である必要は無い。他方、 $$ \int p(x|\theta) dx = 1 $$ は必ず満足されていなければならない。

尤度の最大化

複数のデータ点が与えられた際に、それぞれが同じ確率分布に従う独立事象(iid)で生じたとすれば、すべてのデータについての尤度を、それぞれのデータについての積とするのが自然である。 $$ L(X|\theta) = \prod_{i=1}^N p(x_i|\theta) $$ そして、これを最大にするようなパラメータ（の組）が、データセットに照らして、いちばん尤もらしいと言えるだろう。

具体的な例として、平均$\mu$、標準偏差$\sigma$のガウス分布 $$ p(x | \mu, \sigma) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left[ - \frac{(x - \mu)^2}{2 \sigma^2} \right] $$ を考えてみよう。 $N$個の独立なデータに対する尤度は $$ L(X|\mu,\sigma) = \prod_{i=1}^N p(x_i|\mu,\sigma) = \frac{1}{(2 \pi \sigma^2)^{N/2}} \exp\left[- \frac{\sum_i (x_i - \mu)^2}{2 \sigma^2} \right] $$ となる。 対数関数は単調増加であるため、尤度の大小関係を比較する際には、尤度の対数(対数尤度）で議論する場合が多い。上記の場合の対数尤度は $$ \log L(X|\mu,\sigma) = - \frac{N}{2} \log (2 \pi) - \frac{N}{2} \log \sigma^2 - \frac{1}{2\sigma^2} \sum_{i=1}^N (x_i - \mu)^2 $$ である。

次に、（対数）尤度を最大にするようなパラメータを求めてみよう。 まず$\mu$について見てみると、対数尤度の式を眺めると $$ \sum_{i=1}^N (x_i - \mu)^2 $$ を最小にするような$\mu$が、尤度を最大にすることは明らかである（すなわち、$\mu$の最尤推定値は最小二乗法での結果に等しい）。 具体的には $$ \frac{\partial}{\partial \mu} \log L(X|\mu,\sigma) = 0 $$ を解いて、 $$ \mu^* = \frac{1}{N} \sum_{i=1}^{N} x_i \tag{1} $$ が得られる。すなわち、ガウス分布に対する平均の最尤推定量は、データの標本平均となる。

分散$\sigma^2$についても同様に $$ \frac{\partial}{\partial (\sigma^2)} \log L(X|\mu,\sigma) = 0 $$ と置いて解くと $$ {\sigma^2}^* = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu^*)^2 \tag{2} $$ となる。すなわち、標本分散が分散の最尤推定量となる。

このように、単純なガウス分布の場合にパラメータの最尤推定を行うことは容易であるが、一般の分布関数については、非線形方程式を解く必要が生じる。

　練習：ガウスモデルの最尤推定値

式(1)および式(2)が成り立つことを、具体的に対数尤度を偏微分して、確かめてみなさい。

　練習：ポアソン分布の最尤推定

離散的な非負の値$k$を取る確率変数をパラメータ$\lambda$のポアソン分布 $$ p(k|\lambda) = \frac{\lambda^k e^{-\lambda}}{k!} $$ でモデル化する場合を考える。

データセット $X = [k_1, k_2, \cdots, k_N]$ が得られた際の、パラメータ$\lambda$の最尤推定量を求めなさい。

正規乱数による「実証実験」

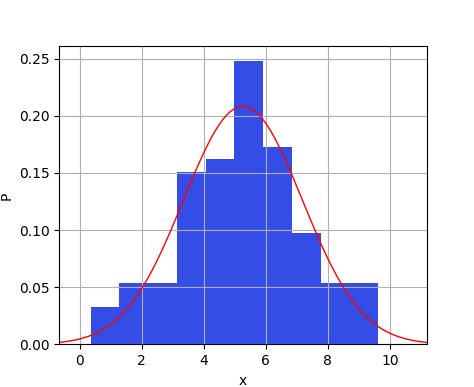
Pythonには疑似乱数を扱うモジュールが提供されているが、一様乱数だけでなく、いくつかの確率密度関数に従う乱数を発生させることができる。 以下は、SciyPyを使って、正規乱数の系列を発生させ、その平均と標準偏差を最尤推定で求めて、データのヒストグラムを推定された分布関数の両方をプロットするコードの例である。

# coding: utf-8
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import math

# 乱数発生
X = norm.rvs(loc=5, scale=2, size=100)
print('data=',X)

# 最尤推定
N = X.shape[0]
mu = sum(X)/N
print('mu=',mu)
V = np.sum(np.square(X))/N - mu**2
sigma = math.sqrt(V)
print('sigma=',sigma)

x = np.linspace(norm.ppf(0.001,loc=mu,scale=sigma), norm.ppf(0.999,loc=mu,scale=sigma), 100)

plt.hist(X,density=True,color=(0.2, 0.3, 0.9))
plt.plot(x,norm.pdf(x,loc=mu,scale=sigma),'-',color=(1.0,0,0.0),linewidth=1.0)
plt.xlim(min(x),max(x))
plt.xlabel('x')
plt.ylabel('P')
plt.grid(True)
plt.show()

　練習：ポアソン分布での実験

上記の正規乱数の例を参考に、ポアソン分布に従う乱数（非負の整数値）の系列を発生させ、そのパラメータを推定し、データのヒストグラムと推定された分布関数を表示するコードを作成してみなさい。

　ヒント

from scipy.stats import poisson
...
lam = 5.0
X = poisson.rvs(lam, size=100)