サンプリングによって先祖（親）の血液型を推定する

このページでは、家系図から親や先祖の血液型を推定する方法について考える。

母親の遺伝子型を推定する

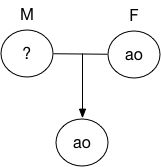
親子の血液型の遺伝を考えてみよう。 遺伝子型を小文字のa,b,oで表すことにした場合、 父親の血液の遺伝子型がaoで、その子の遺伝子型もaoであったとする。一方、母親の遺伝子型は不明であったとしよう。 既知の情報から、母親の血液の遺伝子型を推定するには、どのように考えるのが良いだろうか。

ここで、遺伝子型を$x,y$として、父親の遺伝子型を$\textrm{F:}xy$、母親を$\textrm{M:}xy$、子供を$\textrm{C:}xy$のように表すとする。 ベイズの公式によれば、母親の遺伝子型を$xy$とすると、 $$ P( \textrm{M:}xy, \textrm{F:ao} | \textrm{C:ao} ) = \frac{P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:ao}) P(\textrm{M:}xy) P(\textrm{F:ao})} {\sum_{x,y,w,z} P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:}wz) P(\textrm{M:}xy) P(\textrm{F:}wz)} $$ となるが、いま、父親と子供の遺伝子型は完全に分かっているのだから、 $$ P(\textrm{F:ao}) = P(\textrm{C:ao}) = 1 $$ で、それ以外の遺伝子型についての確率は0であるから($P(\textrm{F:aa})=P(\textrm{F:ab})=\cdots=0$)、 $$ P( \textrm{M:}xy, \textrm{F:ao} | \textrm{C:ao} ) = \frac{P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:ao}) P(\textrm{M:}xy)} {\sum_{x,y} P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:ao}) P(\textrm{M:}xy)} $$ となる。 すると、子供がao型、父親もao型で、かつ、母親の遺伝子型が$xy$である確率は $$ \begin{eqnarray} P( \textrm{M:}xy, \textrm{F:ao}, \textrm{C:ao} ) = P( \textrm{M:}xy, \textrm{F:ao} | \textrm{C:ao} ) P(\textrm{C:ao}) \\ = \frac{P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:ao}) P(\textrm{M:}xy)} {\sum_{x,y} P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:ao}) P(\textrm{M:}xy)} \end{eqnarray} $$ である。

実際に値を求めるには、確率分布 $P(xy)$ を知らねばならないが、ここで、日本人の 遺伝子型の比率(a: 0.28, b:0.17, o:0.55)を想定し、 ハーディー・ワインベルクの法則を仮定すると、 以下のコードで母親の遺伝子型毎の確率が計算できる：

# coding: utf-8

ptab = {'a': 0.28, 'b':0.17, 'o':0.55}

gt_ALL = ['aa','ao','ab','bb','bo','oo']

def pt(gt):
    x = gt[0]
    y = gt[1]
    if x==y:
        return ptab[x]*ptab[y]
    else:
        return 2*ptab[x]*ptab[y]

# P(C|M,F)
def pc(gt_c, gt_m, gt_f):
    gt=[ ]
    for c1 in gt_m:
        for c2 in gt_f:
            gt.append(''.join(sorted(c1+c2)))
    gt_c = ''.join(sorted(gt_c))
    n_match=0
    for c2 in gt:
        if c2 == gt_c:
            n_match += 1
    return n_match/len(gt)

# メイン部
for t_m in gt_ALL:
    psum=0
    for x in gt_ALL:
       psum += pc('ao',x,'ao')*pt(x)
    p = pc('ao', t_m, 'ao')*pt(t_m) / psum
    print(t_m,p)

血液型しかわからない場合

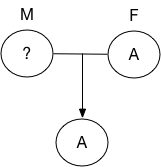
通常は、遺伝子型ではなくて血液型(A,B,AB,O)しかわからない。 そのような部分情報から、親（ここでは母）の血液型を推定する方法についても考えてみよう。

上図の例では、父親は aa, ao の可能性があり、他方、子供も aa, ao の可能性がある。 そうすると、母親は aa, ab, ao, bo, oo の可能性がある。

仮に、父親が aa で　母親が ao であれば、子供の遺伝子型が$xy$である確率は $$ P( \textrm{C:}xy | \textrm{M:ao}, \textrm{F:aa}) $$ 具体的には、子供が aa の確率は 1/2、aoである確率は 1/2である。

もし、父親が aa で子供が ao である場合は、母親が遺伝子型 $xy$ である確率は、前節のとおり $$ P( \textrm{M:}xy, \textrm{F:aa} | \textrm{C:ao} ) = \frac{P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:aa}) P(\textrm{M:}xy)} {\sum_{x,y} P( \textrm{C:ao} | \textrm{M:}xy, \textrm{F:aa}) P(\textrm{M:}xy)} $$ となる。 ここで、$P(\textrm{M:}xy)$ はハーディー・ワインベルクの法則によって与えるのが自然であろう。

今度は、もし母親が ao で、子供も ao であったとすると、父親の遺伝子型が$xy$である確率は $$ P( \textrm{M:ao}, \textrm{F:}xy | \textrm{C:ao} ) = \frac{P( \textrm{C:ao} | \textrm{M:ao}, \textrm{F:}xy) P(\textrm{F:}xy)} {\sum_{x,y} P( \textrm{C:ao} | \textrm{M:ao}, \textrm{F:}xy) P(\textrm{F:}xy)} $$ で与えられる。ここでも $P(\textrm{F:}xy)$はハーディー・ワインベルクの法則で決めることができるが、 実際に$xy$として許されるのは aa と ao のみである（父親の血液型がAであるから）。

このように、ある１人に着目すると、その「周り」の遺伝子型が既知であったとすれば、その人の遺伝子型の確率分布を推定するのは（式を計算する手間を除けば）容易である。

そこで、とりあえずの状態を設定しておいて、ある人に注目し、とりあえずの状態を元にして求めた確率に応じて、注目している人の状態を更新する作業を繰り返すようにする。 着目する人は順番に変えても、ランダムに決めてもよい（ただし、一様な重みでサンプルする必要がある）。すると、例えば、その状態は aa → aa → ao → aa → ... といった具合に目まぐるしく変化するはずである。

うまいことに、こうした更新作業を多数回繰り返すと、aaやaoの出現頻度は一定値に収束し、ちょうどそれぞれの遺伝子型の期待値（推定値）となることがわかっている。 このことは、父親と母親についても同様である。対象のうちのひとつ（ひとり）を選びながら、その状態を確率的に更新することで、知りたい量の期待値を得るこの方法は、 一般に、ギブスサンプリングと呼ばれている。

上記の手続きを100回繰り返すPythonコードの例を以下に示した：

# coding: utf-8

import random
import numpy as np

ptab = {'a': 0.28, 'b':0.17, 'o':0.55}

bt_A = ['aa','ao']
bt_AB = ['ab']
bt_B = ['bb','bo']
bt_O = ['oo']
gt_ALL = ['aa','ao','ab','bb','bo','oo']

def pt(gt):
    x = gt[0]
    y = gt[1]
    if x==y:
        return ptab[x]*ptab[y]
    else:
        return 2*ptab[x]*ptab[y]

# P(C|M,F)
def pc(gt_c, gt_m, gt_f):
    gt=[ ]
    for c1 in gt_m:
        for c2 in gt_f:
            gt.append(''.join(sorted(c1+c2)))
    gt_c = ''.join(sorted(gt_c))
    n_match=0
    for c2 in gt:
        if c2 == gt_c:
            n_match += 1
    return n_match/len(gt)

# P(M,F|C)
def pp(gt_m, gt_f, gt_c):
    psum=0
    for x in gt_ALL:
        for w in gt_ALL:
            psum += pc(gt_c,x,w)*pt(x)*pt(w)
    return pc(gt_c, gt_m, gt_f)*pt(gt_m)*pt(gt_f) / psum

def choose(choices):
    vtab=[]
    ktab=[]
    for k,v in choices.items():
        vtab.append(v)
        ktab.append(k)
    plist = np.array(vtab)/sum(vtab)
    return np.random.choice(ktab,p=plist)

# メイン部

state = {'M':'aa', 'F':'aa', 'C':'aa'}

for _ in range(100):
    # 母親を更新
    t_f = state['F']
    t_c = state['C']
    choices={ }
    for t_m in gt_ALL:
        choices[t_m] = pp(t_m, t_f, t_c)
    state['M'] = choose(choices)

    # 父親を更新
    t_m = state['M']
    t_c = state['C']
    choices={ }
    for t_f in bt_A:
        choices[t_f] = pp(t_m, t_f, t_c)
    state['F'] = choose(choices)

    # 子供を更新
    t_f = state['F']
    t_m = state['M']
    choices={ }
    for t_c in bt_A:
        choices[t_c] = pc(t_c, t_m, t_f)
    state['C'] = choose(choices)

    print(state)

　練習：ギブスサンプリングによる推定

上記のコードの例を出発点に、母親の血液型を推定し、確率として表示するコードを書いてみなさい。

　ヒント