混合ガウス分布によるデータのフィティング

このページでは、複数のガウス分布の重ね合わせでデータをフィッティングする方法を考える。

ガウス分布によるデータのフィッティング

コロイド粒子などの微粒子が、調和ポテンシャル中に閉じ込められてブラウン運動している場合、長い時間測定すると、その位置 $(x,y)$ の確率分布は $$ p(x,y) = \frac{1}{2 \pi \delta^2} \exp\left[ - \frac{(x-x_c)^2 + (y-y_c)^2}{2 \delta^2} \right] $$ のようにガウス分布する。 顕微鏡などで時事刻々と変化する粒子を長時間観察しながらその位置$(x_i, y_i)$を記録し、調和ポテンシャルの中心座標$(x_c, y_c)$と分布の広がり $\delta$ を推定したいとしよう。

対数尤度は $$ L(x_c,y_c,\delta) = - N \log(2 \pi) - N \log(\delta^2) - \sum_{i=1}^N \left\{ \frac{(x_i - x_c)^2 + (y_i - y_c)^2}{2\delta^2} \right\} $$ となるから、それを最大化するには $$ \frac{\partial L}{\partial x_c} = \sum_{i=1}^N \frac{(x_i - x_c)}{\delta^2} = \frac{1}{\delta^2} \left[ \sum_{i=1}^N x_i - N x_c \right] = 0 $$ $$ \frac{\partial L}{\partial y_c} = \sum_{i=1}^N \frac{(y_i - y_c)}{\delta^2} = \frac{1}{\delta^2} \left[ \sum_{i=1}^N y_i - N y_c \right] = 0 $$ $$ \frac{\partial L}{\partial (\delta^2)} = - \frac{N}{\delta^2} + \sum_{i=1}^N \left\{ \frac{(x_i - x_c)^2 + (y_i - y_c)^2}{2\delta^4} \right\} = 0 $$ これらは簡単に解くことができて、 $$ x_c = \frac{1}{N} \sum_{i=1}^N x_i $$ $$ y_c = \frac{1}{N} \sum_{i=1}^N y_i $$ $$ \delta^2 = \frac{1}{2 N} \sum_{i=1}^N \left\{ (x_i - x_c)^2 + (y_i - y_c)^2 \right\} $$ によって、ポテンシャルの中心位置と「広がり具合（ポテンシャルからの復元力と温度に依存）」が最尤推定できる。

２つのガウス分布を重ねたモデル

ここでは「目に見えない」２つのポテンシャル（番号1と2）があって、粒子はそのどちらかに捕捉（トラップ）されながら「行ったり来たり」 しているような状況を想定してみよう。そして、全体的な粒子の分布が単純に２つのガウス分布の重ね合わせ（混合） $$ p(x,y) = \frac{\alpha_1}{2 \pi {\delta_1}^2} \exp\left[ - \frac{(x-x_{c_1})^2 + (y-y_{c_1})^2}{2 {\delta_1}^2} \right] + \frac{\alpha_2}{2 \pi {\delta_2}^2} \exp\left[ - \frac{(x-x_{c_2})^2 + (y-y_{c_2})^2}{2 {\delta_2}^2} \right] $$ で表すことができると仮定する。 $\alpha_1, \alpha_2$はそれぞれのガウス分布の分配比率を表すパラメータで、$\alpha_1 + \alpha_2 = 1$。

このとき、粒子の位置データ $\{ (x_i, y_i) \}$ から、パラメータ $x_{c_1}, y_{c_1}, x_{c_2}, y_{c_2}, \delta_1, \delta_2$を推定するにはどのようにすれば良いだろうか。

それぞれのガウス分布を $$ p_k(x_i, y_i) = \frac{1}{2 \pi {\delta_k}^2} \exp\left[ - \frac{(x_i-x_{c_k})^2 + (y_i-y_{c_k})^2}{2 {\delta_k}^2} \right] $$ とおくと、対数尤度は $$ \begin{eqnarray} L & = & \log \prod_{i=1}^N \left( \alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i) \right) \\ & = & \sum_{i=1}^N \log \left( \alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i) \right) \end{eqnarray} $$ となるので、拘束条件 $G = \alpha_1 + \alpha_2 - 1 = 0$ の下で、これを最大化するようにパラメータを決めればよい。 ラグランジェの未定乗数を $\lambda$ とすれば、 $L + \lambda G$ を各パラメータで偏微分して0とおけばよい。

いくつか微分計算の例を示すと： $$ \begin{eqnarray} \frac{\partial (L + \lambda G)}{\partial x_{c_1}} = \sum_{i=1}^N \frac{\alpha_1}{\alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i)} \frac{\partial p_1(x_i,y_i)}{\partial x_{c_1}} \\ = -2 \sum_{i=1}^N \frac{\alpha_1 p_1(x_i,y_i)}{\alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i)} (x_i - x_{c_1}) = 0 \end{eqnarray} $$ $$ \frac{\partial (L + \lambda G)}{\partial ({\delta_1}^2)} = \sum_{i=1}^N \frac{\alpha_1 p_1(x_i,y_i)}{\alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i)} \left[ \frac{(x_i - x_{c_1})^2 + (y_i - y_{c_1})^2}{2 {\delta_1}^2} - 1 \right] = 0 $$ $$ \frac{\partial (L + \lambda G)}{\partial \alpha_1} = \sum_{i=1}^N \frac{p_1(x_i,y_i)}{\alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i)} + \lambda = 0 $$ となる。

ここで、$k=1,2$ それぞれに $$ w_{i,k} = \frac{\alpha_k p_k(x_i,y_i)}{\alpha_1 p_1(x_i,y_i) + \alpha_2 p_2(x_i,y_i)} $$ という「重み」を定義する。さらに $$ N_k = \sum_{i=1}^N w_{i,k} $$ と置くと、尤度を最大化する各パラメータは $$ x_{c_k} = \frac{1}{N_k} \sum_{i=1}^N w_{i,k} x_i $$ $$ y_{c_k} = \frac{1}{N_k} \sum_{i=1}^N w_{i,k} y_i $$ $$ {\delta_k}^2 = \frac{1}{N_k} \sum_{i=1}^N w_{i,k} \left[ \frac{(x_i - x_{c_k})^2 + (y_i - y_{c_k})^2}{2} \right] $$ $$ \alpha_k = \frac{N_k}{N_1 + N_2} $$ となる（拘束条件 $\alpha_1 + \alpha_2 = 1$ も用いると、$\lambda = -(N_1+N_2)$）。 式を眺めると、$w_{i,k}$ が与えられれば、データ$\{(x_i, y_i)\}$を使って尤度を最大化するパラメータが全て計算できることが判る。 ところが、$w_{i,k}$ の中身をよく見ると、パラメータが含まれているので、右辺から左辺が直接的に計算できるようにはなっていない点に注意が必要である。

推定アルゴリズム

前節の話しは、「堂々巡り」の構造をしている。つまり、パラメータ($x_{c_k}$や${\delta_k}$等)を最尤推定をするには $w_{i,k}$ が必要だけれども、 $w_{i,k}$ を計算するにはパラメータが必要である。 そこで、$w_{i,k}$ を隠れた変数と見なし、EMアルゴリズムを適用してみよう：

1. パラメータ$x_{c_k}, y_{c_k}, \delta_k, \alpha_k$ ($k=1,2$)にとりあえずの値を設定する
2. とりあえずのパラメータを使って、「重み」$w_{i,k}$ を求める
3. 計算した$w_{i,k}$を使って、パラメータを最尤推定する(最尤推定値を$x_{c_k}^*, y_{c_k}^*, \delta_k^*, \alpha_k^*$ ($k=1,2$)とする)
4. もし推定したパラメータが「前回」の推定値と「許容幅」以内であれば終了、そうでなければパラメータをステップ3での値に更新し、ステップ2から繰り返す

ここまでは、２つのガウス分布を混合した場合を考えたが、その数がさらに増えても同様の手続きが可能であるのは明らかであろう。 また、ここでは等方的な分布を考えたが、主軸が傾き歪んだ分布に拡張することもできる。

　練習：混合ガウス分布

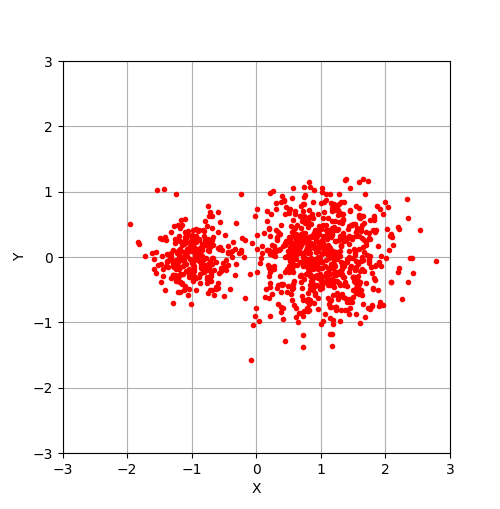
このページで説明したアルゴリズムをPythonで実装し、サンプルデータ(mixed-gaussian.dat)を読み込んで、パラメータを推定してみなさい。

　ヒント

# coding: utf-8

import math
import numpy as np
import matplotlib.pyplot as plt

file=open("mixed-gaussian.dat")
lines=file.readlines()
file.close()

xdata = []
ydata = []

for i in range(0,len(lines)):
    x,y=map(float,lines[i].split())
    xdata.append(x)
    ydata.append(y)

plt.plot(xdata,ydata, '.', color=(1.0,0,0.0))
plt.xlim(-3,3)
plt.ylim(-3,3)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()