Pythonプログラミング(ステップ9・クラスとオブジェクト・グラフの探索)
このページでは、オブジェクトを使った例として、ダイクストラ法を使ったグラフ上の最短経路探索について考える。
1.最短経路を探すアルゴリズム
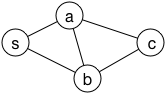
点 s から、いくつかの点(ここではa, bとしよう)まで道が伸びている。 ここで、s からそれぞれの点までの道のりを $d_{sa}$, $d_{sb}$と表すことにしよう。 もし、$d_{sa} \lt d_{sb}$ なら、sからaの最短経路はsからaへの道である。 つまり、sから直接到達できるうちで道のりが最短の点 a への最短経路は $s \to a$ で「確定」である。
ところが、sからbに直接延びる道は、sからbへの最短経路とは限らない。 なぜなら、sを出発後、aを経由してからbに至る経路のほうが短い(すなわち $d_{sb} \gt d_{sa} + d_{ab}$)かもしれないからだ。
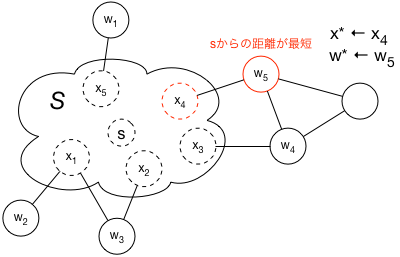
これと全く同じ考え方は、複数の点がある場合についても成り立つ。 sからの最短距離が既知の点の集合 $S$ があったとしよう。 それらの「既知」の点 $x$ $(\in S)$ に繋がっている点のうち、$S$には含まれない点 $w$ に注目する。 そして、出発点 $s$ から $x$ を経由して $w$ に至る道のり、すなわち $d_{sx} + d_{xw}$ が最も短くなるような $x, w$ の組を探し出し、それぞれ $x^*$, $w^*$ と表すことにしよう。
ここで、$d_{sx^*} + d_{x^* w^*}$ は $s$ から $w^*$ までの最短の道のりであることは明らかで、 $s \to \cdots \to x^* \to w^*$ 以外の $w^*$ に至る経路は $w^*$ への「廻り道」になる。 また、$w^*$は、$S$ に属する点を除けば、$x^*$からみて一番近い点である。
そうすると、この $w^*$ は、$s$からの最短距離が既知であるような点となったのだから、$S$ のメンバーに加えることができる (変数の「代入」に倣って $S \leftarrow S \cup \{ w^*\}$ と書くことにする)。
こうして、更新された $S$ に対して、再び、$s$からの道のりが最短となるような $S$ の隣接点を見つけ、$S$ に加える、という操作を繰り返せば、いずれ、全ての点について最短の道のりが(そして経路も)判明するはずだ。
上記の考え方に特段難しいところはないが、問題はむしろ、そんなに都合よく(簡単に)最短経路を与えるような $x^*, w^*$ が見つかるか、にある。 というのは、$S$ に 100 点が登録されていたとして、そこから道が繋がっていて $S$ には未登録な点が 100 ずつあったとすると、$100 \times 100$ 通りの組み合わせを試し、 その中から距離が最小のものを見つけ出さなくてはならない。 そういった作業を「既知」の点を加える度に行うのは、大変な工数である。
ここでひとつの妙案がある。以下で述べるように、$w^*$ を探す都度、途中経過を「道端」に残しておくと、格段に効率を上げることができる:
【隣接点へのメモ書き】
仮に, $x^*, w^*$ の組が見つかっているとしよう。 $w^*$ が $S$ に加わったとすると、$w^*$ から直接辿ることのできる点が、次のラウンドのチェックの対象として新たに加わることになる。 そこで、それを見越して、$w^*$ と繋がっている点のうち、$S$ には含まれない点に、そこまでの道のりを「メモ書き」しておくのだ。
$w^*$ に繋がっている点 $v$ $(\not\in S)$ までの道のりは $d_{sw^*} + d_{w^*v}$ となるが、 $v$ は $S$ に属する他の点とも繋がっている可能性があり、そちらを経由したほうが最短で辿り着ける可能性がある。 そこで、このメモ書きの際に、もし、$d_{sw^*} + d_{w^*v}$ よりも小さな値がすでに書き込まれていたらメモ書きするのは止めにする。 何もメモ書きが無い、あるいは、$d_{sw^*} + d_{w^*v}$ よりも大きな値が書き込まれていれば、その値を点 v にメモしておく。
【「確定点」の更新】
$w^*$ の隣接点へのメモ書きが終わったら、$w^*$ を新しく $S$ に加える。
【注目点を更新して反復】
次のラウンドの $w^*$ を見つけるには、$S$ には属さない点の中で、一番小さな数がメモ書きされたものを探せばよい。 そして新たに見つかった $w^*$ について、上記の手順を( $w^*$ が見つからなくなるまで)繰り返す。
【手続きの開始(出発)点】
すると、「一番最初の $w^*$」 が必要になるが、当然、それは出発点 s である。 s から s までの最短距離は 0 であるから、s に 0 をメモ書きしておいてから、上記の手続きを始めればよい。
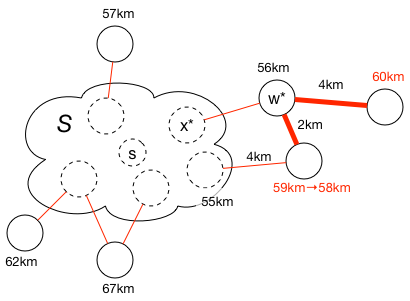
図:メモ書きの手順
メモ書きされた値が一番小さいの点 $w^*$ を見つける(図では56kmの点)。
そこから繋がっている(ただし$S$には含まれない)点までの道のりをメモ書きする(赤字)。
すでにメモ書きされている点については、 値を比較し、小さいほうの値を残す。
隣接する点のメモ書きが終わったら、$w^*$ を $S$ に加える。
上記のように途中結果をうまく活用すれば、『$x^*, w^*$を探索する作業』、は、『最小の値がメモ書きされている点を選ぶ』作業に置き換えることができ、 後者のほうが、圧倒的に要する工数が少なくできる。 この方法はダイクストラ法(Dijkstra's algorithm)と呼ばれるもので、 グラフ上の最短経路を探すアルゴリズムの定番である。 参考書 4.3節(p.121)にさらに詳しい説明が、 このアルゴリズムの「正しさ」の証明付きで掲載されているので参照のこと。
2.ダイクストラ法のコーディング
参考書に掲載されている道路網(図4.9)について、仙台から鹿児島までの経路を 上記のアルゴリズムで求めるPythonプログラムの例を以下に示す。 ここで、グラフ(ネットワーク)の表現には Graphというクラスと、その内部のVertexというクラスを用いている。 一見複雑なコードのように見えるが、最短距離(経路)の探索の処理はメイン部だけで行なわれており、 その他はグラフの作成と処理のための補助的なクラスと関数ばかりである。
クラス Vertex のメンバーのうち、
done はその点が確定済みかどうか(Falseは未確定)を、
distance はメモ書きされた距離(負の場合はまだメモ書きされていないこと)を、
route はひとつ「手前」の頂点、を、それぞれ表現するために使われている。
# coding: utf-8
import sys
class Graph:
"""a graph representation by Python """
class Vertex:
def __init__(self,name):
self.name=name
self.link=[ ] # list of [Vertex,weight]
self.distance=-1.0
self.done=False
self.route=None
def __init__(self):
self.vertices=[ ]
def create_vertex(self,name):
v = Graph.Vertex(name)
self.vertices.append(v)
def append_vertex(self,v, a, weight):
for x in v.link:
if x[0]==a.name:
v.link.remove(x)
break
v.link.append([a, weight])
def connect_vertex(self,v1, v2, weight):
self.append_vertex(v1,v2,weight)
self.append_vertex(v2,v1,weight)
def connect_vertex_by_number(self,n1,n2,weight):
try:
v1=self.vertices[n1]
v2=self.vertices[n2]
except:
return
self.connect_vertex(v1, v2, weight)
def print_link(self,v):
print(v.name,end="")
for x in v.link[n]:
print("-> ",x," ",end="")
print("")
def print_route_from(self,v):
x = v
while x is not None:
print(x.name," ",x.distance)
x = x.route
def init_graph(g):
g.create_vertex("Sendai") # 0
g.create_vertex("Fukushima")
g.create_vertex("Niigata")
g.create_vertex("Nagaoka")
g.create_vertex("Jouetsu")
g.create_vertex("Kanazawa") # 5
g.create_vertex("Nagano")
g.create_vertex("Takasaki")
g.create_vertex("Utsunomiya")
g.create_vertex("Mito")
g.create_vertex("Tsuruga") # 10
g.create_vertex("Shiojiri")
g.create_vertex("Koufu")
g.create_vertex("Hachiouji")
g.create_vertex("Ohmiya")
g.create_vertex("Tokyo") # 15
g.create_vertex("Chiba")
g.create_vertex("Maibara")
g.create_vertex("Nagoya")
g.create_vertex("Shizuyka")
g.create_vertex("Yokohama") # 20
g.create_vertex("Maizuru")
g.create_vertex("Kyoto")
g.create_vertex("Tsu")
g.create_vertex("Tottori")
g.create_vertex("Osaka") # 25
g.create_vertex("Nara")
g.create_vertex("Wakayama")
g.create_vertex("Matsue")
g.create_vertex("Hiroshima")
g.create_vertex("Okayama") # 30
g.create_vertex("Matsuyama")
g.create_vertex("Takamatsu")
g.create_vertex("Kouchi")
g.create_vertex("Shimonoseki")
g.create_vertex("Fukuoka") # 35
g.create_vertex("Hhita")
g.create_vertex("Nagasaki")
g.create_vertex("Kumamoto")
g.create_vertex("Kagoshima")
g.connect_vertex_by_number(0,1,81)
g.connect_vertex_by_number(0,2,220)
g.connect_vertex_by_number(1,3,240)
g.connect_vertex_by_number(1,8,172)
g.connect_vertex_by_number(1,9,202)
g.connect_vertex_by_number(2,3,62)
g.connect_vertex_by_number(2,4,132)
g.connect_vertex_by_number(3,4,80)
g.connect_vertex_by_number(3,7,171)
g.connect_vertex_by_number(4,5,185)
g.connect_vertex_by_number(4,6,89)
g.connect_vertex_by_number(5,6,230)
g.connect_vertex_by_number(5,10,136)
g.connect_vertex_by_number(6,7,120)
g.connect_vertex_by_number(6,11,85)
g.connect_vertex_by_number(7,8,103)
g.connect_vertex_by_number(7,13,104)
g.connect_vertex_by_number(7,14,109)
g.connect_vertex_by_number(8,9,80)
g.connect_vertex_by_number(8,14,95)
g.connect_vertex_by_number(9,16,150)
g.connect_vertex_by_number(10,17,54)
g.connect_vertex_by_number(10,21,78)
g.connect_vertex_by_number(10,22,98)
g.connect_vertex_by_number(11,12,85)
g.connect_vertex_by_number(11,18,205)
g.connect_vertex_by_number(12,13,118)
g.connect_vertex_by_number(12,19,115)
g.connect_vertex_by_number(13,15,48)
g.connect_vertex_by_number(13,20,58)
g.connect_vertex_by_number(14,15,34)
g.connect_vertex_by_number(15,16,41)
g.connect_vertex_by_number(15,20,34)
g.connect_vertex_by_number(17,18,70)
g.connect_vertex_by_number(17,22,83)
g.connect_vertex_by_number(18,19,182)
g.connect_vertex_by_number(18,23,81)
g.connect_vertex_by_number(19,20,165)
g.connect_vertex_by_number(21,22,110)
g.connect_vertex_by_number(21,24,170)
g.connect_vertex_by_number(22,25,51)
g.connect_vertex_by_number(22,26,40)
g.connect_vertex_by_number(23,27,183)
g.connect_vertex_by_number(24,25,188)
g.connect_vertex_by_number(24,28,120)
g.connect_vertex_by_number(24,30,140)
g.connect_vertex_by_number(25,26,35)
g.connect_vertex_by_number(25,27,80)
g.connect_vertex_by_number(25,30,175)
g.connect_vertex_by_number(26,27,99)
g.connect_vertex_by_number(28,29,170)
g.connect_vertex_by_number(28,34,312)
g.connect_vertex_by_number(29,30,161)
g.connect_vertex_by_number(29,31,85)
g.connect_vertex_by_number(29,34,200)
g.connect_vertex_by_number(30,32,45)
g.connect_vertex_by_number(31,32,160)
g.connect_vertex_by_number(31,33,130)
g.connect_vertex_by_number(32,33,130)
g.connect_vertex_by_number(34,35,100)
g.connect_vertex_by_number(35,36,160)
g.connect_vertex_by_number(35,37,152)
g.connect_vertex_by_number(35,38,113)
g.connect_vertex_by_number(36,39,350)
g.connect_vertex_by_number(38,39,175)
# メイン部
g = Graph()
init_graph(g)
# start from Sendai
g.vertices[0].distance = 0
while True:
dmin=sys.float_info.max
w=None
for v in g.vertices:
if v.done or v.distance < 0:
continue
if v.distance < dmin:
w=v
dmin = v.distance
if w is None: # if no more vertex to check then exit
break
for x,weight in w.link:
if not x.done:
if x.distance < 0:
x.distance = w.distance + weight
x.route = w
else:
if x.distance > w.distance + weight:
x.distance = w.distance + weight
x.route = w
w.done = True
# end of while
# Trace back from Kagoshima
g.print_route_from(g.vertices[39])
 練習:コードの改良
練習:コードの改良
上で示したコードの例では、反復の都度、全ての頂点について $S$ のメンバーかどうかやメモ書きされた道のりを調べている。 調べるべき点($S$には含まれず、メモが残されている点)の「管理簿」を別に用意して、その中の点だけをチェックする方式に改めてみなさい。