Pythonプログラミング(ステップ8・塩基配列のアラインメント)
このページでは、動的計画法の例として、二つの塩基配列の全体的な対応関係(グローバルアラインメント:global alignment)を調べる方法について考える。
1.塩基配列の整列(アラインメント)
生物のDNAやRNAの塩基配列や、アミノ酸の配列を比較しようとすると、案外と面倒な問題であることに気づく。例えば、異なる種の塩基配列(の一部)
配列1: ACCGT 配列2: ACG
はどの塩基同士が対応していて、全体として「どれくらい近い(遠い)」のだろう。
配列1が変異した結果配列2が生じた場合のみを考えても、いろいろな可能性が想定できるだろう。 例えば、三番目のCがGに置換され、GTが欠失したとみることもできるし、 2箇所の欠失が生じた結果、
配列1: ACCGT 配列2: AC-G-
となった、あるいは、別の場所で欠失が生じたもの
配列1: ACCGT 配列2: A-CG-
insertion and deletion = indel
と見なすことも可能である。
ここで - は挿入や欠失(インデルと呼ばれる)の結果生じたギャップを表している
(もちろん、塩基配列そのものにギャップ(隙間)が生じるわけではなく、対応する塩基を欠いている場所、の意)。
反対に、配列2を「元」とすれば、欠失箇所は挿入箇所へと解釈が変わる。
配列が長くなれば、解釈の可能性は膨大な数になるので、どのように変異が生じるかについて、ありそうな可能性を絞り込む必要がある。 そこで、配列のマッチングについて以下のような点数化を行なってみよう。
- 同じ種類の塩基がペアになっていれは $+s$点、異なっていれば$-s$点
- ギャップが1つ生じるごとに$-g$点
その上で、ペアの組み方を色々と変えて、スコアの合計が大きい配列(アラインメント)を選択すれば良さそうである。
実際の解析では、塩基ペアの一致と不一致でスコアを非対称にしたり、ギャッップの連続長に応じてペナルティを変化させたり (連続するギャップの生じにくさはギャップの長さに比例しない)など、もう少し複雑な配点ルールが用いられる場合もある。 また、アミノ酸配列のアラインメントを行う際は、20種のアミノ酸のペアごとに異なるスコアを割り当てた「スコア表」が用いられている(PAM250やBLOSUMなど)。
2.アライメントのスコア化
可能な全てのインデルのパターンそれぞれについて点数を計算しておいて、後から比較するのは、明らかに非効率である。 スコアの最も高くなるようなアラインメントを見つけるにはどうすればよいだろうか。
二つの塩基配列を $X = \{ x_1, x_2, \cdots, x_N\}$、$Y=\{ y_1, y_2, \cdots, y_M\}$と表現することにしよう。 $x_i$, $y_j$ のそれぞれは A, T, C, G のいずれかを表す。
ここで、$X$については$i$番目、$Y$については $j$番目のところまでの「部分鎖」(以下では$(i,j)$と表すことにする)についての、アラインメントの最大スコア(点数)を$H_{i,j}$と表記することにしよう。 スコアは、アライメントの整合性の程度を表す数値で、それが大きいほどふたつはよく一致していると解釈する。
そのときの部分鎖 $(i,j)$ は
- 部分鎖 $(i-1,j-1)$ に $X$と$Y$の塩基をそれぞれ追加:新たに塩基対を追加。
- 部分鎖 $(i-1,j)$ に $X$ の塩基を一つ追加:$Y$にギャップを挿入。
- 部分鎖 $(i,j-1)$ に $Y$ の塩基を一つ追加:$X$にギャップを挿入。
の3つの可能性のいずれかから生成される(両方の部分鎖にギャップを挿入する操作は考える必要はない)。
ここで、確定済みの部分鎖に対する最大スコアは、それ以降に塩基を継ぎ足しても影響されないことに注意しよう。 これは丁度、ダイクストラ法で最短経路を求める際に、確定済みの最短経路を「延長」する手続きに類似している。
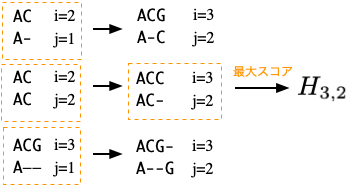
例:$(3,2)$アラインメントは、$(2,1)$, $(2,2)$, $(3,1)$ アラインメントから派生するが、その中で最大スコアとなるものを選ぶ。
すなわち、$(i,j)$アラインメントの最大スコア $H_{i,j}$ は、上記の3通りのやり方によってスコアの総計が最大となるもの、 式で表現すれば、 $$ H_{i,j} = \max \left\{ \begin{array}{c} H_{i-1,j-1} + s_{i,j} \\ H_{i-1,j} - g \\ H_{i,j-1} - g \end{array} \right. \tag{1} $$ のようにより短い部分鎖のスコアと関係づけることができる。 ここで、$g$はギャップひとつあたりのペナルティ、 $s_{i,j}$は、$x_i$と$y_i$の塩基対の点数である(同じ塩基ならば $+s$、そうでなければ$-s$点)。
ここで、境界条件は、$H_{0,0}=0$ とし、$H_{i,0}= H_{i-1,0} - g$, $H_{0,j}= H_{0,j-1} - g$ とする。
以上の関係は、再帰的な関数定義を使うことでごく自然に表現することができる:
import numpy as np
def get_score(i,j,x,y):
global H
if i<=0 or j<=0:
if i==0 and j==0:
H[i,j] = 0
elif i>0 and j==0:
H[i,j] = get_score(i-1,j,x,y)-2
elif i==0 and j>0:
H[i,j] = get_score(i,j-1,x,y)-2
return H[i,j]
else:
if H[i,j] >-1000:
return H[i,j]
else:
if x[i-1]==y[j-1]:
score=+1
else:
score=-1
H[i,j] = max([
get_score(i-1,j-1,x,y)+score,
get_score(i-1,j,x,y)-2,
get_score(i,j-1,x,y)-2
])
return H[i,j]
###
X = 'GGTTTATACCTTCCCAGGTAACAAACCAACCAACTTTCGATCTCTTGTAGATCTGTTCTCTAAACGAACTTTAAAATCTGTGTGGCTGTCACTCGGCTGC'
Y = 'ATTAAAGGTTTATACCTTCCCAGGTAACAAACCAACCAACTTTCGATCTCTTGTAGATCTGTTCTCTAAACGAACTTTAAAATCTGTGTGGCTGTCACTC'
N = len(X)
M = len(Y)
H = np.full((N+1,M+1), -1000, dtype='int16')
print('SCORE=',get_score(N,M,X,Y))
上のコードでは、Pythonの文字配列の添字が$0$から始まることから、式とは$s_{i,j}$の添字が1だけずれている点を除けば、式(1)をほぼ忠実に再現している。 なお、塩基対のスコアは $s=1$, ギャップのペナルティは $g=2$ としている。
このコードの例では、配列 H を用いたメモ化によって、計算効率を高める工夫をしているが、配列データが長くなると、関数の再起呼び出しが「深く」なりすぎてエラーとなってしまう。
 練習:トレースバック
練習:トレースバック
上記のコードを元にして、Yのインデルの場所にハイフンを入れて
ATTAA...GTGGCTGTCA-----CT-C
のように表示できるように改造してみなさい。
3.Needleman-Wunschアルゴリズム
本質的には前節のアルゴリズムと同じではあるが、関数の再起呼び出しを使わず、配列の操作のみで同様の計算を行うコードの例を以下に示す。 これは グローバルアラインメントの基本的な方法で、Needleman-Wunschアルゴリズムと呼ばれている。
$(i,j)$部分鎖のスコアを記録しておく配列Hと、状態遷移の「向き」を数値化して記憶しておく配列 L を用意し、
配列を「左上」から「右下」に向かって計算を進める。
$(i,j)$を参照する際に、$(i-1,j)$, $(i,j-1)$, $(i-1,j-1)$ のスコアが決まってさえいれば良いので、反復のしかたには自由度がある。
配列が全て埋まったら、L の内容を手がかりに、右下$(N,M)$から逆戻りすることで、スコアが最大となるアラインメントを得ることができる。
右のコードで使用しているサンプルデータ:
sequence-1.fasta
sequence-2.fasta
NCBIが公開している SARS-CoV-2ウィルスのRNAデータから使用。 全配列をアラインメントするには、記憶容量と計算時間からみて無理のため、右のコードでは、最初の100塩基のみを切り出している。
# coding: utf-8
import numpy as np
import sys
def read_fasta(name):
f = open(name, 'r')
seq=''
for line in f.readlines():
if line[0] != '>':
seq += line.strip()
f.close()
return seq
###
X = read_fasta('sequence-1.fasta')[0:100]
Y = read_fasta('sequence-2.fasta')[0:100]
N = len(X)
M = len(Y)
gap_penalty = -2
H = np.empty((N+1,M+1), dtype='int16')
L = np.zeros((N+1,M+1), dtype='int8')
H[0,0]=0
for j in range(1,M+1):
H[0,j] = H[0,j-1] + gap_penalty
L[0,j] = 0
for i in range(1,N+1):
H[i,0] = H[i-1,0] + gap_penalty
L[i,0] = 2
# Horizontal:0 Diagonal:1 Vertical:2
s = np.array([0,0,0],dtype='int')
for i in range(1,N+1):
for j in range (1,M+1):
s[0] = H[i,j-1] + gap_penalty
if X[i-1]==Y[j-1]:
score = +1
else:
score = -1
s[1] = H[i-1,j-1] + score
s[2] = H[i-1,j] + gap_penalty
H[i,j]=np.max(s)
L[i,j]=np.argmax(s)
pairs=[ ]
i=N
j=M
while i!=0 or j!=0:
if L[i,j]==0:
pairs.append( ["-",Y[j-1]] )
j=j-1
elif L[i,j]==1:
pairs.append( [X[i-1],Y[j-1]] )
i=i-1
j=j-1
else:
pairs.append( [X[i-1],"-"] )
i=i-1
pairs.reverse()
print('SCORE=', H[N,M])
for p in pairs:
print(p[0],end='')
print()
for p in pairs:
if p[0]==p[1]:
print('|',end='')
else:
print(' ',end='')
print()
for p in pairs:
print(p[1],end='')
print()
出力結果の例:
------GGTTTATACCTTCCCAGGTAACAAACCAACCAACTTTCGATCTCTTGTAGATCTGTTCTCTAAACGAACTTTAAAATCTGTGTGGCTGTCACTCGGCTGC
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| || |
ATTAAAGGTTTATACCTTCCCAGGTAACAAACCAACCAACTTTCGATCTCTTGTAGATCTGTTCTCTAAACGAACTTTAAAATCTGTGTGGCTGTCA-----CT-C
 解説: ライブラリの利用
解説: ライブラリの利用
塩基配列の操作に限らず、生物学に関係したデータ処理の多くはライブラリ化されているので、それらを使うのが簡単で確実である。 例えば、前節の例題プログラムを Biopythonを使って書き直した例を以下に示す:
# coding: utf-8
import numpy as np
from Bio import pairwise2
from Bio.pairwise2 import format_alignment
def read_fasta(name):
f = open(name, 'r')
seq=''
for line in f.readlines():
if line[0] != '>':
seq += line.strip()
f.close()
return seq
###
X = read_fasta('sequence-1.fasta')[0:100]
Y = read_fasta('sequence-2.fasta')[0:100]
alignments = pairwise2.align.globalms(X,Y,1,-1,-1,-1)
print(format_alignment(*alignments[0]))