Pythonプログラミング(ステップ8・関数・動的計画法)
このページでは、基本的に「総当り」で望むしか無いような組み合わせ問題を、なるべく効率的に解く方法について考える。
1.ナップサック問題
諸君は明日の遠足の準備をしているとしよう。ナップサックにお菓子を詰めているのだけれども、そこに詰められるのは2500グラムに制限されている。
手持ちのおやつや食品の重量と価値(値段)は以下の表の通りであったとしよう:
| 荷物の番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 重量(グラム) | 300 | 500 | 200 | 600 | 900 | 1360 | 800 | 250 |
| 価値(値段:円) | 400 | 250 | 980 | 340 | 670 | 780 | 570 | 800 |
重量の合計が2500グラム以内(2500グラムを含む)のとき、袋の中の荷物の価格の合計は、最大いくらにすることができるだろうか。
この問題をコンピュータに解かせるために、以下のステップで、アプローチしてみよう:
荷物のデータ表現
アルゴリズムの検討に入る前に、以下では、重量と価値の表を、Pythonのクラスとそのリストを使って、
class Item:
def __init__(self,w=0,p=0):
self.weight=w
self.price=p
items = [ Item(300,400), Item(500,250), Item(200,980),
Item(600,340), Item(900,670), Item(1360,780),
Item(800,570), Item(250,800) ]
と表現することにしよう。
こうして変数を定義しておけば、i番目の品の価値は items[i].price、重量は items[i].weight で得られる。
全ての組み合わせについて価値を調べる手順
基本的な考え方は、それぞれの荷物について、「入れる」、「入れない」を選びながら、重量の制約を満たすかどうか判定し、さらに、それらの中から価値の合計が最大になる組み合わせを見つける、ということになる。 その際に、$i$番目の荷物について「入れる」または「入れない」、$i+1$番目も「入れる」または「入れない」・・・という具合に、選択肢が枝分かれする「構造」がイメージできる。
ここで、0番目から始めて、$i$番目の荷物のパッキングをしている状況を想定してみよう。 以下では、$i$番目の荷物の重量を$w_i$、値段を$p_i$で表わすことにする。
仮に、$i$番目の荷物のパッキングをしている状況で、ナップサックにはまだ$w$グラム入れる余地があったする。 その状況で、ナップサックに入れることの出来る金額の最大値を与える関数 $knapsack(i,w)$ が与えられていたとしよう。 この関数を使うと、
- $i$番目の荷物を「入れない」場合、ナップサックの空きは変化せず、価値の変化も無いので、最大値は $i+1$番目以降のパッキングの結果 $knapsack(i+1,w)$ に等しい。
- $i$番目の荷物を「入れる」場合、ナップサックの空きは$w_i$だけ減少し、価格は$p_i$だけ増えるので、最大値は $i+1$番目以降のパッキングの結果と$i$番目の荷物の価格の和 $knapsack(i+1,w - w_i) + p_i$ に等しい。
以上のように「その先」のパッキングの最大値が評価できるとすれば、$i$番目の荷物を「入れない」場合と「入れる」場合の価値を比較し、 それらのうち大きい方を、$knapsack(i,w)$ の値(つまり$i$番目以降のパッキングの価値の最大値)とすればよい。
このアイデアを元に、関数の再帰呼び出しを使ってPythonのコードに翻訳した例を以下に示す:
knapsack.py
# coding: utf-8
class Item:
def __init__(self,w=0,p=0):
self.weight=w
self.price=p
items = [ Item(300,400), Item(500,250), Item(200,980),
Item(600,340), Item(900,670), Item(1360,780),
Item(800,570), Item(250,800) ]
def knapsack(i, w):
if i>=len(items):
return 0
elif w - items[i].weight < 0.0:
return knapsack(i+1, w)
else:
p1 = knapsack(i+1, w)
p2 = knapsack(i+1, w - items[i].weight) + items[i].price
if p1>p2:
return p1
else:
return p2
p = knapsack(0, 2500)
print("TOTAL PRICE=",p)
上の問題設定では、価格も重量も任意の値をとり得る。そのような場合に、ナップサック問題を解くうまい方法は知られておらず、基本的に「総当り」で調べる他ない。
 練習:パッキングの仕方
練習:パッキングの仕方
上のプログラムを修正して、価値が最大となるとき、何番目の荷物を入れればよいか、出力するようにしてみなさい。
階段の登り方
踊り場のない階段があったとしよう。 それを下から1段ずつ登るやり方は、もちろん、1通りしかない。 けれども、途中で1段飛ばしで(一度に2段)登るパターンを組み合わせて構わないとすると、色々な登り方のパターンが出てくる。 そのような場合、$n$段目まで登るやり方は何通りあるか、考えてみよう。
最初が0段目、として、1段目まで登るやり方は、当然1通り。それをここでは$f(1)=1$と表すことにしよう。 2段目まで登るやりかたは、『1段ずつ2回』と『2段一気に1回』の2通りあるから$f(2)=2$である。 $i$段目まで登るやり方も、『$i-1$段目から1段で』と『$i-2$段目から一気に2段』の2パターンあるから、これは漸化式 $$ f(i) = f(i-1) + f(i-2) $$ で表すことができる。 これは、これまで何度か登場したフィボナッチ数列そのもので、その解き方も幾つかのパターンが既に登場した。
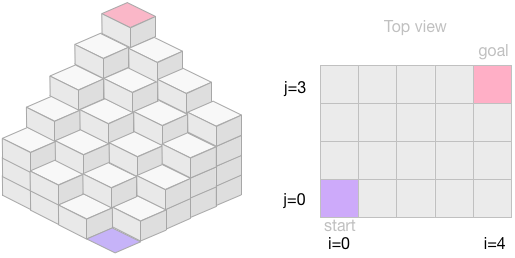
では、下図のような「二次元階段」の場合はどうだろうか。青(場所$(0,0)$)から出発して、$(i,j)$までたどり着く場合の数を$f(i,j)$とする。 ただし、この場合も、1段登ってもよいし、2段を一度に登っても構わないルールとしよう。
すると、場所$(i,j)$への登り方のパターンとしては $$ \begin{eqnarray} (i-1,j) \to (i,j) \\ (i-2,j) \to (i,j) \\ (i,j-1) \to (i,j) \\ (i,j-2) \to (i,j) \\ (i-1,j-1) \to (i,j) \end{eqnarray} $$ の5通りが考えられることになる(5番目の登り方はちょっと辛そうだが、気にしないことにしよう)。
この場合も「一次元階段」と全く同様の考え方ができて、漸化式 $$ f(i,j) = f(i-1,j) + f(i-2,j) + f(i,j-1) + f(i,j-2) + f(i-1,j-1) $$ を、初期条件 $$ f(1,0)=1, \,\, f(2,0)=2, \,\, f(0,1)=1, \,\, f(0,2)=2, \,\, f(1,1)=1 $$ のもとで計算すれば良い。 ただし、そもそも到達が不可能な領域についての境界条件 $$ f(i,j)=0 \; \textrm{for} \; i \lt 0 \; \textrm{or} \; j \lt 0 $$ も設定しておく必要がある。 これらの関係は、以下のように、そのままPythonの関数に翻訳できる:
def f(i,j):
if i<0 or j<0:
return 0
if i==1 and j==0:
return 1
elif i==2 and j==0:
return 2
elif i==0 and j==1:
return 1
elif i==0 and j==2:
return 2
elif i==1 and j==1:
return 1
else:
return f(i-1,j) + f(i-2,j) + f(i,j-1) + f(i,j-2) + f(i-1,j-1)
 練習:二次元階段
練習:二次元階段
上記のアルゴリズムに従って、$f(10,10)$ を評価するプログラムを作成し、動作を確認しなさい。
 ヒント
ヒント
上記の関数を使って「そのまま」計算できなくはないが、とても効率が悪い。 その主な理由は、再帰呼び出しの過程で、同じ$i,j$について、$f(i,j)$が繰り返し評価されるところにある。 そこで、
- 二次元のリスト(
table[[ ],[ ], ...]とする)を用意し、あらかじめ-1に初期化しておく。$i,j$の動作範囲に渡ってtable[i][j]にアクセスするに十分なサイズと用意しておく。
例えば、10✕10のリスト [ [-1,-1,-1,-1,-1,-1,-1,-1,-1,-1], [-1,-1,-1,-1,-1,-1,-1,-1,-1,-1], ...] を生成するには、Pythonの「リスト内包表記」を使って、以下のようにすればよい:table = [ [-1 for i in range(10)] for j in range(10)] - 関数$f(i,j)$を評価する際、もし
table[i][j]が-1ならば(その$i,j$の組については未評価なので)、上記の方法に沿って、値の計算を行ない、table[i][j]にその値を保存しておく。 - 関数$f(i,j)$を評価する際、もし
table[i][j]が-1でなければ(その$i,j$の組については既に評価済みなので)、return table[i][j];する。
という風に、途中結果を記憶しておく工夫(メモ化、memorizationと呼ばれる)をすると、計算効率を大きく改善することができる。
1次元階段問題の場合にメモ化を適用し、$f(40)$を評価するコードの例を以下に示す:
# coding:utf-8
def f(i):
if i==1:
return 1
elif i==2:
return 2
else:
if table[i]<0:
table[i]= f(i-1) + f(i-2)
return table[i]
# メイン部
table = [-1]*41
print(f(40))
 練習:整数ナップサック問題
練習:整数ナップサック問題
このページの最初に登場したナップサック問題で、荷物と価値の組み合わせが以下で与えられる場合について、 knapsack.pyを元に、メモ化の手法を使って効率化したPythonコードを作成しなさい 。ナップサックの容量(入れられる最大重量)は25とする。
| 荷物の番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 重量 | 3 | 5 | 2 | 6 | 9 | 13 | 8 | 3 |
| 価値 | 4 | 2 | 9 | 3 | 6 | 21 | 5 | 8 |
 ヒント
ヒント
関数 $knapsack(i,w)$の引数が動く範囲は、この場合、$i \le 7, \,\, w \le 25$ なので、途中結果を記憶するための配列のサイズは table[8][26] 分だけ確保しておけば十分。
問題の規模がさらに増え、品数が$n$, 容量(最大重量)が$C$になると、再利用のために結果を保管しておくには、最大 $n \times C$ 程度のメモリースペースが必要となる。