Pythonプログラミング（ステップ８・関数・あみだくじ）

このページでは、あみだくじを自動生成する方法について考える。

１．あみだくじ

隣り合った縦棒との間に横棒を水平に入れる、オーソドックスなあみだくじを考えてみよう。 あみだくじは、誰でも知っているように、どんな風に横棒を入れても、「出発点」と「終点」は必ず１対１に対応する。 異なる場所から始めたら、行き先が重複することは絶対にない。 出発点の縦棒の位置、左から右へ $1,2,\cdots,n$と番号をふって、$i$の行き先を行き先を$\sigma(i)$と表記することにすると、 この$\sigma$は置換(参考書のp.192）と呼ばれている写像になっていて、 出発点と終点の１対１対応は、『$\sigma$は全単射である』と言い換えることができる。

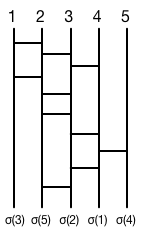
通常のあみだくじでは、横棒を「ランダム」に入れるので、置換（つまりくじの結果）は前もって不明であるが、ここではその逆（「やらせ」のくじ）を考えてみよう。 例えば、

$$ \begin{eqnarray}\left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 4 & 3 & 1 & 5 & 2\end{array}\right)\end{eqnarray} $$

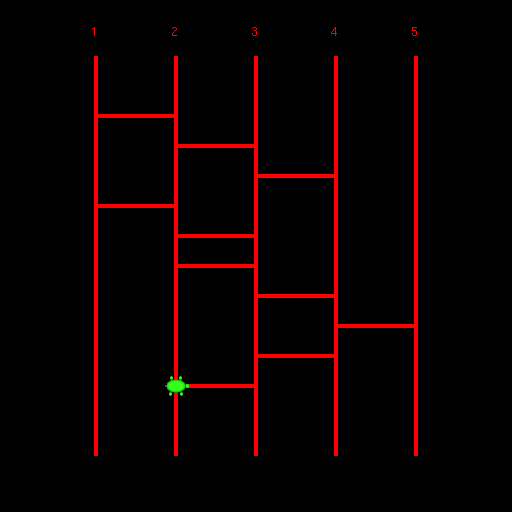
のように、置換を与えたときに、そうなるような横棒の位置を求め、具体的にそのくじ

を描けるようにしたい、というわけである。

２．置換を互換に分解する

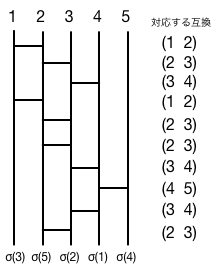
あみだくじの過程をよく考えると、横棒の箇所で、行き先が入れ替わっていることがすぐわかる。 つまり、横棒=隣同士の互換、という対応関係がある。 $i$番目の縦棒と$j$番目の入れ替えを$(i \;\; j)$と書くことにすると、上に示したくじの横棒と互換との対応は以下のようになる：

合成写像の書き方の慣習に倣って、置換は右から左に作用させる。



† ただし、互換の個数の偶奇は不変

つまり、あみだくじは、横棒を使って、与えられた置換を $$ (2\;\;3)(3\;\;4)(4\;\;5)(3\;\;4) (2\;\;3) (2\;\;3)(1\;\;2)(3\;\;4)(2\;\;3)(1\;\;2) $$ のように互換の積（合成写像）に分解して表現していることになる。 置換の分解方法には任意性があるので、もちろん、同じ結果が得られるようなあみだくじは、無限通り可能である†。 例えば上の例では$(2\;\;3) (2\;\;3)$の箇所があるが、これは「交換してすぐにまたもとに戻す」操作であるから、この部分の棒２本を除去しても、結果は変わらない。

あみだくじでは、『横棒はとなり同士の縦棒の行き先を交換する』という特徴がある。 つまり、互換の中に$(2\;\;5)$など、2つ以上離れた棒との交換が含まれないように分解を行う必要がある。

３．アルゴリズムとコーディング

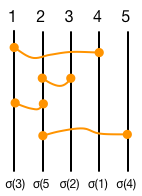
ここではまず、「隣同士」という制約が無い場合について、置換を互換の積に分解する手順から考えてみよう。 こうした問題を考える際、『ひとつずつ順に結果を確定させていく』方針が有効である場合が多い。 この問題の場合は、まず1の行き先が確定するように分解し、次いで2の行き先を確定させ、3、4・・、と同様の手順を進めていく、となる。

上記の$\sigma$ $$ \begin{eqnarray}\left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 4 & 3 & 1 & 5 & 2\end{array}\right)\end{eqnarray} $$ を左側から見ていくと、まず、1は4に写されるので $$L \leftarrow (1\;4)$$とおく。これで1の行き先が4に確定した。このとき4の行き先についてはひとまず気にしないでおく。

次に、2を3に写したい。ここで、前段階の置換$L$が作用し、1は4に、4は1に写された状態を考えなくてはならない。 2は$L$に影響されないので、$(2\;3)$を乗じて $$L \leftarrow (2\;3)\;(1\;4)$$とする。


 「隣同士を結ぶ」という制約がない場合のあみだくじ

続いて、3を1に写したい。ところが、ここまでの$L$で、3は2に写されているので、必要な入れ替えは$(2\;1)$となる（3→2→1）。 つまり、$$L \leftarrow (2\;1)\;(2\;3)\;(1\;4) $$

4を5に写す場合は、前段までに 4→1→2 と写されているので、$(2\;5)$を乗じて、 $$L \leftarrow (2\;5)\;(2\;1)\;(2\;3)\;(1\;4) $$

これで、1,2,3,4までの行き先が確定したので、自動的に5の行き先も確定していることになる。

それぞれの中間段階でも$L$が全単射であることには変わりが無いので、すでに確定した番号の行き先が、その他と「干渉」することは無い。

以上の考察から、$i-1$番目まで処理が終わっていて、$i$番目に進む過程は、形式的に $$ L_{i} \leftarrow \left(L_{i-1}(i)\; \sigma(i)\right)\circ L_{i-1} $$ とまとめられる。

この過程を素直にコーディングした例を以下に示す：

transposition.py

# coding: utf-8

def destination(L,i):
    s=i
    for x1,x2 in L:
        if x1==s:
            s=x2
        elif x2==s:
            s=x1
    return s


sigma={1:4, 2:3, 3:1, 4:5, 5:2}
L=[ ]

for i,c in sigma.items():
    j = destination(L,i)
    if j==c:
        continue
    L.append([j,c])

print(L)

ここでは、置換 $\sigma$ をPythonの辞書で、互換の積をリストのリストで表している。 $L$を表現する際に、例えば、$(2\;3)\;(1\;4)$ は [[1,4],[2,3]] に対応づけている(順序が反転している点に注意)。

destination(L,i) は、途中段階の置換によって$i$が写される先を求めるための関数である。

icon-pc　練習：あみだくじの自動生成

上記の例(transposition.py)を出発点に、置換が与えられたとき、それを「となり同士の交換」のみに分解し表示（すなわち、あみだくじの自動生成）するコードを作成してみなさい。

icon-hint　ヒント

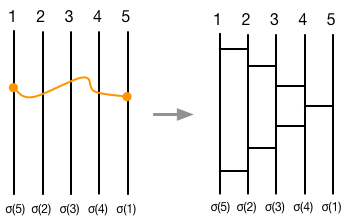
離れた縦棒の間での入れ替えは、隣同士の入れ替えの組にさらに分解して表現できるはずである。$(1\;5)$の場合の例を以下に示す。

例えば[1,5]を与えると、[[1,2],[2,3],[3,4],[4,5],[3,4],[2,3],[1,2]] を生成するような関数を定義してはどうだろうか？

コードが完成したら、さらに、より無駄の少ない横棒の構成法が無いかを考えてみるとよい。

tfield-icon亀場で練習：あみだくじの表示

亀場を使って、自動生成したあみだくじを表示するコードを作成してみなさい。