Pythonプログラミング（ステップ７・リスト・サンプリング定理）

このページでは、サンプリング定理について考える。

連続時間の離散的なサンプリング

我々にとっての時間は連続に流れているように感じられる。 そして、あらゆる現象もまた連続的に推移しており、いくらでも細かい時間の解像度で変化を調べることができそうに思える。 そのように、連続的な時間$t$とともに変化する量を$x(t)$とおくことにしよう。

その一方で、我々が計測可能なデータは、離散的な時刻毎での値である。 典型的には、一定時間間隔$T$毎の値として、 $$ x(t_0), \, x(t_0 + T), \, x(t_0 + 2 T), \, x(t_0 + 3 T), \cdots $$ が取得される。ここで、時間の原点をずらすことで、一般性を失うことなく、$t_0=0$と置くことができる。 こうして離散的な時刻で得られた系列は、元々の連続的なデータからどのくらい情報を失っているのだろうか？

同様の疑問は空間的なデータのサンプリングにおいても生じる。 たとえば、2Kの画像よりは4K、8Kの画像のほうが綺麗で美しいことは誰しも納得するだろうが、 もともとの映像がぼんやりとしか撮影されていなければ、いくら画面の解像度が高くても、違いは感じられないこともまた容易に想像できる。

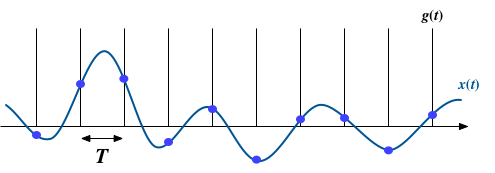
いま、データが間隔$T$の離散的な時刻毎($k=\cdots,-2,-1,0,1,2, \cdots$)に $$ x(k T) $$ のように与えられているとする。ここで、デルタ関数の列 $$ g(t) = \sum_k \delta(t - k T) \tag{1} $$ （櫛形であることから、Dirac combと呼ばれる）を考えると、間隔$T$毎に$x(t)$の値をサンプルしたパルス状の時系列を $$ x(t)g(t) = \sum_k x(t) \delta(t - k T) \tag{2} $$ と表現することができる。

一定時間毎のサンプリングしたデータの「波形」が $x(t) g(t)$ になるということではなく、積分 $$ \int x(t) g(t) \cdots dt $$ の評価が可能になる、という意味で、デルタ関数で表現すると何かと便利である。

$g(t)$は周期$T$の関数なので、フーリエ級数 $$ g(t) = \sum_n c_n e^{i \frac{2\pi n}{T} t} \tag{3} $$ で展開できる。そのフーリエ係数は、デルタ関数の性質と、積分区間に差し掛かるのは$k=0$の項のみであることに注意すると、 $$ c_n = \frac{1}{T} \int_{-\frac{1}{2T}}^{\frac{1}{2T}} g(t) \, e^{-i \frac{2\pi n}{T}} dt = 1/T \tag{4} $$ であるので、結局、 $$ g(t) = \frac{1}{T} \sum_n e^{i \frac{2\pi n}{T} t} \tag{5} $$ とも表すことができる。

そうすると、系列全体 $\{ x(k T) \}$ のフーリエ変換は $$ \begin{eqnarray} \tilde{X}(\omega) & = & \int_{-\infty}^{\infty} x(t) g(t) e^{-i \omega t} dt \\ & = & \frac{1}{T} \sum_n \int_{-\infty}^{\infty} x(t) \, e^{i \frac{2\pi n}{T} t} \, e^{-i \omega t} dt \\ & = & \frac{1}{T} \sum_n \int_{-\infty}^{\infty} x(t) \, e^{-i \left(\omega - \frac{2 \pi n}{T}\right) t} dt \\ & = & \frac{1}{T} \sum_n X\left(\omega - \frac{2 \pi n}{T}\right) \end{eqnarray} \tag{6} $$ と書くことができる。ここで$x(t)$のフーリエ変換を $$ X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-i \omega t} \, dt \tag{7} $$ と置いた。

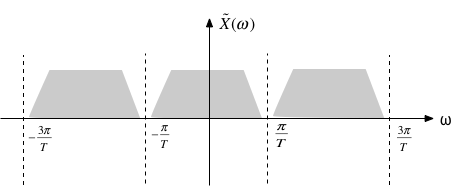
ここまでをまとめると、周期$T$でサンプリングした時系列のフーリエ変換は、「生」の信号のフーリエ変換を周波数軸でずらしながら重ねたものに等しい。

周波数領域での性質

ここで、もし、$X(\omega)$が、$-\frac{\pi}{T} \lt \omega \lt + \frac{\pi}{T}$ の範囲外の、高い振動成分を全く含まなかったとしよう。 すると（6)式の$n$についての和で、各項は「重なり」部分を全く生じないことになる。 そして、$-\frac{\pi}{T} \lt \omega \lt + \frac{\pi}{T}$ の範囲での $\tilde{X}(\omega)$は$X(\omega)$に完全に一致する。

このことは、$\tilde{X}(\omega)$を逆変換することで、元々の信号が完全に復元できること、 その意味で、何ら元の信号の情報は失われないことを意味する。

式（6)より、$\tilde{X}(\omega)$は$\omega$の空間で$\frac{2 \pi}{T}$の「周期」を持つので、これをフーリエ級数で $$ \hat{X}(\omega) = \sum_m d_m e^{i 2 \pi \frac{T}{2 \pi} \omega m} = \sum_m d_m e^{i T \omega m} \tag{8} $$ のように展開できる。ここで、展開係数は $$ d_m = \frac{T}{2 \pi} \int_{-\pi/T}^{\pi/T} \tilde{X}(\omega) e^{-i T \omega m} d\omega = \frac{T}{2 \pi} \int_{-\pi/T}^{\pi/T} X(\omega) e^{-i T \omega m} d\omega = x(-mT) \tag{9} $$ となる。

すると、$X(\omega)$の逆フーリエ変換は、$\tilde{X}(\omega)$のそれを用いて、以下のように完全に再構成できることが分かる： $$ \begin{eqnarray} x(t)& = &\frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega) e^{i \omega t} \, d\omega = \frac{1}{2\pi} \int_{-\pi/T}^{\pi/T} X(\omega) e^{i \omega t} \, d\omega = \frac{1}{2\pi} \int_{-\pi/T}^{\pi/T} \tilde{X}(\omega) e^{i \omega t} \, d\omega \\ & = & \frac{1}{2\pi} \int_{-\pi/T}^{\pi/T} \sum_k x(-kT) e^{i T \omega k} e^{i \omega t} \, d\omega \\ & = & \sum_k x(-k T) \frac{1}{2\pi} \int_{-\pi/T}^{\pi/T} e^{i (k T + t) \omega} \, d\omega \\ & = & \sum_k x(-k T) \frac{\sin(\pi (t + k T))}{\pi(t + kT)} = \sum_k x(k T) \frac{\sin(\pi (t - k T))}{\pi(t - kT)} \end{eqnarray} \tag{10} $$

以上をまとめると、元々の信号の持つ最大の各振動数を$\omega_{max}$とすると、 $2 \pi/T$がその倍以上になるようにサンプリング間隔$T$を選ぶと、 サンプリングしたデータ$\{x(kT)\}$のみを使って元の信号を完全に再現できる。

上式で、サンプリングを行った時刻のデータは、 $$ \lim_{t \to k T} \frac{\sin(\pi (t - k T))}{\pi(t - kT)} = 1 \tag{11} $$ であるから、当然ではあるが「そのまま」復元される。 サンプリングを行わなかった時刻でのデータも、上式による補間によって、完全に再現できることが保証される。