Pythonプログラミング(ステップ7・リスト・データの周期性)
このページでは、系列データの中の周期性の検出方法について考えてみる。
周期関数のテンプレート
以下では、簡単のため、データの平均は0と仮定する。そうでないデータの場合、全体から平均を差し引いておいてから考えればよい。
等しい間隔 $\Delta t$ 毎に得られた$N$個のデータ点(ここでは時系列を想定) $X_i$ $(i=0,\cdots,N-1)$ を考える。 言い換えれば、原点を0とすれば、$X_i$ は、時刻 $t_i = \Delta t \, i$ でのデータの値を表す。 もしもこのデータが角振動数 $\omega$ 周期関数によってに生成されたもの、すなわち、 $$ X(t) = A \sin( \hat{\omega} t ) + B \cos(\hat{\omega} t ) \tag{1} $$ であったとき、データ点から $\hat{\omega}$ や $A, B$ を知る方法について考えてみよう。
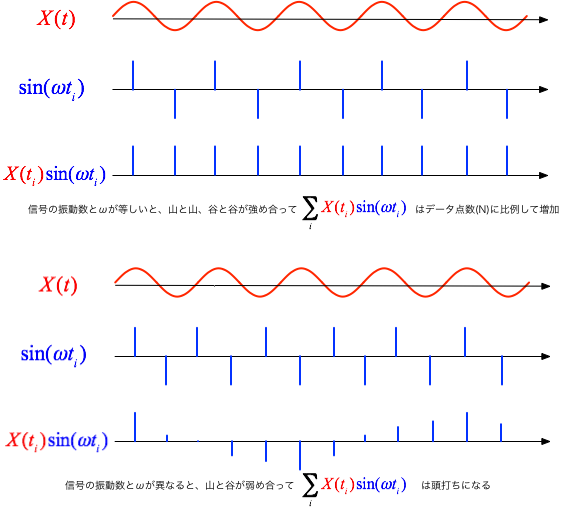
データ点は $$ X_i = A \sin( \hat{\omega} \, t_i) + B \cos( \hat{\omega} \, t_i ) \tag{2} $$ であるから、これに「テスト波形」$\sin( \omega t_i)$を乗じて和を取ると $$ \sum_i X_i \sin( \omega t_i) = \sum_i \frac{A}{2} \left[ \cos\left((\hat{\omega} - \omega) t_i\right) - \cos \left((\hat{\omega} + \omega) t_i\right) \right] + \sum_i \frac{B}{2} \left[ \sin\left((\hat{\omega} - \omega) t_i\right) + \sin \left((\hat{\omega} + \omega) t_i\right) \right] $$ となる。
ここで、$\sum_i \cos \left((\hat{\omega} + \omega) t_i\right)$ の挙動を考えると、交互に現れる山と谷の和が相殺するので、全体の総和は大きな値にはならない。 このことは、他の項についても同様である。
三角関数の総和が増大しないことの考察
ここで考えているのは $$ S = \sin(a) + \sin(a + b) + \sin(a + 2b) + \cdots + \sin(a+(N-1)b) $$ $$ C = \cos(a) + \cos(a + b) + \cos(a + 2b) + \cdots + \cos(a+(N-1)b) $$ の形の総和であることに注意しよう。 ここで、上記の議論は $a=0$, $b = (\hat{\omega} \pm \omega) \Delta t$ に対応している。
ここで、 $$ s = e^{a i} + e^{(a+b) i} + \cdots + e^{a+(N-1)b} $$ と置くと、オイラーの公式から、$S$と$C$はそれぞれ$s$の虚部と実部 $$ S = \Im(s), \, C=\Re(s) $$ であることがわかる。
$s$の式に等比級数の公式を適用すると $$ s = \frac{e^{ai} (e^{Nbi} -1)}{e^{bi} - 1} = \frac{\sin(Nb/2)}{\sin(b/2)} \exp\left[ \left(a + \frac{(N-1)b}{2} \right) i \right] $$ それぞれの実部と虚部から $$ S = \frac{\sin(Nb/2)}{\sin(b/2)} \sin\left(a + \frac{(N-1)b}{2} \right) \tag{3} $$ $$ C = \frac{\sin(Nb/2)}{\sin(b/2)} \cos\left(a + \frac{(N-1)b}{2} \right) \tag{4} $$ を得る。すなわち、三角関数の和は($b \to 0$の場合を除けば)$N$を増やしても必ず頭打ちとなる。
ところが、テスト波形の角振動数$\omega$が実際のそれにぴったり一致する場合だけは、$\cos\left((\hat{\omega} - \omega) t_i\right)$の項だけは常に1となる(山と山、谷と谷の位相が一致して強め合う)から $$ \sum_{i=0}^{N-1} X_i \sin( \hat{\omega} \, t_i) \approx \frac{A N}{2} \tag{5} $$ となる。 同様に、 $$ \sum_{i=0}^{N-1} X_i \cos( \hat{\omega} \, t_i) \approx \frac{B N}{2} \tag{6} $$
以上の考察から、時系列データから角振動数と振幅を推定するアルゴリズムとして、以下が考えられる:
- $\omega$を色々と変えながら以下の量を計算する:
- 振幅 $A$ を計算する:$$A = \frac{2}{N} \sum_i X_i \sin( \omega \, t_i) \tag{7}$$
- 振幅 $B$ を計算する:$$B = \frac{2}{N} \sum_i X_i \cos( \omega \, t_i) \tag{8}$$
- $A,B$が最大となる $\omega$ がデータの角振動数、$A,B$を振幅とする。
ここまでの考えは、元々の時系列が単一の角振動数のみで構成されていることを何ら前提にしていないので、 $$ X(t) = \sum_k A_k \sin( \hat{\omega}_k t ) + B_k \cos( \hat{\omega}_k t ) \tag{9} $$ のように、複数の波の重ね合わせであるような場合でも適用できる。 その場合は、複数の$\omega$で $A, B$に極大が観察されることになる。
周期と振幅の解析
上記のアルゴリズムを使って、東北電力が公開している東北・新潟地区の電力消費量の時系列データ(データはからダウンロードできる)の周期性を検出してみよう。 このデータはCSV形式で、データ点は1時間おきに与えられている。
時系列データをCSVファイルから読み込み、周期$T$を2時間から200時間まで1時間ずつ変え、$\omega = 2 \pi /T$ で積和によって、 振幅 $A, B$を算出、振幅の2乗 $A^2 + B^2$ をプロットするようにした例が下記のコードである。
データ: juyo_2018_tohoku.txt
# coding: utf-8
import pandas as pd
import math
import matplotlib.pyplot as plt
data = pd.read_csv('juyo_2018_tohoku.txt', encoding='Shift_JIS', skiprows=1)
date = data['DATE'].str.cat(data['TIME'],sep=" ")
datetime = pd.to_datetime(date,format='%Y/%m/%d %H:%M')
unixtime = datetime.map(pd.Timestamp.timestamp)
x = data['実績(万kW)'].tolist()
N = len(x)
AMP2 = [ ]
PERIOD = []
for period in range(2,200,1):
omega = 2*math.pi/period
s=0
c=0
for i in range(N):
s = s + math.sin(omega*i) * x[i]
c = c + math.cos(omega*i) * x[i]
AMP2.append( (s*2/N)**2 + (c*2/N)**2)
PERIOD.append(period)
plt.plot(PERIOD,AMP2, color=(1.0,0.0,0.0), linewidth=1.0)
plt.xlabel('PERIOD [HOURS]')
plt.ylabel('AMPLITUDE^2')
plt.grid(True)
plt.show()
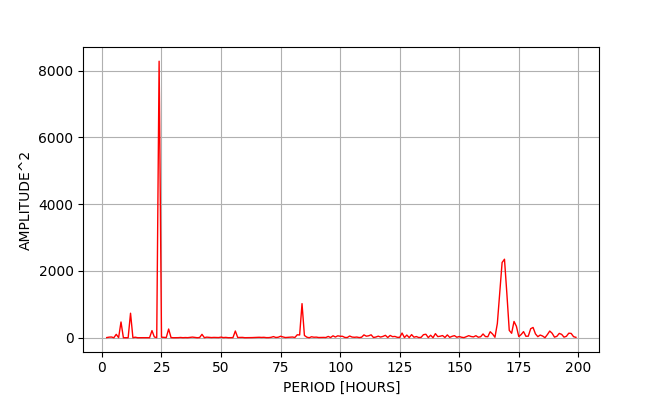
以下が解析結果のプロットで、横軸は周期(時間)、縦軸は振幅の2乗である。 明らかに24時間と1週間($24 \times 7 = 168$時間)付近にピークが現れているのが分かる。
実行結果
フーリエ変換とFFT
$N$点から成る時系列 $X_m$ に対する離散フーリエ変換を、次式で定義する($i$は虚数単位。これと記号が重複するので、添字に$m$を用いた): $$ Y_k = \sum_{m=0}^{N-1} X_m \exp\left(- 2 \pi i \frac{mk}{N} \right) \tag{10} $$ ここで、$k=0,1,\cdots,N-1$。 前節での振幅を求める式とよく見比べると、 $$ \omega = - \frac{2 \pi k}{\Delta t \, N} \tag{11} $$ と置くことで、 $$ Y_k = \frac{N}{2} B_\omega + \frac{N}{2} A_\omega i \tag{12} $$ という対応関係がある。すなわち、フーリエ変換とは、時系列データの、周波数毎の(複素数の)振幅情報への変換である。
ここで注意したいのは、(11)式のように、離散フーリエ変換では着目する角振動数を$\frac{2 \pi}{\Delta \, N}$の整数倍に限っている点である。 言い換えれば、振動の周期の整数倍が、必ず$N$点からなる区間にぴったりと一致するような場合のみを考えるわけである。 そして、フーリエ解析の理論によれば、周期$N$の関数は、そのような振動の重ね合わせによって表現できることが保証されている。
データ点が多くなると、全ての$k$(すなわち$\omega$)について $Y_k$を求めるためには、 乗算に着目すると、一つの$k$に対して、$N$回の乗算が必要となるので、全体で $N^2$回程度の計算量となる。 これは$N$が大きい場合、無視できない手間となる。
うまいことに、中間的な計算結果を巧妙に使い回すことによって、これを $N \log N$程度の計算量で済ませることができるアルゴリズムが知られており、 高速フーリエ変換(Fast Fourier Transform; FFT)と呼ばれている。 ここでは、FFTのアルゴリズムには立ち入らないで、NumPyに実装されているFFTを使った計算方法を紹介するに留める。
以下のコードは、NumPyのFFT関数を使って、時系列配列 x のフーリエ変換を求め、
それから、データの絶対値の二乗をプロットする例である。
# coding: utf-8
import pandas as pd
import math
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('juyo_2018_tohoku.txt', encoding='Shift_JIS', skiprows=1)
date = data['DATE'].str.cat(data['TIME'],sep=" ")
datetime = pd.to_datetime(date,format='%Y/%m/%d %H:%M')
unixtime = datetime.map(pd.Timestamp.timestamp)
x = data['実績(万kW)'].tolist()
N = len(x)
freq = np.linspace(0,1.0,N)
y = np.fft.fft(x, norm=None)
amp2 = np.absolute(y*2/N)**2
plt.plot(freq[10:N//2], amp2[10:N//2], color=(1.0,0.0,0.0), linewidth=1.0)
plt.xlabel('FREQ [1/HOUR]')
plt.ylabel('AMPLITUDE^2')
plt.grid(True)
plt.show()
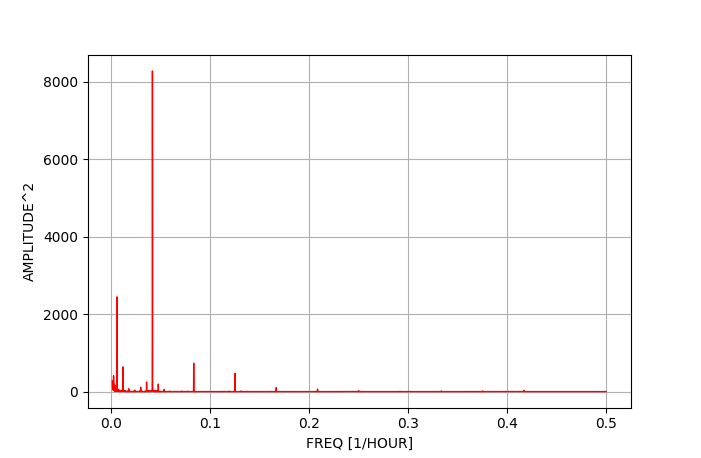
上記のコードを実行すると、横軸に周波数(1/時間)、縦軸のその周波数成分の振幅がプロットされる。 もっとも大きなピークは24時間、すなわち $1/24 \approx 0.041$ 付近に見られ、 次のピークは1週間、すなわち $1/(24 \times 7) \approx 0.0059$ 付近に現れていることがわかる。 また、それぞれの振幅も、前節で求めた結果と整合している。
実行結果
 解説: 離散フーリエ変換についての注意点
解説: 離散フーリエ変換についての注意点
データの前処理
分析の上で興味の無い、周波数が0およびそれに近い成分の振幅が相対的に大きいため、上記のコードでは$k$が10以上のデータ点のみをプロットしている。 データの周期的な挙動を抽出したい場合には、あらかじめ、各データ点から全体の平均値を差し引いて、周波数0の成分を取り除く等の前処理を行っておくと、そもそもDC成分は現れないし、計算精度の面でも有利である。
サンプリング間隔
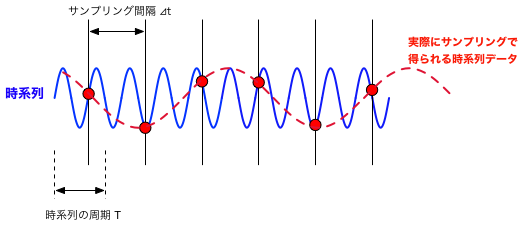
連続的な時間現象を、一定間隔 $\Delta t$ でサンプリングしてデータを取得する場合、サンプリング間隔よりも短い変動は当然検出することはできない。 (ナイキスト-シャノンの)サンプリング定理が教えるところによれば、正しく検出可能な周波数の上限を$f_c$とすれば、 $$ f_c = \frac{1}{2 \Delta t} $$ となる。 例えば、10Hzの現象を解析しようとすると、$\Delta t = 1/(2 \times 10) = 0.05$ 秒の以下の間隔(20Hz以上のサンプリング周波数)でデータを取得する必要がある。
高い周波数成分を持つ現象を、それには不十分なサンプリング速度で計測すると、折返し雑音と呼ばれる、本来は存在しない見かけ上の周期性が検知されてしまうので、注意が必要である。
周期$T$の時系列(周波数 $f=1/T$)を間隔$\Delta t$でサンプリングする際、 $\Delta t\gt \frac{T}{2}$であると、本来は存在しないはず周期の波が検出されてしまう。 これは、モアレ模様が「見える」原理と同じである。
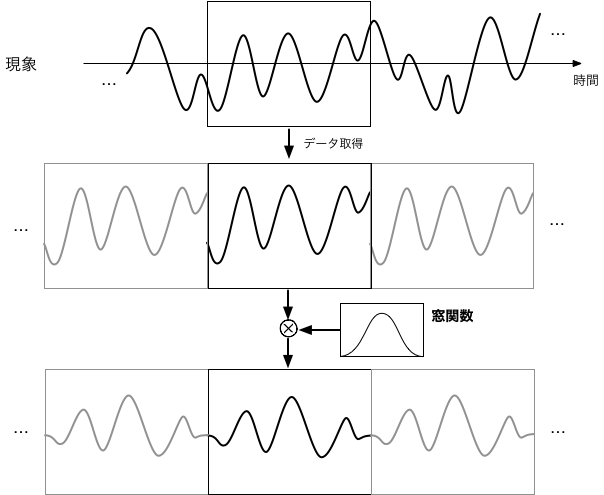
窓関数
離散フーリエ変換では、$N$個のデータ点が周期的に繰り返されているとの前提に立っている。ところが、実際のデータは現象の一部を切り出されたものなので、 それが繰り返されているとすると、データの両端で実際にはあり得ない「不整合」が生じる結果となる。 そして、この不連続性は、実際には存在しない振動成分として検出されてしまう。
そこで、窓関数と呼ばれる、両端でなめらかに零になるような関数とデータをかけて、両端が連続的に繋がるような前処理を行なっておく。 窓関数としては、細かな形状の違いにより、Hann窓、Hamming窓、Blackman窓などが用いられる。
以上を考慮して、若干手直ししたコードの例を示す:
# coding: utf-8
import pandas as pd
import math
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('juyo_2018_tohoku.txt', encoding='Shift_JIS', skiprows=1)
date = data['DATE'].str.cat(data['TIME'],sep=" ")
datetime = pd.to_datetime(date,format='%Y/%m/%d %H:%M')
unixtime = datetime.map(pd.Timestamp.timestamp)
x = data['実績(万kW)'].tolist()
N = len(x)
x0 = x - np.mean(x) # 直流成分除去
window = np.hanning(N) # Hann窓関数定義
ACF=1.63 # 振幅調整
x1 = (x0 * window) * ACF # 窓関数を適用
time = np.linspace(0,N,N)
freq = np.linspace(0,1.0,N)
y = np.fft.fft(x1, norm=None)
amp2 = np.absolute(y*2/N)**2
fig = plt.figure()
ax1 = fig.add_subplot(3, 1, 1)
ax2 = fig.add_subplot(3, 1, 2)
ax3 = fig.add_subplot(3, 1, 3)
ax1.plot(time, x0, color=(0.0,0.0,1.0), linewidth=0.2)
ax1.set_ylabel('10^4 KWH')
ax2.plot(time, x1, color=(0.0,0.0,1.0), linewidth=0.2)
ax2.set_xlabel('TIME [HOUR]')
ax2.set_ylabel('10^4 KWH')
ax3.plot(freq[0:N//2], amp2[0:N//2], color=(1.0,0.0,0.0), linewidth=1.0)
ax3.set_xlabel('FREQ [1/HOUR]')
ax3.set_ylabel('AMPLITUDE^2')
ax3.grid(True)
fig.tight_layout()
plt.show()
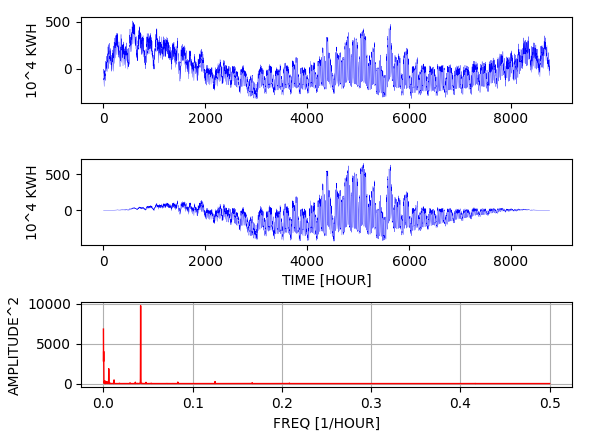
実行結果
上から、解析対象の時系列データ(電力消費量の推移)、窓関数を適用後の時系列、周波数と振幅の二乗の関係。